2020年高考山東卷圓錐曲線(xiàn)試題研究*

廣東省中山紀(jì)念中學(xué)(528454) 胡光裕 鞠火旺

一、呈現(xiàn)試題,分析求解

題目(2020年高考山東卷第22 題)已知橢圓C:的離心率為且過(guò)點(diǎn)A(2,1).

(Ⅰ)求C的方程;

(Ⅱ)點(diǎn)M,N在C上,且AM⊥AN,AD⊥MN,D為垂足.證明: 存在定點(diǎn)Q,使得|DQ|為定值.

本題考查了橢圓方程的求法,直線(xiàn)與橢圓的位置關(guān)系中直線(xiàn)過(guò)定點(diǎn)問(wèn)題,涉及到數(shù)形結(jié)合、分類(lèi)討論的思想;考查了學(xué)生的邏輯推理能力、轉(zhuǎn)化與化歸能力以及綜合運(yùn)算能力.

圖1

試題設(shè)置了兩問(wèn),梯度明顯,具有很好的區(qū)分度.第(Ⅰ)問(wèn)求橢圓方程,屬于常規(guī)問(wèn)題;第(Ⅱ)問(wèn)可謂“新瓶裝舊酒”,只要考生熟悉“手電筒”模型(過(guò)橢圓上一點(diǎn)A作AM⊥AN,直線(xiàn)AM、AN分別交橢圓于M,N兩點(diǎn)),則直線(xiàn)MN恒過(guò)定點(diǎn)P,又點(diǎn)A(2,1)是橢圓上的定點(diǎn),因此線(xiàn)段AP的長(zhǎng)度為定值.于是在RtΔADP中,中線(xiàn)QD的長(zhǎng)度等于斜邊AP的一半,因此滿(mǎn)足題目要求的定點(diǎn)Q存在,它就是斜邊的中點(diǎn).至此這道題就轉(zhuǎn)化為證明直線(xiàn)MN恒過(guò)定點(diǎn),這是本題的關(guān)鍵所在.

解(Ⅰ)C:過(guò)程從略.以下求解第(Ⅱ)問(wèn).

(1)若直線(xiàn)MN的斜率不存在,設(shè)其方程為x=x0,則M(x0,y0),N(x0,?y0),因?yàn)樗?x0?2,y0?1)·(x0?2,?y0?1)=0,即(x0?2)2+(1)=0,又代入解得或x0=2(舍),此時(shí)直線(xiàn)方程為x=

(2)若直線(xiàn)MN的斜率存在,設(shè)為y=kx+m,M(x1,y1),N(x2,y2),由得(1+2k2)x2+4kmx+2m2?6=0,由韋達(dá)定理又

故

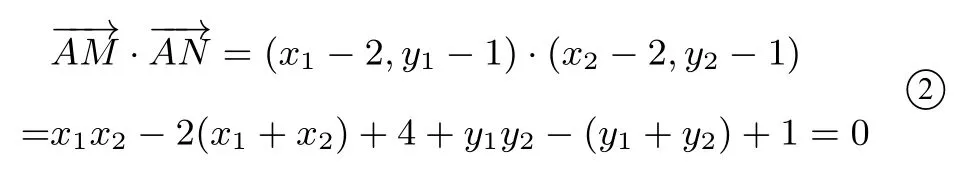
將①代入②得

又因?yàn)锳D⊥MN,D為垂足,所以ΔADP為直角三角形,且∠D為直角,因此當(dāng)點(diǎn)Q為斜邊AP的中點(diǎn)時(shí),|DQ|為定值,其值等于

二、推廣結(jié)論,揭示本質(zhì)

本題作為一道壓軸題,第二問(wèn)的本質(zhì)是考察直線(xiàn)MN過(guò)定點(diǎn).那么當(dāng)點(diǎn)A是橢圓上的任意一點(diǎn)且對(duì)于任意常數(shù)當(dāng)kAM ·kAN=δ時(shí),直線(xiàn)MN是否仍過(guò)定點(diǎn)呢? 如圖2 所示,在TⅠ-Nspire 中探究發(fā)現(xiàn)結(jié)論仍然成立,實(shí)際上,有如下的一般性的結(jié)論:

結(jié)論Ⅰ[2]已知點(diǎn)A(x0,y0)是……