一道高考題的7種解法

李昌成 李玉翠

(1.新疆烏魯木齊市第八中學 830002；2.新疆烏魯木齊市第64中學 830063)

近日在教學中遇到了一道老高考題，看起來很普通，細思極好，入口寬，解法多，是一個難得的高三復習素材.現分享于此，以饗讀者.

一、題目呈現

(2014年浙江省高考文科數學卷第16題) 若實數a，b，c滿足a+b+c=0，a2+b2+c2=1，則a的最大值為____.

二、總體分析

本題在代數背景下求最值，題設中有一次關系式，也有二次關系式，因此可以從方程、函數、一元二次不等式、均值不等式、解析幾何、三角代換等多角度思考此題.雖然這是一道高考題，但也可以用初中知識解答它.由此可見，本題起點低，構思巧，教學價值高.

三、解法探究

視角1 從已知的二次方程入手.

構造以a為參數，關于b或c的二次方程，利用一元二次方程有解的充要條件作答.

解法1 由a+b+c=0得b=-(a+c)①,

將①代入a2+b2+c2=1得a2+[-(a+c)]2+c2=1，

整理得2c2+2ac+(2a2-1)=0.

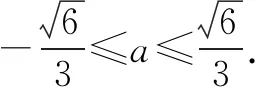
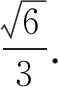
點評這種解法的關鍵在于消元，確定主元和參數.用一元二次方程有解的充要條件構造不等式.

視角2 從一元二次不等式入手.

通過消元，直接構造關于a的二次不等式，解不等式得a的最大值.

解法2 由a+b+c=0得b+c=-a，

由a2+b2+c2=1得b2+c2=1-a2.

因為b2+c2≥2bc，所以2(b2+c2)≥b2+2bc+c2，

即2(b2+c2)≥(b+c)2.

所以2(1-a2)≥(-a)2.

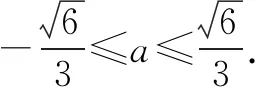
點評本解法結合題設的一次式、二次式的特征，通過運算，巧妙地徹底消元，同時構造了關于a的不等式.

視角3 從韋達定理入手.

將a看做參數，結合已知，通過推理運算用a表示b+c，bc，利用韋達定理構造一元二次方程作答.

解法3 由a+b+c=0得b+c=-a②,

將②平方得b2+c2=a2-2bc③,

將③代入a2+b2+c2=1得a2+a2-2bc=1，

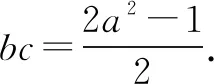
于是b，c是方程x2-(b+c)x+bc=0的實數解.

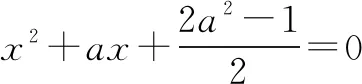
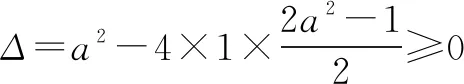
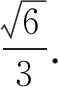
點評本解法在已知一次式的引導下，得到兩根之和；在韋達定理的引導下，通過……