中考視野下初中數學“一題一課”型復習課開展策略探究

蔡玉玲

摘要：從中考的角度，看初中數學復習課教學，教師要明確知道，其復習的目的不是讓學生會做這一道題，而是通過這一道題能夠得到學習能力的培養，能夠舉一反三，達到做一道題會一類題，真正發揮復習課開展的效益。為此，本文以提高學生解題效率，培養解題技能，提高數學學習能力為教學目標，從中考視野出發，針對初中數學“一題一課”復習課開展策略教學進行了探究分析。

關鍵詞：中考視野;初中數學;一題一課;復習課

中圖分類號：G633.6 文獻標識碼：A文章編號：1992-7711（2020）16-014-2

初中數學涉及理論、定義、性質、公式、幾何推導等多種類型的題型，期間各個知識點相互關聯，需要學生具備較強的思維能力和分析能力。面對中考，復習課如何上，如何開展，沒有固定的方式，但歸根結底，其根本目標是鞏固知識、提高能力，在復習中促使其能夠融會貫通，學會對問題進行分析、進行精準判定。而“一題一課”教學的開展就有效達到了這一教學目標，以一道題進行多種分析，構建多知識點，進行多角度變化，為數學學習支招，為問題解決添色，在突破思維定勢的基礎上，培養數學學習能力，達到有效教學。

一、原題展示——學會提問

對于復習課教學而言，要想讓學生達到舉一反三的學習效果，教師就要讓學生針對問題進行提問，在觀察問題的過程中，生成新的知識點，讓學生能夠自主設置問題，自主思考，在主動探索中，成為課堂學習的主人。以此來完善數學復習課教學過程，提高教學質量，在原題展示中與學生進行互動溝通，在原題觀察中突破思維定勢，以問題的形式進行解析、探索、生成、創新，最終實現學生數學思維能力的培養。例如，教師出示以下問題：

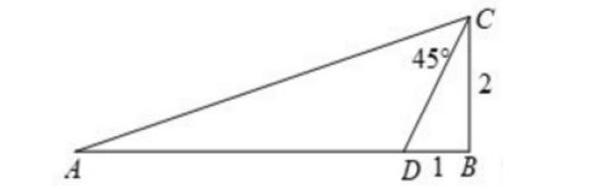
在Rt△ABC中，∠B=90°，BC=2，點D是AB上的一點，鏈接CD，已知BD=1，∠ACD=45°

通過問題的設計，與學生進行以下交談，

師：在這個問題中，已知的量有哪些？通過已知的量和圖形的觀察，你能發現哪些問題需要解決？涉及到哪些數學知識點？

生1：有45°角，可以聯想到勾股定理知識點。

生2：給出了BC、BD等邊長，那么可以生成“求AC邊的長”數學問題。

生3：我認為，在所有三角形中問題中，運用最多、最普遍的有三角形相似、三角形全等、銳角三角函數等知識點。

通過師生交談，激活思維，進行問題創編解決，在這一過程中，為提高學生解題效率和解題質量，在問題生成解決之前，教師可以讓學生結合自己所聯想到的數學知識點進行知識鞏固，如勾股定理的公式a2+b2=c2，等面積思想;相似三角形判定、相似三角形的性質;全等三角形的判定（SSS、SAS、ASA、AAS）以及全等三角形的性質;銳角三角形函數特殊值等數學相關知識，在知識復習系統復習中，讓學生以及題意和各個知識點進行問題生成，然后逐步演繹進行問題講解。

二、問題生成——優化思維

結合問題生成進行問題解決探索，優化思維能力，教師要著重于多角度進行思考，讓學生在一道例題中進行多元方法探索，運用多知識點進行問題解析。這樣既可以突破思維定勢，又可以培養數學思想，實現復習課教學質量的提升。如：

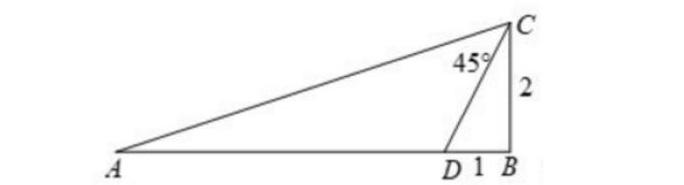
在Rt△ABC中，∠B=90°，BC=2，點D是AB上的一點，鏈接CD，已知BD=1，∠ACD=45°

對于這一問題，假使學生生成問題為：求AC邊的長。針對問題解決，教師可以聯合學生所提及的數學各個知識點入手進行解決思路優化，在一題多解中，優化思維，提高學習興趣。

方法一：按照題意進行條件提取，如∠ACD=45°，這一條件可知，需要放到直角三角形中。為此，針對AC邊長問題的解決來說，可以進行知識鏈接，結合直角三角形運用輔助線做相似，如過點D作DE⊥AC，如圖示：

在圖形搭建中，又題意可以得知：BC=2，BD=1，結合勾股定理，可以得知CD=BD2+BC2=5，∵∠ACD=45°，DE⊥AC，可知△CED為等腰直角三角形，CE=ED=102

設AE=x，則AD=x2+（102）2，由△AED∽△ACB可以得知：DEAE=BCAB=102x=21+x2+（102）2，求解X既可在這一解題方法的運用中，不僅考驗了學生對勾股定理的掌握，還檢驗了相似三角形，其中還設計到了相應的計算。但是從中考視野進行分析，計算量大，步驟也比較復雜，不利于提高學生的解題效率。為此，可以結合斜直角添加輔助線為輔助，進行“一線三等角”的構建，運用全等和相似進行解題優化，如：

方法二：過點D作DE⊥AC，過點E作EF⊥AB，如圖：

由△DEF≌△CDB推理得出：EF=DB=1，DF=BC=2

再結合相似得知：EFAF=BCAB=1x=23+x，解出x，得知AB，BC，從而進行AC求解。

思路清晰，解題過程簡單，其計算量也大大減少了，既可以提高解題效率和解題質量，又可以提高學生的數學學習能力，通過多元解題思路對比分析，促使學生在各個知識點應用中，進行思維提升。或者也可以直接運用初三所學相似進行直接求解，如：

這樣解析既簡單，同時也可以有效節省解題時間。

圍繞一個問題“求解AC的長”為中心，進行解題思路優化，在多角度解析中，激活思維，培養學生的數學學習能力。是復習課開展的中心主旨所在，同時也是教師教學重任。為此，在數學教學中，結合“一題一課”進行復習學習，教師要培養學生多元、多維思考問題的學習習慣，以一個問題為中心，進行解題策略優化，提高學習質量。同時為培養學生數學探究精神，在解題思路優化中，教師還要進行問題拓展，在題型變化中發散思維。

三、拓展提升——問題轉變

原題為：在Rt△ABC中，∠B=90°，BC=2，點D是AB上的一點，鏈接CD，已知BD=1，∠ACD=45°，是以生成求解AC的長為問題進行的解析和探究，那么，基于這一問題，可以轉化為，判斷題進行思維提升，如：

在Rt△ABC中，∠B=90°，AB=AC，點D是AB的中點，鏈接CD，過點B做BG⊥CD分別交于CD、CA于點E、F，與過點A且垂直于AB的直線相交于點G，鏈接DF，給出以下結論，判斷分析：

在進行問題判斷分析的時候，為提高課堂復習的趣味性，教師可以選擇五個學生進行問題驗證，運用相似△AFG∽△BFC進行問題一解答;運用△ABG≌△BCD（ASA）、△AFG≌△AFD（SAS）展開問題二的解答;結合△AFG≌△AFD，∴FG=FD>FE得知問題三解答;結合△AFG≌△AFD可得AG=12AB=12BC、△AFG∽△BFC，確定點F為AC的三等分點進行問題四解答;利用S△ABF=13S△ABC，又∵S△BDF=12S△ABF，等進行問題五的驗證。通過問題轉變，在拓展中，對相似三角形的判定與性質;全等三角形的判定與性質;等腰直角三角形等各部分知識進行有機關聯，讓學生知道各結論之間并非彼此孤立，而是往往存在邏輯關聯關系。在拓展提升，問題轉化中促使學生得到數學探究能力的培養。同時，在這一過程中，面對中考復習，教師要注意引導學生進行數學學習反思，在做題練習中反思自己對各個知識點掌握程度，明確不足，及時鞏固。以此來提高學習質量。

四、結語

從中考的角度進行“一題一課”復習課開展，教師要注意從一道題出發，培養學生的問題探究能力、發現問題的能力，在問題觀察、探索中培養提問意識，然后借助一題多解，從多角度進行問題思考，構建知識體系，最后借助拓展提升進行題型轉化，培養學生舉一反三的學習能力。在一題一課訓練中，提高教學質量，發展學生數學素養。

[參考文獻]

[1]俞衛斌.追尋“動中折疊”的足跡——一次“一題一課”公開課的教學實錄及點評[J].中學數學雜志：初中版，2019：42.

[2]王盈.精彩變式高效課堂——初三"一題一課"復習課的實踐與思考[J].課程教育研究：新教師教學，2019，000（036）：148-149.

[3]吳鳳樓.初中數學復習課"一題一課"教學思路探微[J].成才之路，2019（29）.

（作者單位：廣東省湛江市湖光第一初級中學，廣東 湛江 524088）