例談用“問題串”教學策略來建構高效數學課堂

唐曉芳

[摘? 要] “問題串”教學策略就是將“問題”作為整個教學活動的起點和主旨，不僅關注到教師“導”的過程，更關注到學生“學”的過程. 文章通過用“問題串”教學策略來驅動設計學習內容，將問題的解決與學生的學習相融合，在師生共同探究問題的過程中，習得數學知識，獲得“學問”及情感體驗，發展邏輯思維，從而實現真正意義上的高效數學課堂.

[關鍵詞] 高中數學;問題串;教學策略;高效

維果茨基的理論中曾談到高效的數學教學就是針對學生的“最近發展區”設計科學合理的問題串，并以此為載體來組織教學過程，讓學生的生命體自然生長，促進潛能的自然形成，為學生的個性成長搭建舞臺，為高效數學課堂助力■[1]. 因此，在實際教學中，教師需從具體教學內容和學情出發，從學生生命的視角播種，設計高效、適度的“問題串”，使之成為促進學生能力提升的階梯，關注數學教學的價值和數學本質，讓學生在“建構式生態課堂”中，不斷生長知識、方法和思維，不斷增長經驗和技巧，從而提升課堂教學的效果.

設計現實性“問題串”

教師充分關注學生已有的生活經驗，準確把握教學起點，通過設計與生產生活、科技實際等相關的現實性問題情境，來激發探究者的好奇和疑問，從而引發認知沖突，又以“問題串”貫穿整個教學的始終，讓學生的思維始終處于積極活躍的狀態，凸顯其應用性和實踐性，同時提高教學實效性.

案例1 以“平均變化率”的問題設計為例

問題1：游樂山車可以在4 s內迅速將速度由0 km/h提到190 km/h，接著又用8 s秒的時間沖刺至139 m的高度，最后歷經20 s穿過100 m的平行滑道.

師：請大家思考，問題1中哪些量發生了變化？

生1：速度、時間和位移.

師：不錯，回答得很全面. 繼續思考，速度又是如何變化的呢？

生2：一開始4 s內迅速將速度由0 km/h提到190 km/h，有著較大的變化，而最后歷經20 s將速度又回到0 km/h，相較于之前變化較小.

師：描述得很準確，此問題也可以提煉為“運動過程中變量的變化情況”. 下面我們再來探究問題2.

問題2：表1為某市3月至4月某日最高氣溫記載.

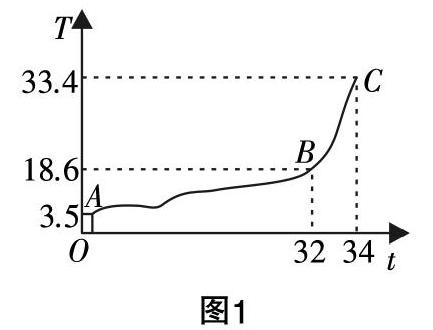
師：為了使問題2的研究過程更準確，如圖1所示，現呈現該城市3月18日至4月20日的氣溫變化曲線圖，在進一步的觀察中，你有何發現？（圖1中顯示：3月18日是第一天，4月20日是最后一天，共有天數34天，橫軸表示“天”，縱軸表示“溫度”.）

生3：據觀察可以得出，3月18日-4月18日的氣候變化較慢，4月18日-4月20日氣溫變化較快.

師：該如何形容這里的變化較快呢？是否可以通過分析圖像來體現？

生4：4月18日-至4月20日這兩天中氣溫陡然增加了14.8℃.

師：很準確的回答，不錯！因此，這時人們定會感嘆：“天氣忽然就熱了！”不過，經過觀察不難得出該市3月18日-4月18日氣溫由3.5℃到達18.6℃，二者溫差為15.1℃，略超14.8℃，針對這一情形，人們卻無多大感嘆，原因是什么呢？

（學生陷入思考）

師（點撥）：我們可以根據生4的回答思考如何刻畫這里的變量——氣溫的變化快與慢.

生5：圖中陡峭的程度是對氣溫變化的如實刻畫.

師：如何將這里的陡峭程度進行量化呢？

（大家又一次進入深度思考）

生6：可以用直線的斜率.

師：不錯. 我們可以比值■=■來近似量化此處點B、點C這一段曲線的陡峭程度，此比值為氣溫在區間[32，34]上的平均變化率，而再次計算得出氣溫在區間[1，32]上的平均變化率，從而可以得出溫差相同，而平均變化率則差距較大. 從中我們還可以感受到“以直代曲”的思想.

設計針對性“問題串”

筆者認為，在實施教學的過程中，首先需喚起學生的已有認知，再讓學生去分析、理解和驗證，從而有效梳理思維過程，建構知識經驗，最終達到熟練應用的目的. 因此，教師需從學生的已有知識經驗和能力基礎出發，有針對地設計與學生學習內容相貼合的“問題串”，有利于知識的理解和掌握，從而促進新知識的同化. 針對性的“問題串”是激發學生思維動機的重要渠道.

案例2? 以“三角函數的概念”的問題設計為例

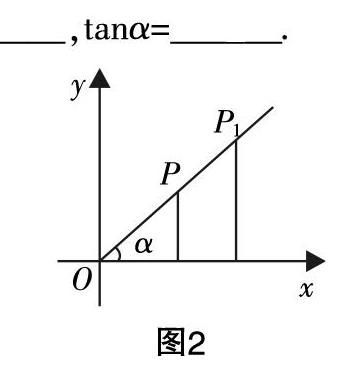
問題1：如圖2，點P在銳角α的終邊上，設點P（x，y），OP=r，則sinα=______，cosα=______，tanα=______.

問題2：如圖2，點P1在銳角α的終邊上，設點P■（x■，y■），OP■=r■，則sinα=______，cosα=______，tanα=______.

問題1與問題2的比值大小有何關系？

問題3：現擴大角α的取值范圍，當角α的終邊分別位于第二、三、四象限時，該如何定義任意角α，sinα，cosα，tanα？

問題4？搖現以原點為圓心，單位長為半徑作圓與角α的終邊交于點P，以上定義中的比值是否有變化？

教學分析：以上案例中設計具有針對性的“問題串”，一是符合學生的認知基礎，較易引發數學思考和深入討論;二是通過與教學目標相溝通的問題串，可以實現有效教學[2].

設計探究性“問題串”

法國數學家托姆曾說：學習應當是一個自發的探究過程，若認為死記硬背可以學到知識，那一定是一個可悲的錯誤認識. 這里就是強調，學習的過程并不是記憶的過程，而是以智力參與、自主探究和獨立思考為主導的探究活動. 這就要求教師需設計探究性“問題串”，讓學生的思維在問題的不斷探究中碰撞火花.

案例3 以“圓的性質”的問題設計為例

問題：已知圓C：（x-1）2+（y-2）2=1，C為圓心，點P坐標為（2，1），過點P作圓C的切線，切點為點A，B.

（1）試求出直線PA，PB的方程;

（2）直線l過點Q■，0，且被圓C所截弦長是■，試求出直線l的方程;

（3）試求出四邊形PACB的外接圓方程;

（4）試求出直線AB的方程;

（5）試求出弦AB的長;

（6）試求出■·■的值;

（7）試求出△PAB的面積.

探究1：已知圓C：（x-1）2+（y-2）2=1，C為圓心，點P在圓C外側，過點P作圓C的切線，切點為點A，B，試求出■·■的最小值.

探究2：已知動點P在直線3x+4y+8=0上，PA，PB為圓C：（x-1）2+（y-2）2=1的兩條切線，切點為點A，B，C為圓心，試求出△PAB面積的最小值.

探究3：已知圓M：（x-1）2+（y-2）2=1，M為圓心，點P坐標為■，■，相互垂直的兩條直線AC，BD過點P，且與圓M交于點A，C，B，D.

（1）圓心M到直線AC，BD的距離分別為d1，d2，試求出d1的取值范圍;

（2）求證：d■+d■為定值;

（3）試求出四邊形ABCD的最值.

教學分析：在以上問題的安排下，學生思維一直處于活躍狀態，在充足的自主探究時間內，對問題有充分的分析和認識，同時充分感悟到數學的創造美.

設計遞進性“問題串”

由于學生知識基礎和學習能力上的客觀差異，教師在教學過程中需關注學生的差異性，一改往日單一化的問題模式，采用低起點、小梯度、分層次的方法，設計出具有梯度的“問題串”，彰顯層次性和關聯性，讓每一個問題都成為思維的臺階，讓學生都可以參與到問題的探究中來，從而促進不同層次學生的共同進步.

案例4 以“向量數量積運算”的問題設計為例

問題1：已知向量a=（2，3），b=（4，1），試求a·b.

問題2：已知a=1，b=2，且a與b的夾角為120°，試求a·b.

問題3：已知a=1，b=2，且a與b的夾角為120°，試求出3a+4b的值.

問題4：已知a=1，b=2，且a與b的夾角為120°，試求出向量ka+3b垂直于ka-2b時k的值.

問題5：已知Rt△ABC中，有向量■=（3，2），向量■=（k，1），試求出實數k的值.

教學分析：此案例中，問題1和問題2是對基本知識的考量，由對向量數量積運算等基礎知識作鋪墊，實現由淺入深的知識鞏固;而問題3則是對向量模一般求法的考查;問題4和問題5實現了原有基礎的延伸和拓展，尤其是問題5還涉及分類討論的思想方法，幫助學生理清了數學知識的內涵與外延，在一次次梯度問題的成功體驗下，不僅提升了學生的學習興趣，還強化了學生的思維深度和廣度[3].

總而言之，數學教學的一項重要使命就是啟發學生的思考，我們只需在教學的每個環節設計好合理、科學的“問題串”，就一定可以為學生營造出個性化的生態課堂，使他們都可以得到應有的發展與進步，從而打造高效數學課堂.

參考文獻：

[1]? 張奠宙，張蔭南. 新概念：用問題驅動的數學教學[J]. 高等數學研究，2004（05）.

[2]? 季明. 試論高中數學高效課堂創設的途徑[J]. 理科考試研究，2014，21（11）.

[3]? 管明貴. 精心設計問題串，提高課堂教學效益[J]. 數學大世界（中旬），2017（04）.