小學數學教學中學生數學建模過程探析

顧瑋楠

摘? 要：數學教師研究學生的數學建模過程，才真正地抓住了數學建模教學的關鍵。從模型建構的角度來看：將學生思維加工的素材變成大腦中清晰的表象，然后尋找到判斷位置與方向的方法，才能夠幫學生建立起模型認識。數學建模的認知過程是：首先是知覺啟動，然后是圖式激活，再然后是數學表征，最后是模型運用。教師只有從學生學習的角度去研究數學建模的過程，才能真正掌握數學建模的規律，發現學生在數學建模過程中可能會遇到哪些挑戰，而有針對性地解決這些問題，也才能讓教師的數學建模教學水平日益提升。

關鍵詞：小學數學;數學建模;建模過程

數學建模在數學教學中的地位一直都是重要的，30多年前，義務教育各個學科曾經出版過一套關于建模的書籍，而事實上，關于數學建模的研究，在那之前早就開始了。直到今天數學學科核心素養的提出，數學建模依然在其中占有一席之地，而在數學教師的教學研究情境中，數學建模更是作為一個掛在口頭上的概念而頻頻被提及。

什么是數學建模？數學建模就是運用數學的思想、方法和知識建立數學模型的過程。這是一個非常學術的表達，甚至因為過于學術化，而顯得有些不接地氣。相信多數一線教師是不喜歡這樣的表達的，如果思考得更加深刻一些，還會發現其中存在著另外一個問題：如果說教師對數學建模的理解因為概念化、學術化而有些模糊的話，那么又如何真正認識到學生的建模過程是怎樣的呢？要知道，作為一個數學教師，如果不知道學生的數學建模過程是怎樣的，那么數學建模的教學就難免以己昏昏而使生昭昭了。因此筆者認為，數學教師研究學生的數學建模過程，才真正地抓住了數學建模教學的關鍵，小學數學教學中關于數學建模的研究成果，可以說是車載斗量，而將目光鎖定在學生建模過程的研究并不多見，筆者不揣淺陋，決定做一個嘗試。

一、小學數學建模理解：從宏觀到微觀

首先可以肯定的是，數學建模對于小學生的數學學習而言，意義是不言而喻的。將數學建模思想應用于小學數學教學過程，能較好地簡化抽象數學知識的難度，有利于構建學生數學知識網絡，樹立學生信心，提升學生課堂參與度，從而提高教學效率。可以說這是一個比較公認的判斷，但筆者仍然想強調，對小學數學建模的理解，仍然應該更細致一些，應當堅持從宏觀到微觀，只有體察入微，才能知道學生在數學建模過程中會經歷了一些思考，會遇到哪些困難，教師的數學建模教學才能真正做到有的放矢。也就是說，教師在教學中引導學生建立數學模型，不僅要重視其結果，更要關注學生自主建立數學模型的過程，從而讓學生在進行探究性學習的過程中科學地、合理地、有效地建立數學模型。

例如，在“位置與方向”的教學中，幫學生認識位置與方向，看起來是一個常識教學，實際上卻是為了幫學生建立模型。有經驗的小學教師都知道，相當一部分學生對位置與方向的判斷是模糊的，不少學生甚至到小學畢業都難以迅速地判斷東西南北，在讓人啼笑皆非的同時，卻又應當引發思考：位置與方向的教學，如何才能在數學建模的思路之下，更好地達成預期的效果。

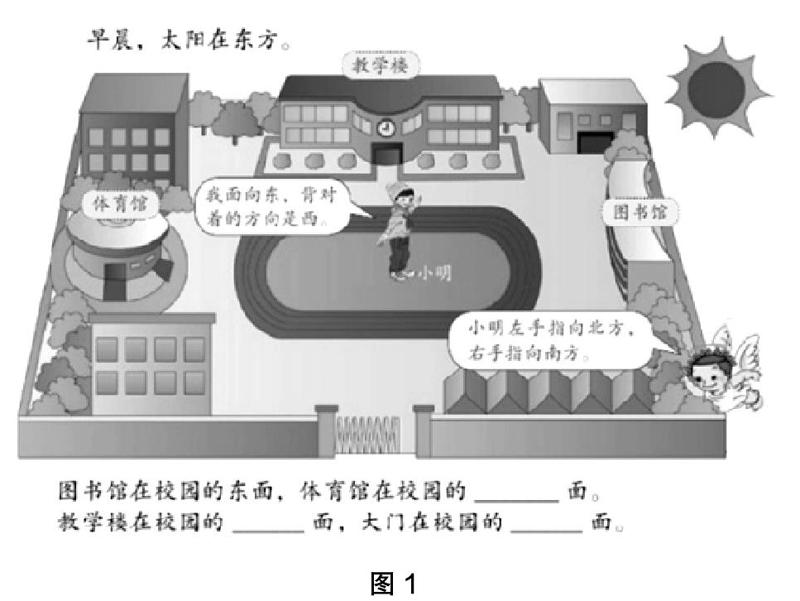
筆者的觀點仍然是，要從微觀的視角研究學生的數學建模過程。在“位置與方向”的教學中，教材給學生設計了一個具體的情境（如圖1），然后讓學生根據太陽的位置以及相關的說明，去判斷一些建筑物的位置;實際教學中，可以將這一畫面轉換為學生的具體學習生活環境素材，如直接向學生提問：我們上課的教室在學校的哪個位置？學校大門在哪個方向？……

但是這樣是否就能夠幫學生建立起位置與方向的認識呢？筆者以為是值得商榷的。筆者研究過：對于這些問題的回答，回答正確的學生憑借的是經驗，回答錯誤的學生缺少的是表象（也可以說是模型認識），因此只是這樣的一問一答，是不足以培養學生的模型認識的。從模型建構的角度來看：將學生思維加工的素材變成大腦中清晰的表象，然后尋找到判斷位置與方向的方法，才能夠幫學生建立起模型認識。

二、小學數學建模過程：從現象到本質

基于以上分析，教師將研究的視角從宏觀轉向微觀，那對數學建模的過程就要從現象轉向本質。談到本質，數學教師一般都知道，數學在本質上就是在不斷的抽象、概括、模式化的過程中發展和豐富起來的。數學學習只有深入到“模型”“建模”的意義上，才是一種真正的數學學習。而從認知的角度去理解并設計數學建模的過程，顯得非常必要。

同樣以“位置與方向”的教學為例，基于數學建模的教學設計一般是這樣的：

首先，創設情境，讓學生判斷位置與方向。這一步以上述第一點中的素材為情境素材，具體不贅述。

其次，數學體驗，幫學生建立“位置與方向”表象。這一步主要是在學生已有經驗的基礎上，讓學生通過畫圖的方法，去將自己對位置與方向的認識用圖表示出來。這里涉及一些細節，比如畫圖時對“上北下南、左西右東”方向的確定，又比如將實際的位置轉換為圖上的位置，等等。畫圖實際上是一個輸出的過程，也是讓表象變得更加清晰的過程。

再次，數學應用，幫學生強化模型認識。這一步強調的是遷移，也就是讓學生將自己對位置與方向的認識，運用到新的生活情境當中，比如讓學生拓寬視野，畫出上學一路標志性建筑的位置，等等。

如果說教學設計是現象角度，那么認知的角度就是本質。數學建模的認知解釋是這樣的：首先是知覺啟動，然后是圖式激活，再然后是數學表征，最后是模型運用。從這個視角去看上述教學設計：利用生活經驗創設情境實際上就是為了啟動學生的知覺;而建立表象實際上就是激活學生的圖式，如果學生的圖示不夠完整，那么教師就要在教學中采用多種方式，如講授或者學生之間的合作等;當圖示完整之后，就要進行輸出，這也就是數學表征，畫圖就是一種很好的表征方法，尤其適合小學生的數學建模，即使不是“位置與方向”這樣的知識，很多時候也可以選擇畫圖的方法;而最后數學應用的過程，首先是為了幫學生檢驗所建立起來的模型是否合理，實際上不少學生對上北下南、左西右東的規則比較抗拒，他們也確定了自己的表示方法，但是在交流的時候就出現了困難，于是對方向的約定俗成，就使得他們改變了原來的思路。

事實上，通過上述教學設計，小學生對位置與方向的確定就進入了同一個模式，自然運用的也就是同一種模型，這個過程如果得到適當程度的重復，學生對這個模型的理解與運用就會變得越來越熟練。

三、小學數學建模評價：從經驗到解析

作為教學研究的一部分，對數學建模的評價，影響著教師對數學建模的認識。同樣從學術語言的角度來看，數學建模的本質，在于它更突出地表現了原始問題的分析、假設、抽象的數學加工過程，數學工具、方法和模型的選擇分析過程，模型的求解、驗證、再分析、修改假設、再求解的過程，體現了學數學和用數學的關系。如果將這一學術判斷轉化為經驗判斷，可能更加符合小學一線教師的需要，只不過這種經驗判斷不應當是純粹經驗的，而應當是經驗解析式的。

上述第二點提供的認知視角，實際上就是一種很好的解析工具，甚至可以認為認知視角下的數學建模評價，本身就是一種模型：知覺啟動——圖式激活——數學表征——模型運用，就是認知視角下數學建模模型的初步表述。在這個模型當中，每一個環節以及每一次轉換都有著豐富的研究空間：小學生的知覺如何啟動？知覺啟動是否必然激活學生的圖式？用怎樣的數學語言去表征形成的圖式？如果建立起來的模型不符合預期，那該怎么辦？對這些問題的思考與回答，實際上就可以驅動教師去研究學生的數學建模過程，同時也就決定了數學建模教學的質量。

筆者在教學實踐中，對數學建模評價的解析視角，實際上進行過多次比較，結果發現從認知視角去進行解析，要比從經驗角度去解析可靠的多。當然，上述認知視角還顯得比較籠統，其中的每一個環節與環節轉換，還存在著豐富的研究細節，比如在圖示激活環節，學生可能會在自己的知識與經驗系統中進行多次搜索，這里有一個匹配與識別的過程，也非常值得研究。總的來說，教師只有從學生學習的角度去研究數學建模的過程，才能真正掌握數學建模的規律，發現學生在數學建模過程中可能會遇到哪些挑戰，而有針對性地解決這些問題，也才能讓教師的數學建模教學水平日益提升。