優選初中數學新課導入模式，提升教學有效性

陳媚娜

[摘? 要] 新課導入的方式多種多樣，但終其目的就是要引導學生樂于學習，善于學習，文章根據初中學生的年齡特點，知識水平的實際情況，從多個角度、多個方法探討了各種課堂導入的途徑，為初中數學教學提供了很好的教學參考.

[關鍵詞] 初中數學;新課導入;數學教學

新課導入，就是通過一定的方法引出所要講述的章節內容，把學生領進學習的“大門”. 教師采用不同的導入法生動地導入新課，就像廚師每天變換花樣做出各種佳肴，學生自然會被激發出極大興趣，能集中精力投入到新課的學習中去，從而產生事半功倍的教學效果. 對于不同的課題內容，針對性地使用不同的途徑，將學生引入新的情境，使其在興趣中學習，在好奇中學習，在主動中學習，這是教師備課的基本環節. 教師在教育教學中不能因為新課引入只是教學中的一個小環節而忽視了這個模塊的設計. 可以說，一個好的新課導入設計能緊扣學生的思維，引導學生主動參與數學課的活動并全身心地投入到課堂的教與學上，這些都是提高教學有效性的前提. 筆者根據多年的初中數學教學經驗，總結以下幾種數學新課導入的途徑.

設疑法——創設懸念，扣人心弦

借鑒說書人“且聽下回分解”的妙術于數學課堂教學導入時的情境創設之中，以懸念作為挑逗學生好奇心的觸發點，使學生產生一種強烈欲望，而一旦引起這種欲望，學生就非要扒根究底，弄個水落石出不可[1] . 激發學生的好奇心和求知欲，能使學生產生濃厚的學習興趣，從而渴望學數學，做數學.

案例1? 在教授“平方差公式”這一節課時，設置問題：李明同學去商店買了單價是9.8元/千克的糖果10.2千克，售貨員剛拿起計算器，李明就說出應付99.96元，結果與售貨員計算出的結果相吻合. 售貨員很驚訝地說：“你好像是個神童，怎么算得這么快？”李明卻說：“這沒什么，我只是運用了剛剛學到的數學公式而已. ”教師提問：“同學們，你們知道李明同學用的是一個什么樣的公式，怎么得到答案的嗎？”這時班級有5名學生舉手想回答這個問題. 此時教師便自然地引入：這個奧妙就在于接下來要講解的“平方差公式”. 這節課讓教師意外的是全班都非常認真，教學過程非常順利，當然也得到了很好的教學效果. 下課前教師引導學生回顧：“開頭的情境問題，你能解釋嗎？”全班同學都舉手示意，最后教師選了一名學困生上臺講解，獲得了陣陣掌聲. 通過對課堂的觀察與反思，這個新課引入的方式起到了重要的作用，激發了學生的求知欲，引導學生參與課堂，進入自主學習模式.

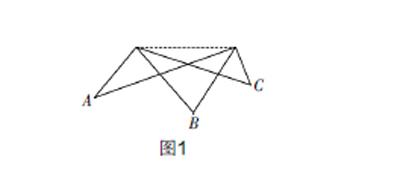
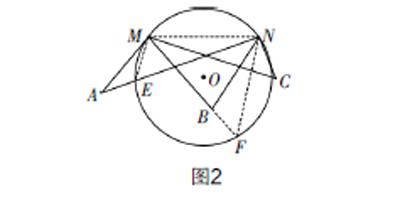
案例2? 在教授“圓周角”這一節課時，設置情境問題：如圖1所示，讓運動員們分別在A，B，C點所處的位置上，哪個點位射門最容易得分？哪個點得分的難度大？為什么？這個問題可以用今天這節課要學習的“圓周角”來解釋. 這節課同學們興趣盎然，甚至有一個男生催促著老師趕緊教授新知識，迫不及待想學成后向足球迷爸爸“賣弄”這個問題，當然這節課也得到了很好的教學效果. 學完圓周角性質“同弧或等弧所對的圓周角相等”后教師引導學生回顧：“開頭的情境問題，你能解釋嗎？”教師借助圖2分析原理，謎底揭開后，同學們豁然開朗，似乎還有一種“知其然更知其所以然”后的意猶未盡.

玩游戲法——創設游戲情境，寓學于樂

“玩游戲”對于學業壓力已經慢慢變重的初中生來說似乎是幼兒時期的記憶，如果一向以嚴肅著稱的數學老師可以帶著他們做點游戲，學生一定對這個數學老師充滿了好奇，也會消除對數學課的焦慮. 基于初中生天性愛玩好動的特點，只需合理地設置游戲環節，寓學于樂，便可以良好地調動學生的多種感官，極大地提升學生的學習興趣. 通過創設游戲情境導入新課，可以使學生在游戲中動手、動腦、動口、開心地合作，把抽象的數學知識趣味化，讓枯燥的教學活動生意盎然.

案例3? 在講授華師大版15.3“中心對稱”這一節課時，筆者設置了這樣一個游戲：首先使用事先備好的“非中心對稱”的數張撲克牌進行展示，將其按照牌面的數字大小理好順序，讓一位同學從老師手中任意抽出一張，記住這張撲克的數字和花色，在讓這位同學把這張撲克牌按原方向插回前，老師要悄悄地把手里的撲克牌旋轉180度，緊接著再請這位同學洗牌，然后展開撲克牌，老師可以很神奇又準確地找到同學原先抽出的是哪一張撲克牌，即便游戲推倒重來，老師的結果還是正確的. 這堂課上學生都爭著要參與到這個游戲中，當教師在解釋其中奧秘的時候，學生都表現出了求知若渴的樣子. 顯然，課堂效果也已經達到了預期. 在“撲克牌游戲”的過程中，學生已經在玩樂的同時鍛煉了觀察、發現、總結、歸納的能力，強化了對中心對稱圖形的理解，加深了對其特點的印象，從而發展更直觀的空間觀念，也更好地感受到了數學的趣味性、探索性. 這樣的新課導入法一方面使學生體會了成功的喜悅，另一方面又能培養學生的概括及觀察能力，可謂一舉兩得.

講故事法——創設故事情境，興趣盎然

好的故事不僅具有強大的吸引力，還能感染人的情感，激發內在的情愫. 針對學生愛聽他們似懂非懂的故事的心理特點，教師精選一些與教學內容有關的故事來導入新課，不僅可以活躍課堂氣氛，還能拓寬學生視野，讓學生的思維在新的故事情境中活躍起來，使學生輕松掌握其中蘊含的數學知識.

案例4? 在教授“無理數”這節課時，用無理數的發現這一故事來引入新課：古希臘有位杰出的數學家名為畢達哥拉斯. 他開了一所名叫“畢達哥拉斯學園”的學校，大家都很敬重地稱呼他們為“畢達哥拉斯學派”.[2]在他的眼中，數是主宰生死的力量，是世界上最重要的法則，應當把數像天神一樣崇拜. 地球上只能有整數與分數，絕對不可能存在其他的數. 直到有一天，他的一位名叫希伯斯的學生，在計算邊長為1的正方形對角線的長度時，發現結果非常的奇特，答案既不是整數，也不是分數. 這無疑會嚴重打擊畢達哥拉斯的理論以及他在學術界的地位，因此畢達哥拉斯嚴厲訓斥并警告他不得將這個發現向世界公布，否則要把他活埋. 但真相怎么能被掩蓋呢，希伯斯和他人私下偷偷地討論這個驚人的發現，這個發現很快就被傳開了，為防生命危險，他被迫外逃. 希伯斯在國外流浪了好幾年，后來由于思念家鄉，他偷偷地返回希臘，在地中海的一條船上被“畢達哥拉斯學派”的弟子發現后殘忍地扔進了大海. 后來人們把希伯斯發現的新數起名叫“無理數”，一方面紀念希伯斯為科學的獻身精神，另一方面諷刺“畢達哥拉斯學派”的不講道理. 顯然學生的思緒被帶進了故事中，他們感受到了數學史發展的曲折過程，培養了他們對科學知識的敬畏態度，懂得珍惜當前的學習. 在講述這個故事時，學生流露出的表情有震驚、感慨、憤怒、敬佩等，該引入法事半功倍的作用很明顯.

實驗法——創設操作情境，動手實踐

《數學課程標準》指出：“有效的數學學習活動不能單純地依賴模仿與記憶，動手實踐、自主探索與合作交流是學生學習數學的重要方式. ”[3] 教師應當設法來創設操作情境，引導學生進行細致的觀察并學會分析，主動尋找其中的規律，讓思維從感性層面逐步過渡到理性層面，使抽象概念形象化、生動化. 實驗引入法就是通過讓學生動手操作，從而引入新知識的過程，由此提高其觀察能力、思維能力. 該引入法的突出優勢在于富有啟發性和趣味性，可以更加形象生動地對抽象問題進行闡述，知識的引入顯得很自然，同時也讓抽象的問題通俗化.

案例5? 在進行“三角形內角和定理”這一課的引入時，教師請所有的學生都在紙上隨意繪制一個三角形，將三角形的每個角剪下來，再將三個內角拼湊成一塊，接著就可以引導學生進入思考環節：這三個內角的和等于多少度？由此引入三角形內角和定理. 教師在組織學生進行這個實驗時，學生遇到新的問題后會有急于求成的心理需求，在這樣的背景下，教師進入自己的教學活動，帶領學生一起探索問題的答案，學生是非常愿意配合的.

歸納法——歸納情境問題，培

養歸納能力

歸納猜想是揭示科學規律的重要方法，歸納導入法是通過對一類數學對象進行不完全歸納來導入新課的一種方法，也是數學導入新課常用的方法.

案例6? 在教授“有理數的乘法”這一節時，多媒體顯示：一個玩具汽車沿直線L前進，點O為直線L上的一個點. 當前汽車位于點O. （方向：向左為負，向右為正;時間：現在前為負，現在后為正）

（1）假設玩具車按照每分鐘2米的速度向右前進，3分鐘后它在什么位置？

（2）假設玩具車按照每分鐘2米的速度向左前進，3分鐘后它在什么位置？

（3）假設玩具車按照每分鐘2米的速度向右前進，3分鐘前它在什么位置？

（4）假設玩具車按照每分鐘2米的速度向左前進，3分鐘前它在什么位置？

分析：

（1）3分鐘后玩具車應在O點右邊6米處，算式為：（+2）×（+3）=+6;

（2）3分鐘后玩具車應在O點左邊6米處，算式為：（-2）×（+3）= -6;

（3）3分鐘前玩具車應在O點左邊6米處，算式為：（+2）×（-3）=-6;

（4）3分鐘前玩具車應在O點右邊6米處，算式為：（-2）×（-3）= +6.

接著教師以問題為中心，引導學生思考：這些算式里，積的絕對值與兩個因數的絕對值有著何種聯系？積的符號和兩個因數的符號又存在何種聯系？ 讓學生自己小結歸納法則. 顯然學生在歸納中還可以借助類比遷移，將知識點有機地串聯起來，有助于學生弄懂知識結構，構建知識體系，進一步提高教學效果. 可以說歸納總結的能力在課上就得到了加強，突破了之前的學習模式.

復習引入法——復習現有的知

識背景達到溫故而知新

通過復習已學過的知識，引入新課的學習內容，這種引入的特點是便于促使學生實現知識和思維的正遷移，更好地從系統上串起知識結構. 該引課法更適合于判定和性質的運用這類新課.

案例7? 在講授“平行四邊形的判定”時運用復習引入法，把之前學過的“平行四邊形的性質”重新復習一下. 這時教師可以提問：“剛才我們復習了平行四邊形的邊、角、對角線的特殊性質，那么四邊形的邊或角或對角線滿足什么特征就可以成為平行四邊形呢？今天，我們就來學習平行四邊形的判定. ”這樣就很自然地引出本節課所要學習的內容. 這種方法有利于學生在學習過程中去比較性質與判定的不同，還能讓學生在學習的過程中不感到生疏，利于新課的展開.

直接引入法——直接揭示課題，

一目了然

直接引入法也可稱為“開門見山”引入法，不用拐彎抹角，而是干凈利落地點明本節課的學習重點、難點以及學習要求，以期學生在最短的時間內明確本節課的學習任務，簡單容易，好處在于可以節約大量課堂時間. 如果新舊知識無明顯聯系，那么使用該引入方法直接切入主題就最為適宜. 但學生面對的是全新的課題，陌生的內容對學生的注意力提出了更高的要求，思維必須緊跟教師的講解，對于基礎較為薄弱的同學，其學習的節奏不容易跟上. 由于很多教師常年使用這種方法，大部分學生還是會習慣性地覺得目標明確. 例如講授“圓的認識”就可采用直接引入法. 不過，由于不少教師經常用該方法來引入，而且常常連續使用同一種方法，這樣容易導致學生感到乏味，難以引發學生的學習積極性，這也是使用直接引入法應當注意的地方.

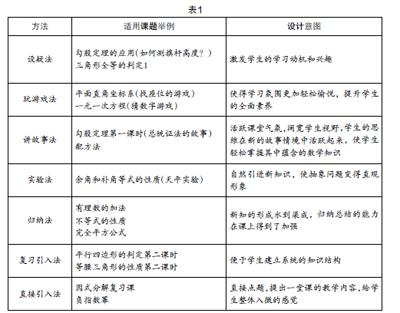
表1是筆者列舉的一些關于新課導入的例子，可供參考.

綜上，雖然優秀的教學方法有無數種，但遴選出最適用的優化教學的方法應當是教師要掌握的一項重要技能. 對教學方法進行優化選擇，在備教學目標，備教學內容，備學生學情的基礎上，教師還應該備好教學方法. 設計一節好的新課導入目的是使學生產生一種主動積極的態度，充分發揮自身非智力因素，從而實現《新課程標準》提出的“人人學有價值的數學，人人都能獲得必要的數學，不同人在數學上得到不同的發展”. 新課導入的類型和方法是很多的，但不管是何種方法都是為教學服務的. 在整個數學教學活動中教師應想方設法設計好每節課的導入環節，導入必須服務于既定的教學目標，必須服從于教學內容，必須符合學生的實際，必須簡潔而緊湊. 教師在教育教學中應該要善于反思，根據學生已有知識、年齡特征及心理特征來設計新課的導入，不能忽視，更不能流于形式.

參考文獻：

[1]章楠. 基于探究式教學的初中數學課堂導入研究[J]. 數學教學通訊，2019（11）.

[2]植華燕. 高中數學課堂引入藝術[J]. 中學數學研究（華南師范大學版），2014（21）.

[3]黃榮. 基于數學課程標準的教學設計與思考——以“極大值與極小值”為例[J]. 數學通訊，2018（12）.