從圖形直觀到算式抽象

李小強

作為《義務教育數(shù)學課程標準（2011年版）》十大核心概念之一，幾何直觀是幫助學生描述和分析問題的重要工具。在幾何直觀中，圖形直觀又是一個重要分支，在教學中有著廣泛的應用，其中，線段圖就是最抽象的圖形直觀，也是最簡潔的圖形直觀。對于三年級學生來講，他們已經具備了讀懂數(shù)線圖（再抽象一下就是線段圖了）的基本經驗，能夠通過數(shù)線圖列出算式。然而，在解決實際問題時，學生卻很難將畫圖的方式用于分析問題的過程中，筆者曾對某班三年級學生進行了畫圖分析問題的調查，有84.3%的學生不明白怎樣畫圖，或不明白如何在圖中標注信息。徐斌老師的“畫線段圖解決問題”更加側重圖形直觀到算式抽象之間的過渡與銜接，從“線段圖怎么來的”和“怎么畫出線段圖”兩個角度幫助學生更深入地認識和理解線段圖，讓學生知其然更知其所以然。

【片段一】三問“變與不變”，抽象得到線段圖

師：徐老師要考驗大家的眼力。如圖1，你能發(fā)現(xiàn)數(shù)學信息嗎？

生：有2朵藍花（圖中用白色表示，下同）。

師：如圖2，現(xiàn)在誰能用數(shù)學語言描述一下？

生：紅花（圖中用黑色表示，下同）是藍花的4倍。

師：對，紅花的數(shù)量是藍花的4倍。如圖3，繼續(xù)觀察，現(xiàn)在什么變了，什么沒有變？

生：圖形變了，但數(shù)量沒有變，顏色也沒有變。

師：那這個時候紅色正方形的數(shù)量是藍色正方形的幾倍？

生（齊）：4倍。

師：如圖4，現(xiàn)在呢？什么變了，什么沒有變？

生：現(xiàn)在有4個紅色長方形，有1個藍色長方形，紅色長方形的數(shù)量是藍色長方形的4倍。

師：你說得真完整。

師：如圖5，這樣呢？紅帶子的長是藍帶子的幾倍？

生（齊）：4倍。

師：認真觀察圖6，什么變了，什么又沒有變？

生：除了帶子寬度變了，其他都沒有變。

師：也就是說，原來很寬的帶子，現(xiàn)在只是變窄了，長度和顏色都沒有發(fā)生變化。這個時候，紅帶子的長是藍帶子的幾倍呢？

生（齊）：4倍。

師：仔細看圖7，它變得更細了。你見過這樣的圖形嗎？它叫什么呀？

生（齊）：線段圖。

師：現(xiàn)在，你知道線段圖是怎么來的了吧？其實，我們平時生活當中的一些現(xiàn)象或圖形，最后都可以變成像這樣的線段。今天，我們就來學習畫線段圖來解決問題。

【賞析】在以往的數(shù)學教學過程中，我們往往只重視線段圖的工具性，用它分析和解決問題，卻極少去思考線段圖是怎么來的。所以，學生對于線段圖的認識是片面的。本節(jié)課，徐老師通過3次圖形的變化，讓學生對線段圖有了更深刻的認識和理解。其中，第一次變化是基本的數(shù)學抽象過程，從具體實物（花朵）到數(shù)學圖形（正方形），即從生活到數(shù)學的過程，讓學生明白線段圖可以解決生活中的問題，而且解決的是一類問題，而不是一個簡單的“紅花的數(shù)量是藍花的4倍”的問題。第二、三次圖形變化分別是從獨立的多個正方形拼接成完整的一條帶子，再從寬寬的帶子壓縮為細細的線段圖，讓學生在“變與不變”之中深刻理解數(shù)量關系，抓住數(shù)學本質，同時又體會到畫圖的簡潔。

【片段二】三改“問號位置”，深刻理解線段圖

師：在生活當中遇到的實際問題，有的沒有告訴我們要求什么，有的還需要我們去尋找已知信息。你們能夠自己發(fā)現(xiàn)問題和提出問題嗎？來看這樣一個情境（情境圖略，圖中的數(shù)學信息：褲子48元，上衣的價錢是褲子的3倍），你能發(fā)現(xiàn)哪些已知的數(shù)學信息？

生：褲子的價錢是48元。

生：上衣的價錢是褲子的3倍。

師：這些都是題目告訴我們的，叫作已知條件。根據(jù)這兩個條件，誰能提出一個數(shù)學問題來？

生：上衣要多少元？

師：一件上衣多少元？（記作1號問題）誰能提出不一樣的問題？

生：一件上衣和一條褲子一共多少元？

師：一件上衣和一條褲子就可以簡稱一套，那就是一套衣服多少元？（記作2號問題）誰還能提出一個不一樣的問題？

生：一件上衣比一條褲子貴多少元？（記作3號問題）

師：根據(jù)條件，我們提出了3個問題，接下來就要解決問題了。這3個問題都很好，不過難易程度不一樣，你認為哪個問題最簡單？

生（齊）：1號問題。

師：那我們就從1號問題開始吧。徐老師有個要求，今天，我們不是直接解決這個簡單問題，而要一起來畫線段圖。

（畫線段圖：第一，如圖8，教師示范畫線段圖，提示學生畫線段圖之前先計劃一下，并記得寫上褲子和上衣，然后，畫出了一條線段代表褲子，標上了數(shù)據(jù)。第二，如圖9，學生在作業(yè)紙上畫出上衣所對應的線段，一個學生代表在黑板上畫圖）

師：上衣的價格是褲子的3倍，就要畫這樣的幾段（教師用手比畫）？

生（齊）：3段。

師：很好，把已知條件都畫出來了。現(xiàn)在，我們需要在圖中標出問題。

（學生在作業(yè)紙上標注，一個學生代表在黑板上標注“？元”）

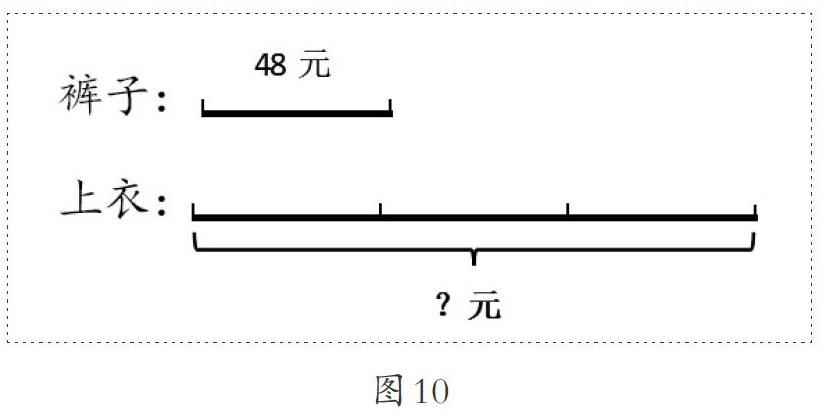
師：這就是線段圖。如圖10，請大家再看看屏幕上的圖和文字，再看看線段圖，你看到線段圖有什么樣的感覺？

生：剛開始看這道題時，理解還有些困難。但當畫出線段圖后，就可以理解這道題了。

師：請看圖10，這是褲子的價錢（48元）。這是上衣的價錢，相當于幾條褲子的價錢（3條）。誰能夠直接列算式求出上衣要多少錢？

生：3乘以48等于144元。

師：很好，1號問題解決了。我們來看2號問題，這個線段圖的問號還能表示一套衣服的錢數(shù)嗎？

生（齊）：不能。

師：既然不能，請你用橡皮把代表上衣價錢的這個問號擦去，再想一想，一套衣服的價錢應該在線段圖上怎么表示？

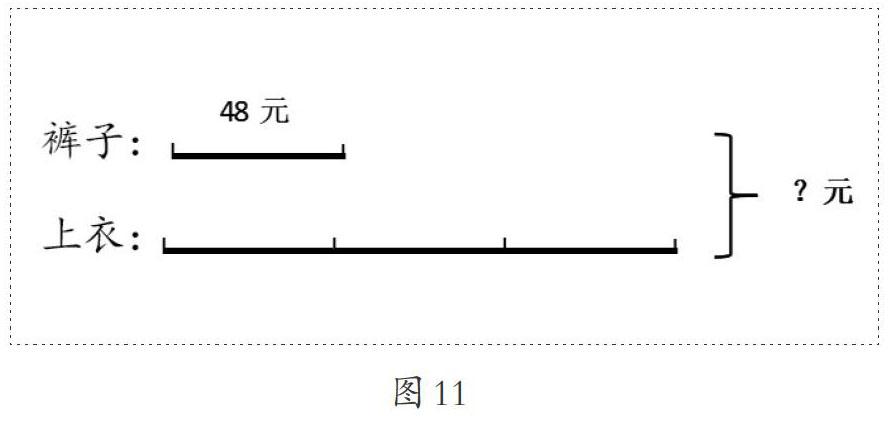
（一個學生代表在黑板上畫圖，如圖11。之后，教師要求其他學生根據(jù)黑板上的做法，修改自己的線段圖）

師：線段沒有變化，現(xiàn)在要表示一套衣服多少元，他在這里標上了問號，對嗎？（學生點頭示意）請你列算式計算，想想先算什么，再算什么？

（學生在作業(yè)紙上自主解答問題，教師選擇兩個學生代表板書自己的算式）

師：兩個同學的結果都是192元，但是算式有點不一樣。誰能明白這里的48×3求出的是什么？（教師指著第一種算法）

生：求出的是上衣的價錢。

師：對，就是上衣的價錢，再加上褲子的價錢，就是一套衣服的價錢了。我看到大部分同學是這樣算的。再來看看第二種算法，老師有些看不懂了，哪個同學能幫老師解釋一下小括號里面的“3+1”是什么意思？

生：上衣有3份，褲子有1份，一套就有4份，每份都是48元，所以用48×（3+1）計算，一共192元。

師：同學們真厲害，不僅會畫線段圖，而且解決一套衣服要多少錢這個問題時還用了兩種不一樣的方法。

師：現(xiàn)在我們一起來解決3號問題。首先要自己讀題，再用橡皮擦掉表示“一套衣服多少錢”的那個問號，思考怎樣表示上衣比褲子貴的錢數(shù)，最后在作業(yè)紙的空白處列出算式。

（學生在作業(yè)紙上自主解答問題，教師請一個學生代表畫出表示上衣比褲子貴多少錢的問號，如圖12。之后，學生自由表達自己的想法，教師板書算式）

師：誰來說一下自己列出的算式，并解釋一下。

生：3×48-48。3乘48表示上衣的價錢，再減去褲子的價錢48元，就求出上衣比褲子貴了多少錢。

師：和他一樣做法的同學請舉手。有沒有誰的方法和他的不一樣，也能求出來呢？

生：我列的是48×（3-1）。一件上衣是一條褲子的3倍，用上衣的3倍減去褲子的1倍就是2倍了，再乘以48就是上衣比褲子貴的錢數(shù)了。

師：你的思路基本準確，和他的做法一樣的同學請舉手。

師：剛才，我們一口氣提出并解決了3個問題。回顧一下，今天解決問題和以往解決問題好像略有不同，我們是用什么樣的解題策略來解決問題的？

生（齊）：畫線段圖解決問題。

【賞析】發(fā)現(xiàn)問題、提出問題、分析問題和解決問題是學生應該具備的4項關鍵數(shù)學能力。首先，思考源于問題，徐老師引導學生在尋找數(shù)學信息的過程中發(fā)現(xiàn)情境中的已知條件，讓學生讀懂情境，又鼓勵學生從不同的角度提出了3個典型數(shù)學問題，這些問題均源于學生對題目的理解，有利于教師更好地讀懂學生。

其次，分析問題是解決問題的關鍵環(huán)節(jié)，徐老師引導學生利用畫線段圖分析問題，很好地抓住了題目中的“變與不變”，逐次突破教學重、難點。不變的是已知條件和信息，變化的是所提出的數(shù)學問題，如何解決這樣的矛盾呢？徐老師巧妙地借助確定問號的位置，為學生建立文字信息與圖形直觀之間的聯(lián)系，幫助學生深刻理解線段圖，為用好線段圖奠定基礎。

其中，線段圖發(fā)揮著重要的作用，比如，在解釋“用48×（3+1）求一套衣服多少錢”和“用48×（3-1）求一件上衣比一條褲子貴多少錢”時，線段圖的直觀與形象，幫助學生清晰地理解“3+1”和“3-1”所表示的意義，一目了然。假設沒有線段圖，學生很難解釋和理解它們表示的意義，更有甚者，可能學生不會想到用這兩種算式來解決問題。

在解決問題中，我們需要用圖形直觀來解決問題，也需要用算式抽象來解決問題，但更重要的是從圖形直觀到算式抽象的過渡。本節(jié)課，一是在變化的圖形中發(fā)現(xiàn)不變的數(shù)量關系，解釋線段圖的由來;二是在不變的線段圖信息中尋找變化的問號在哪里，幫助學生學會畫線段圖。這樣一來，抽象的算式也能形象地解釋，有利于學生解決問題。

（作者單位：陜西省西安市長安湖居筆記小學）