基于兒童視角，妙用 數學史教學的策略

李友

德國數學家克萊因提出：“歷史呈現了知識的來龍去脈，敘說了人類認識如何步步深入，在抽象的過程中我們就能體會和把握認識提升的關鍵。”將數學史巧妙地在小學課堂教學中再現，是幫助兒童主動提煉數學信息、探求數學新知、解決數學問題、展現數學思維的一個重要途徑。選擇符合兒童心理特征和認知規律的數學史進行教學，能激發兒童對數學學習的興趣，使課堂教學生動、高效，讓兒童快速、牢固地完成知識構建，也能讓兒童感受到數學的形成與發展的過程，體會到人類通過數學認識自然世界、改變世界的歷程。實踐證明，數學學習中滲透數學史，會激發學生的數學思考，數學學習將因此變得更有意義、更有內涵、更加豐厚。筆者從以下三個方面闡述在數學課堂中如何運用數學史進行教學。

一、引入歷史故事，構建新知網點

數學歷史故事精彩而生動，常常能扣人心弦，引發學生共鳴，使人久久回味。在教學中，教師追尋歷史長河中某些數學知識產生過程中遇到的人和事，基于兒童年齡特點和個性差異，以“兒童為本”組織教學，從兒童學習數學的認知結構的需求出發，精心選取數學史資料中與學生構建新知相近的故事，巧妙地將相關的數學歷史故事引入課堂教學，引領學生在故事中開啟思維，拓寬認知邊界，把握知識節點，促進數學理解，更好地幫助學生厘清一個個知識產生和發展的脈絡，有序編織堅固的知識網。

例如，在教學人教版數學三年級下冊“年、月、日”時，根據學生已有的年、月、日生活經驗，課前教師讓學生思考這兩個問題：（1）二月的天數為什么最少？（2）七月和八月為什么連續兩個月是大月？教學中，教師利用課件展示古羅馬儒略歷法的故事，讓學生帶著問題聽故事。

問題1：儒略-愷撒最初是怎樣定義大、小月的？全年多少天？（單數的月份定為大月，雙數的月份定為小月，全年366天。）

問題2：366天比365天多1天，怎么辦？（儒略-愷撒認為，二月處決犯人不吉利，希望二月過得快一點，就在二月份里面減去一天，全年是365天。）

問題3：為什么現在八月是雙月也是大月？又采取了什么辦法？（古羅馬奧古斯特因為自己生日的原因，將八月改為大月，七月和八月就成了連續的兩個大月。這樣，全年就共有7個大月，4個小月。31×7=217，30×4=120，217+120=337。337+29=366，又多出一天，還是從二月里扣除，這樣二月就變成了28天。）

教學中，教師展示儒略歷法的故事，學生參與學習的熱情得以激發出來，對年、月、日的學習多了一份歷史的厚重感，抽象枯燥的年、月、日知識也變得有溫情。通過有趣的故事突破新知難點，學生對年、月、日也就加深了理解。

二、借鑒經典操作，掌握新知重點

剪切、拼寫、折疊等手腦并用的過程是一個再創造的過程，是以實際問題為出發點，經過系列的操作、分析、提煉，抽象出一般的數學原理、原則及方法，從而實現解決同類問題的過程。根據兒童的天性與成長規律，學生要想將課堂所學的知識內化成自己的知識，形成自己的見解，提高學習能力，必須自己動手操作，手腦并用。數學史料中記載著許多經典的學習操作法。在教學中，基于兒童動作思維的認知特點，教師要不露痕跡地把歷史經典操作場景帶到學生面前，喚醒兒童的活動經驗，引導學生跟著經典進行表象操作，思考這種經典操作法與自己方法的異同，由此理解數學原理，掌握知識重點，增強思維的靈活度。

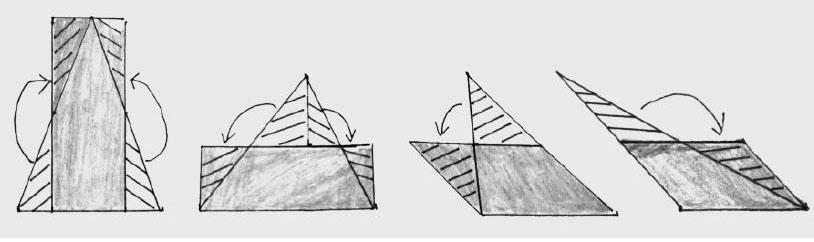
例如，在教學人教版數學五年級上冊“三角形的面積”時，學生依據教材提示，將兩個完全相同的三角形拼成平行四邊形，通過尋找拼成的平行四邊形與三角形的各部分關系，初步推導得出三角形面積的計算公式。這時，教師利用多媒體介紹《九章算術》中記錄的“出入相補”數學原理，鼓勵學生跟著史料介紹的“多余補不足”的操作法，進行分組操作研究（如下圖），邊操作邊記錄，再分層口述操作的發現。

學生在從實物操作到借鑒經典進行操作的活動環節中，輕松尋找出計算平面圖形的面積規律，個性思維得以充分展示，認知結構得以完善，明白了“出入相補”原理與轉化思想運用有著本質上的聯系。三角形轉化成平行四邊形（或長方形）后，兩者之間的等量關系是推導平面圖形面積計算公式的“根本”，而懂得為什么要沿著高或高的一半或腰的一半剪拼，為什么要轉化成平行四邊形（或長方形），則是推導三角形面積計算公式的“靈魂”，“根本”是顯性的，“靈魂”是隱性的。學生會慢慢地淡忘數學知識，但是數學活動經驗、數學方法思想卻能幫助學生理解掌握新知重點，提升數學核心素養，讓學生終身受用。

三、再現數學名題，突破新知難點

數學名題是古人用數學知識去解決問題的智慧結晶。正如數學家波利亞所言：“只有理解人類如何獲得某些事實或概念的知識，我們才能對人類的孩子應該如何獲得這樣的知識做出更好的判斷。”人教版數學教科書常以介紹什么人、什么時候創造的數學成就來呈現數學史實。在教學中，教師要充分考慮兒童的身心發展規律、經驗、情感等，結合兒童的思維特點，通過設計合理的教學環節，再現數學名題，幫助兒童找準解決數學問題所需的各個知識點的聯系與區別，引導兒童學會面對新知聯想舊知，從一種方法遷移到另一種方法。數學名題的篩選和使用，會讓兒童將所學的知識與方法前后貫通，真正理解各種知識與方法之間嚴謹的邏輯關系，進而突破知識難點，降低學習難度，提高課堂教學效率。

例如，在教學人教版數學四年級下冊“雞兔同籠”問題時，教師在學生學會用畫圖法、列表法、假設法解決簡單的“雞兔同籠”問題后，適時引入古代《孫子算經》中的“雞兔同籠”原題，學生積極參與古人解題方法的探究過程，猜想得出：（1）先假設讓雞抬起1只腳，兔子抬起2只腳，還有94÷2=47（只）腳。這時地上的兔子腳數比雞腳數多1，腳與頭的總數之差為47-35=12，兔子的只數就是12。（2）假設雞與兔子同時抬起2只腳，這時還剩下94-35×2=24（只）腳，雞屁股著地，只有兔子的2只腳在地上，有24÷2=12（只）兔子，有35-12=23（只）雞。（3）假設讓兔子抬起2只腳，35×2=70（只）腳，腳數和原來差94-70=24（只）腳，這24只腳正是每只兔子抬起的2只腳的總和，有24÷2=12（只）兔子，有35-12=23（只）雞。以上三種形式的“抬腳法”不必要求學生一一猜想得出，只需引導學生觀察對比《孫子算經》中講解的“抬腳法”與自己掌握的三種方法之間的聯系與區別。通過比較、思考、溝通，學生發現畫圖法和列表法實際上就是假設法的基礎，“抬腳法”其實也是假設法，都要通過假設、計算、推理、調整，最后得出結論，實際上都是蘊含假設的思想方法，只要找準雞的只數、兔子的只數與腳數的變化規律，變抽象為直觀，就能形成牢固的認知結構。數學名題的再現激發了學生學習興趣，學生被數學名題蘊含的邏輯性所吸引，學生充分展開聯想，尋找聯結點，把握知識的來龍去脈，不但難點得以突破，數學知識也學得更深厚。

數學史對兒童的教育價值是多方面的，在數學教學中，教師要基于兒童視角，以兒童為中心，在教學實踐中注意積累，用心關注，用心研究，巧妙選擇，有效滲透數學史。在數學史文化的滋養下，學生能增長知識，發展技能，升華情感，活躍思維，學會更加理性地對待數學問題，逐步提升數學核心素養。

（作者單位：福建省莆田市涵江區國歡中心小學）

本文系教育部福建師范大學基礎教育課程研究中心2019年開放課題“基于兒童立場的小學數學課堂教學策略的研究”（課題批準號KCX-2019061）階段性研究成果。