整體視角下的初中數(shù)學(xué)復(fù)習(xí)課教學(xué)

張維

[摘? 要] 文章以整體教學(xué)的課堂設(shè)計(jì)為載體，重視學(xué)生知識(shí)的整體構(gòu)建，引領(lǐng)學(xué)生深度思考，形成知識(shí)體系，為后續(xù)學(xué)習(xí)奠定堅(jiān)實(shí)的基礎(chǔ)，為后續(xù)的發(fā)展提供持續(xù)的動(dòng)力.

[關(guān)鍵詞] 整體教學(xué);復(fù)習(xí);教學(xué)設(shè)計(jì)

復(fù)習(xí)課是回顧、組織與運(yùn)用的一個(gè)綜合過程. 而復(fù)習(xí)課中最重要的知識(shí)回顧不應(yīng)該只是點(diǎn)狀的、孤立的復(fù)述過程，更多地應(yīng)從學(xué)科內(nèi)涵與價(jià)值角度出發(fā)，指向?qū)W習(xí)結(jié)果發(fā)生發(fā)展規(guī)律，將知識(shí)串聯(lián)在一起，最終形成結(jié)構(gòu)化的知識(shí). 因此我們的復(fù)習(xí)課教學(xué)設(shè)計(jì)應(yīng)充分考慮與小學(xué)已學(xué)知識(shí)的聯(lián)系，通過知識(shí)遷移、類比來復(fù)習(xí)與梳理初中相關(guān)知識(shí)，最終為高中及后續(xù)的學(xué)習(xí)服務(wù).

整體構(gòu)建相對(duì)完整是數(shù)學(xué)學(xué)科的重要特點(diǎn)，章建躍老師特別強(qiáng)調(diào)數(shù)學(xué)教學(xué)應(yīng)該重視其整體性. 《數(shù)學(xué)課程標(biāo)準(zhǔn)》對(duì)整體性教學(xué)也提出了具體的要求：我們的教學(xué)要注重知識(shí)的生長與延伸，將各知識(shí)置于整體框架中并注重內(nèi)在聯(lián)系，處理好知識(shí)點(diǎn)之間的關(guān)系，引導(dǎo)學(xué)生感受數(shù)學(xué)整體美.

整體性復(fù)習(xí)課教學(xué)應(yīng)注意的幾個(gè)問題

復(fù)習(xí)課教學(xué)過程中容易忽視知識(shí)內(nèi)在的關(guān)聯(lián)性，輕視知識(shí)的形成與發(fā)展過程中的邏輯關(guān)系，不重視知識(shí)在整個(gè)教材體系中的地位和作用，出現(xiàn)“只見樹木，不見森林”的教學(xué)狀態(tài)，以致學(xué)生孤立所得的知識(shí)碎片而不能正確地應(yīng)用到整體任務(wù)中，導(dǎo)致學(xué)習(xí)遷移度低. 所以我們的復(fù)習(xí)課要有整體架構(gòu)，設(shè)計(jì)要注重整體性. 那什么是整體性教學(xué)設(shè)計(jì)？目前，還沒有形成一個(gè)統(tǒng)一的定義，結(jié)合學(xué)者觀點(diǎn)筆者認(rèn)為，整體教學(xué)設(shè)計(jì)是構(gòu)建結(jié)構(gòu)的“系統(tǒng)”相關(guān)知識(shí)，以“學(xué)習(xí)中心”用已掌握的知識(shí)輔助學(xué)習(xí)新知識(shí)、解決新問題，將相同結(jié)構(gòu)的內(nèi)容關(guān)聯(lián)思考、整體設(shè)計(jì). 從整體性角度來看，以構(gòu)建知識(shí)為目的，教師對(duì)學(xué)生進(jìn)行有效的自我探索指導(dǎo)，這是教學(xué)設(shè)計(jì)完整性的核心. 那么在教師的精心指導(dǎo)下，如何將學(xué)生已獲取的基礎(chǔ)知識(shí)和基本方法運(yùn)用到陌生的情境中去，進(jìn)而實(shí)現(xiàn)有效遷移，便成為數(shù)學(xué)教學(xué)開展整體性教學(xué)的必要途徑.

整體視野下的復(fù)習(xí)課教學(xué)設(shè)計(jì)必然關(guān)注知識(shí)的整體、結(jié)構(gòu)和關(guān)聯(lián).

1. 整體性

（1）目標(biāo)的整體性

《數(shù)學(xué)課程標(biāo)準(zhǔn)》從“知識(shí)技能、數(shù)學(xué)思考、問題解決、情感態(tài)度”四個(gè)維度進(jìn)行闡述，它們是密切聯(lián)系、相互交融的整體. 我們的復(fù)習(xí)課教學(xué)設(shè)計(jì)要始終關(guān)注四項(xiàng)目標(biāo)的達(dá)成，始終關(guān)注“數(shù)學(xué)素養(yǎng)”這一總目標(biāo)的達(dá)成，所以教學(xué)設(shè)計(jì)要圍繞目標(biāo)整體性展開.

（2）教學(xué)的整體性

初中數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計(jì)是通過整體構(gòu)建教學(xué)來實(shí)現(xiàn)的. 整體教學(xué)本身是一種整體存在，整個(gè)教學(xué)過程始終圍繞“整體”展開. 我們的教學(xué)設(shè)計(jì)應(yīng)擺脫片段的、孤立的教學(xué)模式，關(guān)注各部分與知識(shí)結(jié)構(gòu)之間的緊密聯(lián)系. 構(gòu)建復(fù)習(xí)課時(shí)，教師應(yīng)始終強(qiáng)調(diào)知識(shí)間的內(nèi)在聯(lián)系，通過思想、方法等主線貫通知識(shí)模塊，在聯(lián)系中層層遞進(jìn)，整體構(gòu)建學(xué)生的知識(shí)框架與認(rèn)知結(jié)構(gòu). 對(duì)于學(xué)生的認(rèn)知結(jié)構(gòu)，我們要幫助其建立知識(shí)框架，整體構(gòu)建，因此，我們的教學(xué)必須注重整體性.

2. 結(jié)構(gòu)性

“結(jié)構(gòu)性”更大程度上是由數(shù)學(xué)課程本身所決定的. 幫助學(xué)生有效構(gòu)建合理的認(rèn)知結(jié)構(gòu)是教學(xué)的根本任務(wù). 因此，我們的教學(xué)設(shè)計(jì)始終圍繞“結(jié)構(gòu)性”展開，設(shè)計(jì)促進(jìn)學(xué)生建構(gòu)合理的知識(shí)構(gòu)建的結(jié)構(gòu)化學(xué)習(xí)資源. 它主要表現(xiàn)在以下幾個(gè)方面：

（1）數(shù)學(xué)知識(shí)結(jié)構(gòu)性

數(shù)學(xué)知識(shí)之間總是存在著千絲萬縷的聯(lián)系，知識(shí)本身的邏輯性造就了知識(shí)之間固有的內(nèi)在聯(lián)系. 數(shù)學(xué)知識(shí)既包括“客觀性知識(shí)”，也包括“主觀性知識(shí)”. 數(shù)學(xué)的思想、方法、規(guī)律使數(shù)學(xué)知識(shí)之間實(shí)現(xiàn)了很好的貫通. 我們的數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計(jì)要緊緊圍繞“數(shù)學(xué)知識(shí)結(jié)構(gòu)”這一主題展開.

（2）數(shù)學(xué)認(rèn)知結(jié)構(gòu)性

奧蘇貝爾的研究表明，教材知識(shí)構(gòu)建是學(xué)生數(shù)學(xué)認(rèn)知結(jié)構(gòu)形成的基礎(chǔ). 學(xué)生的數(shù)學(xué)知識(shí)要經(jīng)歷重新組織和融合來納入原有的知識(shí)結(jié)構(gòu)中，所以我們的復(fù)習(xí)課教學(xué)設(shè)計(jì)要圍繞數(shù)學(xué)認(rèn)知結(jié)構(gòu)展開，要幫助學(xué)生造就屬于自己的數(shù)學(xué)認(rèn)知結(jié)構(gòu). 初中生的認(rèn)知結(jié)構(gòu)還未達(dá)到螺旋上升，所以教學(xué)設(shè)計(jì)要針對(duì)數(shù)學(xué)認(rèn)知結(jié)構(gòu)性.

（3）數(shù)學(xué)教學(xué)結(jié)構(gòu)化

整體教學(xué)的整體性不僅僅體現(xiàn)在“整體”的教學(xué)思路上，還體現(xiàn)在整個(gè)復(fù)習(xí)教學(xué)的結(jié)構(gòu)性上. 正因?yàn)檫@種結(jié)構(gòu)性的存在，才保證了教學(xué)的整體性存在. 教學(xué)過程的各個(gè)方面是密切相關(guān)的結(jié)構(gòu)，緊扣每個(gè)結(jié)構(gòu)與整體的關(guān)系使其形成一個(gè)緊固結(jié)構(gòu). 同時(shí)，教學(xué)的結(jié)構(gòu)化是實(shí)現(xiàn)學(xué)生數(shù)學(xué)知識(shí)結(jié)構(gòu)化、數(shù)學(xué)認(rèn)知結(jié)構(gòu)化的保障.

3. 關(guān)聯(lián)性

聯(lián)系是分割的結(jié)果，如果沒有分割，就沒有聯(lián)系，而過度分割卻會(huì)讓數(shù)學(xué)知識(shí)變得零星、細(xì)碎. 數(shù)學(xué)教學(xué)總是期望通過零星、細(xì)碎的知識(shí)使學(xué)生的學(xué)習(xí)變得簡(jiǎn)單明了. 但問題是，分割直接導(dǎo)致割裂和孤立，分割的知識(shí)、分割的教學(xué)使學(xué)生頭腦中的知識(shí)變得零星、細(xì)碎，難以重新組裝在一起，導(dǎo)致調(diào)用不靈活，不能舉一反三，難以融會(huì)貫通，這正是低效復(fù)習(xí)課的癥結(jié)所在. 初中數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計(jì)，重在幫助學(xué)生回到整體，即便是部分的學(xué)習(xí)，也應(yīng)將知識(shí)置于系統(tǒng)之中，在系統(tǒng)的整體輪廓下理解部分. 分割是還原論慣用的手段，只有關(guān)聯(lián)才能使分割后的部分再次“還原”為整體.

關(guān)聯(lián)性特征是“整體性”“結(jié)構(gòu)性”的根本. 因此，關(guān)聯(lián)性是初中數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計(jì)的核心特征，缺少了關(guān)聯(lián)，整體也便不復(fù)存在了. 鑒于上述特點(diǎn)，我們的復(fù)習(xí)課教學(xué)設(shè)計(jì)應(yīng)遵循一定的流程：首先將問題情境形成和同化成新的對(duì)象，接著由先行組織者進(jìn)行類比獲得整體認(rèn)識(shí)，整體認(rèn)識(shí)包含研究對(duì)象、研究過程和研究方法，然后進(jìn)行局部研究，以問題為載體，以過程為主線，以方法為指導(dǎo)，最后構(gòu)建知識(shí)體系，達(dá)到整體效果.

我們的教學(xué)設(shè)計(jì)只有注重整體性、結(jié)構(gòu)性和關(guān)聯(lián)性，才是高效的教學(xué)設(shè)計(jì)，才能更好地為教學(xué)服務(wù)，為學(xué)生服務(wù).

構(gòu)建以生為本的整體性復(fù)習(xí)課

教學(xué)設(shè)計(jì)路徑

1. 借前測(cè)，憶舊知

為了了解學(xué)情，設(shè)計(jì)“直角三角形”復(fù)習(xí)的前測(cè)問題4題如下.

1. 在Rt△ABC中，直角邊AC=2 cm，BC=3 cm，那么斜邊AB的長度為（? ? ? ）

A. 1 cm? ? ? ? ? B. 5 cm

C. cm? ? ? D. ?cm

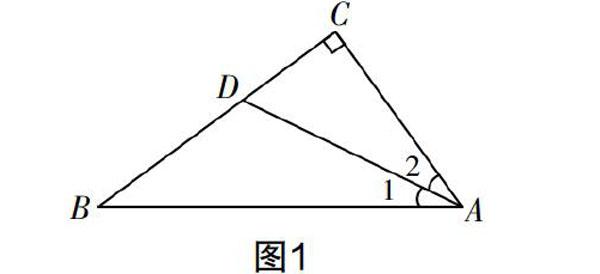
2. 如圖1，在Rt△ABC中，∠ACB=90°，AD平分∠BAC交BC于點(diǎn)D. 如果BC=8 cm，BD=6 cm，那么點(diǎn)D到AB的距離為（? ? ？搖 ）

A. 1 cm? ? ?B. 2 cm

C. 2?cmD. 3 cm

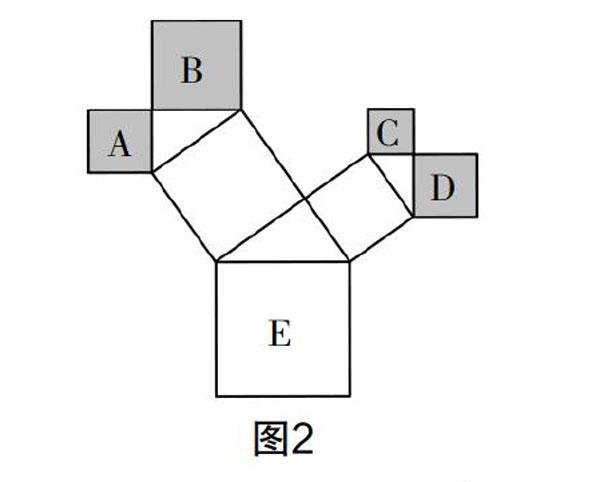
3. 如圖2，勾股樹中正方形A，B，C，D的面積分別為4 cm2，8 cm2，2 cm2和4 cm2，則最大的正方形E的面積為________cm2.

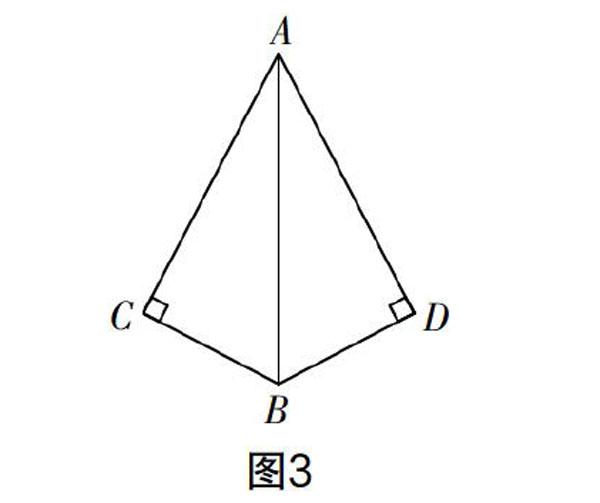
4.如圖3，若只添加一個(gè)條件，就能運(yùn)用“HL”來判定Rt△ABC與Rt△ABD全等，則添加的條件是______.

設(shè)計(jì)意圖通過前測(cè)，復(fù)習(xí)直角三角形的基本知識(shí)：勾股定理、直角三角形全等的證明等，以達(dá)到憶舊知的目的.

2. 練雙基，促提升

問題1：如圖4，給出Rt△ABC，你能得出哪些結(jié)論？這些結(jié)論有什么特殊性？

設(shè)計(jì)意圖 借助問題，回憶直角三角形的相關(guān)知識(shí)，但此時(shí)的知識(shí)是散狀的、點(diǎn)狀的，我們應(yīng)該從邊、角的方向引導(dǎo)、歸納，便于學(xué)生形成知識(shí)結(jié)構(gòu).

3. 解原題，提新問

（添加一個(gè)條件后再解題）

問題2：如圖5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6.

（1）求△ABC的面積;

（2）過點(diǎn)C作CD⊥AB，垂足為D，求CD的長.

設(shè)計(jì)意圖從定義和性質(zhì)（邊、角）兩方面進(jìn)行歸納.

問題3：（1）如圖5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，點(diǎn)D是AB邊上一個(gè)動(dòng)點(diǎn)，則線段CD的取值范圍是多少？

（2）如圖5，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，點(diǎn)D在AB邊上，當(dāng)CD為∠ACB的平分線時(shí)，求CD的長.

（3）如圖6，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，點(diǎn)G在AC邊上，當(dāng)BG為∠ABC的平分線時(shí)，求BG的長.

設(shè)計(jì)意圖 通過問題3，引導(dǎo)學(xué)生對(duì)三種特殊線段進(jìn)行復(fù)習(xí)，注重方法的積累與提升.

4. 煉精華，拓思維

問題4：如圖7，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，AC邊上有一個(gè)動(dòng)點(diǎn)G. 沿直線BG將△BGA翻折到△BGA′，A′B與AC交于點(diǎn)E，當(dāng)AG為何值時(shí)，△A′GE為直角三角形？

設(shè)計(jì)意圖讓學(xué)生從特殊線的角度構(gòu)建知識(shí)體系. 熟悉直角三角形中三條新的特殊線是指斜中線=，斜高=和角平分線，原有知識(shí)結(jié)構(gòu)進(jìn)一步完整.

5. 重今生，續(xù)來世

通過對(duì)稱軸，于橫向，可由直角三角形知識(shí)過渡到等腰三角形，而等腰三角形的復(fù)習(xí)也可以從定義、性質(zhì)、判定三個(gè)角度來形成框架;于縱向，過渡到平行四邊形、矩形、菱形、正方形，仍用定義的屬性轉(zhuǎn)換，再從邊、角、特殊線三個(gè)方向深入串聯(lián)，最終形成知識(shí)體系. 從而達(dá)到直角三角形到等腰三角形，以及三角形到四邊形的整體架構(gòu)，達(dá)到幾何圖形認(rèn)識(shí)“重今生，續(xù)來世”的目的.

結(jié)束語

注重教學(xué)設(shè)計(jì)的整體性，正如章建躍所說：教學(xué)建立在前后一致、合乎邏輯和連貫的學(xué)習(xí)過程中，使學(xué)生在掌握知識(shí)的同時(shí)學(xué)會(huì)思考，使學(xué)生有知識(shí)的整體把握，能夠?qū)⒘闵⒅R(shí)進(jìn)行關(guān)聯(lián)與整合，友好延伸形成合理而良好的知識(shí)結(jié)構(gòu)，進(jìn)而生長、豐富新的認(rèn)知結(jié)構(gòu)，使發(fā)展學(xué)生的學(xué)習(xí)力和創(chuàng)新力能在復(fù)習(xí)課堂上有效落實(shí).

因此，我們的學(xué)習(xí)過程要強(qiáng)調(diào)構(gòu)建有層次的思維，解決拓展類問題. 整體性教學(xué)設(shè)計(jì)的實(shí)施要幫助學(xué)生避免因知識(shí)結(jié)構(gòu)缺乏認(rèn)識(shí)而產(chǎn)生孤立、分割的散狀學(xué)習(xí);要幫助學(xué)生避免“未能顧及知識(shí)的前后聯(lián)系”而將教學(xué)內(nèi)容以點(diǎn)狀形式進(jìn)行傳遞;要幫助學(xué)生進(jìn)行有效的學(xué)習(xí)，提升數(shù)學(xué)品質(zhì)和素養(yǎng);要幫助學(xué)生在后續(xù)的學(xué)習(xí)過程中奠定堅(jiān)實(shí)的知識(shí)和能力.