借助幾何圖形　豐富直觀體驗

白宗化

“幾何直觀”作為《義務教育數學課程標準（2011年版）》的核心概念之一，在數學學習中有重要的地位和意義。“幾何”即幾何圖形。“直觀”就是借助經驗、觀察、測試或類比聯系，所產生的對事物關系的直接的感知與認識，通過直觀能建立起學生對自身體驗與外物體驗的對應關系。在實際教學中，幾何直觀可以把復雜的問題變得簡明、形象，有助于探索解決問題的思路，預測結果。本期，我們來討論如何提高學生的幾何直觀能力。

幾何直觀是依托、利用圖形進行數學的思考和想象。它既是一種意識，也是一種能力和思維方式。教師可以借助幾何圖形，幫助學生理解數學，豐富直觀體驗。

一、借助幾何之形，表達代數之意

借助于幾何直觀，不僅可以讓抽象的代數問題變得直觀，而且可以讓抽象的代數算法、算理得到生動的詮釋和展現。

在教學《絕對值》時，筆者首先創設情境并提問：如下圖，兩只小狗和一頭大象在同一直線上，兩只小狗距離原點有多遠？大象距離原點有多遠？

生1：小狗距離原點都是3個單位，大象距離原點4個單位。

師：兩只小狗和大象在數軸上表示的有理數分別是多少？

生2：兩只小狗表示的有理數分別是-3和+3，大象表示的有理數是+4。

師：一般數軸上表示數a的點與原點的距離叫作數a的絕對值，記作|a|。比如，這里|-3|=3，|+3|=3。你能說出|4|是多少嗎？

生（齊）：是4。

師：0的絕對值是多少？為什么？

生3：是0，因為0到0的距離是0。

師：說得真好！通過“絕對值”的定義，我們可以發現，任何一個有理數的絕對值都是正數或0，因為絕對值表示的是這個數到原點的距離，而距離是不可能為負數的。

筆者借助數軸，創設一個問題情境，讓學生感知“距離是正數”，然后引導學生觀察它們所表示的有理數中有正數也有負數。這種“由數到形、由形想數”的過程，使學生建立了數形之間的聯系。

二、借助幾何圖形，證明公式定理

利用幾何圖形，可以證明數學中的很多公式、定理和法則。這樣數形類比，能加深學生對公式、定理的理解。

筆者在教學《勾股定理》時，就嘗試讓學生用“趙爽弦圖”來驗證勾股定理的正確性。

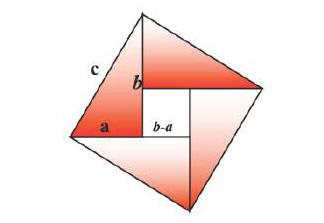
師：下圖中，大正方形的面積可以怎樣表示？

生1：c2。

師：再仔細觀察一下，還可以怎樣表示？

生2：還可以用4個直角三角形的面積加1個小正方形的面積。

師：它們相等嗎？為什么？

生3：相等，因為它們都表示大正方形的面積。

師：列出這個等式，看看你發現了什么？

學生在草稿紙上列出等式，展開、化簡后發現“a2+b2=c2”，感覺非常神奇。接著，筆者介紹了另外幾種圖形，鼓勵學生嘗試用面積來證明勾股定理。利用圖形來證明公式定理，有助于學生打通數形的“任督二脈”，實現了數形之間的有效轉換。

三、實施動手操作，培養空間想象

初中數學教學中，教師可以有計劃、有目的地組織學生利用相關工具（如白紙、剪刀、測量工具、實物、計算機等）進行折、剪、拼、測、畫等操作活動，然后通過觀察、分析、猜想、歸納等思維活動，獲得數學知識的感性認識，達到直觀體驗的目的。

例如，在學習《立體圖形與平面圖形》時，筆者設計了如下操作活動。

（1）如下左圖，把準備好的墨水瓶包裝盒裁剪并展開，并在小組中進行交流。

（2）如下右圖，觀察展開圖，看看它的展開圖由哪些平面圖形組成，再把展開的紙板復原為包裝盒，體會立體圖形與平面圖形的關系。

這樣教學，學生在裁剪、展開和還原的操作活動過程中，發現一個長方體（或正方體）的平面展開圖具有多樣性。小組討論、總結發現一共有11種情況：1-4-1型的有6種（圖1），1-3-2型的有3種（圖2），3-3型和2-2-2型各1種（圖3，圖4）。

學生在操作活動的過程中，體會到了平面圖形與立體圖形之間的聯系和區別，提升了幾何直觀和空間想象能力，為后面的數學學習奠定了基礎。

四、培養畫圖習慣，促進數學理解

培養學生的幾何直觀應從畫圖習慣入手，鼓勵學生用圖形進行表達，使學生真正體會到畫圖對理解概念、尋求解題思路帶來的便利。

例如，教學《二次根式的加減》時，在不給出圖形的基礎上，教師出示了如下問題：現有一塊長為7.5dm，寬為5dm的長方形木板，能否在這塊木板上截出兩個面積分別是8dm2和18dm2的正方形木板？

師：你能畫出這個長方形的草圖嗎？（學生在草稿紙上畫圖）請同學們看看老師畫的草圖，如下圖，兩個面積分別是8dm2和18dm2的正方形的邊長分別是多少？

生1：[8]和[18]。

師：它們能截出來嗎？兩個正方形的位置如何擺？

生2：應該橫著擺，豎著擺不出來。

師：為什么擺不出來呢？說出你的理由。

生3：通過估算，兩個數加起來大于5，超過了長方形的邊長。

師：對！我們可以估算出來！那么它們的和到底等于多少呢？這就是我們今天要學習的“二次根式的加減”。

本節課教師通過問題導入，沒有給出圖形。學生自己動手畫圖，并結合圖形進行分析，對無理數[8]和[18]進行化簡、合并，培養了學生根據圖形進行觀察、推理的能力。

初中數學中很多題目是沒有幾何圖形的，這就需要學生進行畫圖分析、推理解決問題，有時候還要進行分類討論。教師在教學中要注重培養學生畫圖分析的能力，促進學生對數學問題的理解與掌握。

（作者單位：荊州市東方紅中學）