復轉矩系數法的一種改進應用方法

付敏 顏世魁 畢妍霜

摘要：為提高電力系統次同步穩定性分析的效率，提出一種基于復轉矩系數法的快速分析方法。考慮到工程實際中缺乏機械阻尼數據，采用了只考慮電氣阻尼的穩定判據。利用PSCAD/EMTDC軟件搭建了IEEE第一標準模型，并基于該系統分析了傳統復轉矩系數法及其早期優化方法的特點，進而提出將頻率掃描法與測試信號法相結合的改進分析方法。改變IEEE第一標準型的串補線路參數，并應用快速分析法對不同穩定性的系統模型分別進行了次同步穩定性分析，最后結合時城仿真驗證了分析結果的有效性。通過實驗驗證，該方法在系統次同步穩定性分析時，相比復轉矩系數法更具時效性。

關鍵詞：次同步振蕩;復轉矩系數法;測試信號法;頻率掃描法

DOI：10.15938/j.jhuSt.2020.02.013

中圖分類號：TM712文獻標志碼：A 文章編號：1007-2683（2020）02-0096-09

0 引言

為提高遠距離輸電系統的傳輸容量、改善系統穩定性，線路串聯補償技術被廣泛應用，但在提高經濟效益的同時，其可能引發的次同步振蕩（Subsyn-chronous Oscillation，SSO）問題，也為電力系統的穩定運行帶來了安全隱患。復轉矩系數法作為分析次同步振蕩問題的主要方法之一，可以快速掃描出待研究系統的電氣阻尼特性，結果精確，有利于工程上對次同步振蕩問題的研究。自1982L M。Canay提出復轉矩系數法以來，國內外對復轉矩系數法進行了大量研究。文提出一種改進簡化的方法，即在注入擾動時，同時加人一串相同幅值、不同頻率的擾動量，并施加一個與頻率相關的滯后相位。文分析了復轉矩系數法與特征值分析法之間的聯系。文提出復轉矩系數法的時域仿真實現方法——測試信號法來進行次同步振蕩分析;文推導了多模式次同步諧振各扭振模式阻尼的顯式表達式，在理論上進一步解析次同步諧振的機理;文利用奈斯特穩定判據給出了復轉矩系數法的證明。本文基于PSCAD/EMTDC軟件搭建了IEEE第一標準模型，并分別從電氣和機械兩部分介紹了復轉矩系數分析法的具體步驟。考慮到工程實際中缺乏機械阻尼實測數據，文中采用只考慮電氣阻尼的穩定判據對系統進行穩定性分析，具體對電氣阻尼分析時，應用了測試信號法，并對比了不同擾動注入方式對分析結果的影響。針對復雜系統仿真時間較長的問題，提出使用頻率掃描法與復轉矩系數法相結合的方式對系統進行快速分析，最后進行了時域仿真驗證。

1 復轉矩系數法

1.1 次同步振蕩概念

有關次同步振蕩（SSO）問題的討論最早始于1937年，經過幾十年的不斷探索和研究，人們對SSO產生的原因和機理已有一定的認識。其產生的原因主要包括：感應發電機效應;暫態扭矩放大;軸系扭轉振蕩和由其他電氣裝置引起的SSO等四個方面。

依據IEEE工作組對SSO的定義，電力系統次同步振蕩是指發電機組在運行（平衡）點受到擾動后出現的一種異常運行狀態，在這種運行狀態下，電氣系統與發電機組之間在一個或多個次同步頻率下進行顯著的能量交換，從而危害汽輪發電機軸系的安全運行。

1.2 復轉矩系數法原理

對于電力系統來說，機械系統與電氣系統之間，除了通過發電機電磁轉矩△t.和轉子角度△δ（轉子角速度△ω）相互聯系之外，無其他直接聯系。復轉矩系數法的基本思想是將系統的電氣部分和機械部分分別進行研究。Canay在文中將系統電氣部分和機械部分的線性化微分代數方程分別列寫，并消去除△δ和△ω之外的其他變量，可得到用微分算子s表示的轉矩偏差△t.與△δ和△ω之間的關系

式中：K_e（s）為電氣復轉矩系數;K_m（s）為機械復轉矩系數，他們都是微分算子s的有理分式。令s=jω，可得K_e（s）和K_m（s）對應的頻響特性K_e（jω）和K_m（jω），設：

式中，K_e和D_e分別稱為電氣彈性系數（或電氣同步轉矩系數）和電氣阻尼系數（或電氣阻尼轉矩系數）;K_m和D_m分別稱為機械彈性系數（或機械同步轉矩系數）和機械阻尼系數（或機械阻尼轉矩系數）。

在發電機轉子上施加一角頻率為h的小幅振蕩。即：

通過分析K_e、D_e、K_m、D_m在次同步頻率范圍內隨頻率變化的情況，可對系統的次同步穩定性進行判斷。

復轉矩系數法判斷次同步振蕩穩定性的準則為：

對于K_e（h）+K_m（h）=0的頻率點h，

若D_e（h）+D_m（h）=0，系統臨界穩定;

若D_e（h）+D_m（h）<0，系統不穩定;

若D_e（h）+D_m（h）>0，系統穩定。

由于機械系統的彈性系數遠大于電氣系統的彈性系數，可以認為K_e（h）+K_m（h）=0的頻率點非常接近K_e（h）=0的頻率點，即軸系的自然扭振頻率點。因此，次同步振蕩穩定性的準則可變為：

若對于發電機所有軸系自然扭振頻率點f都有：

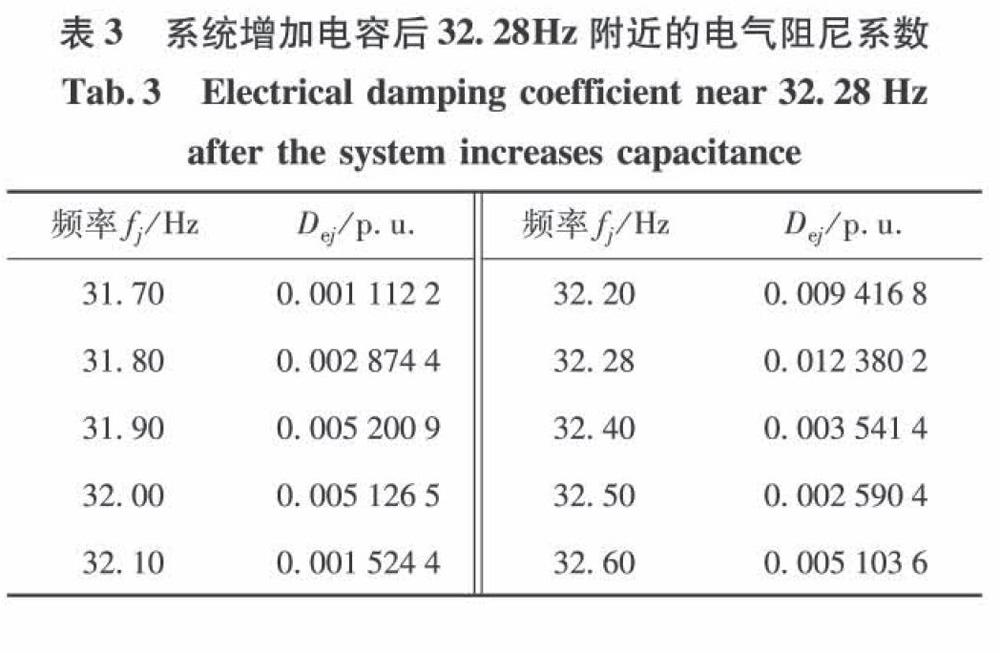
D_ej+D_mj>0（5）

則系統不會發生次同步振蕩。若有一個頻率點的電氣阻尼和機械阻尼之和為負，則系統存在SSO問題。