車用內置式永磁電機損耗最小簡易控制

林立 彭正苗 萬炳呈 陳鴻蔚 陳紅專

摘要：為解決車用內置式永磁電機恒功率寬調速效率優化控制中鐵損及飽和電感時變問題，提出一種內置式永磁電機損耗最小簡易控制策略。該策略采用內置式永磁電機近似損耗模型，計及鐵損時變和電感飽和時變對系統性能的影響，得到損耗最小效率優化控制的條件。仿真及實驗結果表明，所提方法控制實現簡單有效、效率更高，節能效果更好，在新能源電動汽車上有較好的應用價值。

關鍵詞：電動汽車;內置式永磁電機;鐵損;飽和電感;效率優化;損耗最小控制

DOI：10.15938/j.jhust.2020.02.012

中圖分類號：TM351文獻標志碼：A 文章編號：1007-2683（2020）02-0088-08

0 引言

提高內置式永磁同步電機效率，節約能源的控制方法有i_d=0控制、恒功率因數控制、最大轉矩比電流控制、損耗最小控制等。其中，損耗最小控制分為基于在線搜索的控制和基于模型的控制兩種。基于在線搜索的控制，其控制變量將根據具體的算法，減少輸入功率或永磁電機的損耗，實現節能控制，該方法不依賴永磁電機參數，但迭代時間長;基于模型的控制方法，原理簡單，動態響應速度快，最優控制時無震蕩，但在實施最優控制時參數依賴性強。在基于模型的控制方法中，利用永磁電機參數得到關于速度和電流i_q的最優控制電流i_d，需脫機操作，導致無法在新能源電動汽車中廣泛應用，此外，在內置式永磁同步電機中，因交叉飽和而引起的電感變化和由于頻率改變而引起的鐵損電阻變化，也對最優勵磁電流i_d產生明顯影響。為解決這一問題，本文提出一種基于損耗模型的損耗最小簡易控制新方法，控制實現簡單，系統控制不嚴格依賴電機參數，效率更高。仿真和實驗驗結果表明所提控制策略具有明顯的優勢，這種新的控制策略對于新能源電動汽車節能控制，提高一次充電續行里程具有重要意義。

1 損耗最小控制

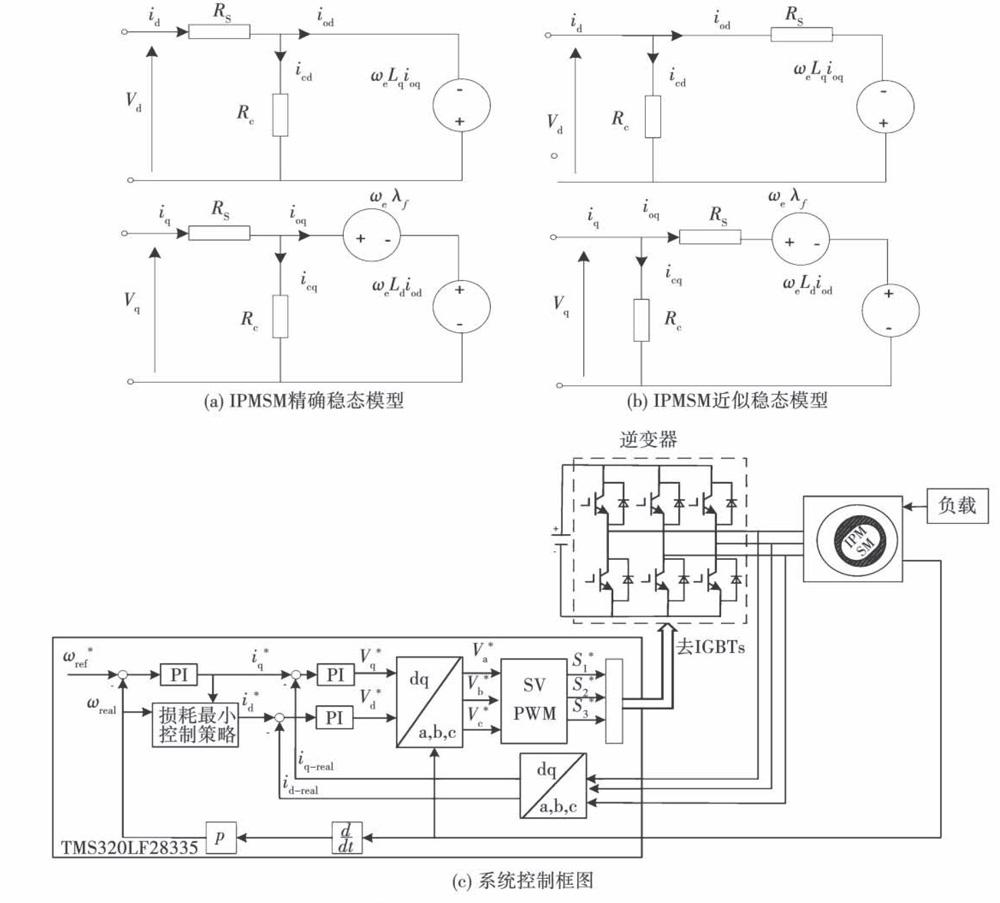
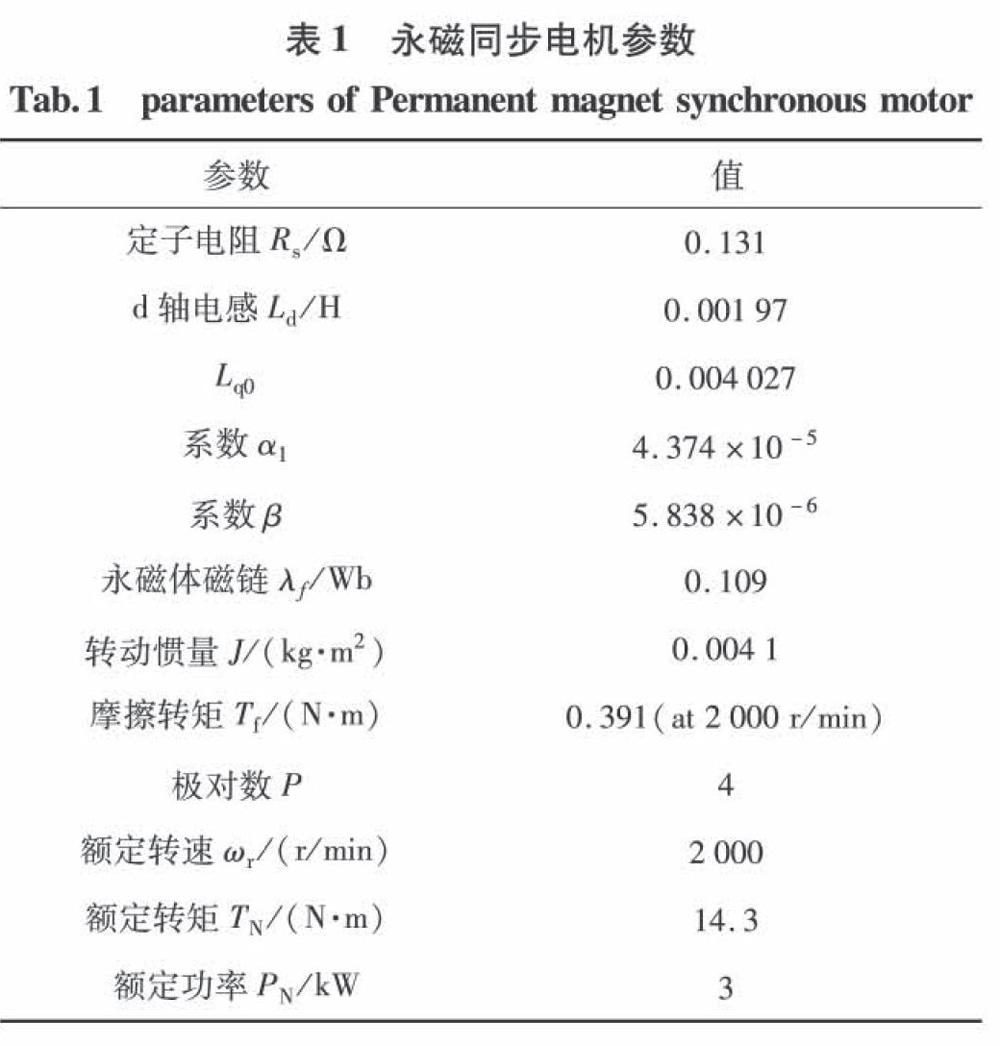
車用內置式永磁同步電機經常運行在恒功率寬調速過程中，存在鐵心損耗（包括磁滯損耗和渦流損耗），特別是電動汽車高速巡航高頻運行時，鐵心損耗不容忽略，基于dq軸模型得到的MTPA控制，效率不是最優的，為提高系統效率，必須考慮鐵損的影響，因此，考慮鐵心損耗的內置式永磁同步電機數學模型如圖1所示。

據圖1等效電路及控制系統框圖，對于表貼式永磁同步電機，考慮鐵損時，由圖1（a）數學模型，損耗最小損耗控制策略，實現條件很容易滿足：式中：ω_e為轉子電角速度;R_s為定子電阻;R_c為鐵耗電阻。該控制策略考慮了鐵心損耗對系統效率的影響，比較準確的對永磁同步電機實施效率最優控制。但對于內置式永磁同步電機，因L_d≠L_q，實現損耗最小控制的條件復雜，難以有效實現，現分析如下，首先依據圖（1a），計算得到總損耗P_總=銅損P_cu+鐵損P_Fe：

式（6）是一個關于i_od，i_oq和ω_e的函數，直接求解是比較困難的。而且，鐵損電阻R_c會隨著速度ω_e的變化而變化，L_q會隨著電流的變化而變化，這些參數不能直接被賦于恒定值，而需要在每一步工作中進行實時計算，才能有效的完成損耗最小控制，因此，從以上分析可知，內置式永磁同步電機的損耗最小控制難以實時有效實現。

2 基于近似損耗模型的損耗最小簡易控制

2.1 內置式永磁同步電機近似損耗模型

為解決內置式永磁同步電機損耗最小控制難以有效實時實現問題，與文所述內置式永磁同步電機精確損耗模型相比，本文提出一種近似損耗模型，以實現損耗最小簡易控制策略，近似損耗模型穩態等效電路如圖1（b）所示，在圖1（b）近似損耗模型等效電路中，鐵損電阻被放在定子電阻及。的前面，2.4節研究表明該近似損耗模型對控制系統性能的影響可以忽略不計。基于近似損耗模型的損耗最小簡易控制控制原理如圖l（c）所示。

從圖l（b）近似損耗等效模型電路可知，銅損和鐵損可分別表示為

比較精確損耗模型和近似損耗模型，精確損耗模型下的d軸控制電壓V_d為

比較基于精確損耗模型推導得到的式（12）和基于近似損耗模型推導得到的式（10）可知：

近似損耗模型可利用式（13）的近似條件進行控制，這一條件在內置式永磁同步電機運行時容易滿足。

在損耗最小控制策略中，一方面，鐵損電阻隨速度的變化而變化，鐵損電阻是關于速度的函數;另一方面，i_d和i_q因轉速和負載變化而變化，考慮到自感及交叉飽和影響，相對于L_d磁路飽和對L_q影響更加明顯，由于直軸所經磁阻路徑的磁導率與空氣近似，所以飽和度對L_d影響較小，交叉飽和對L_q的影響，可用關于L_q的近似線性方程表示為

2.2 損耗最小簡易控制策略

為實現IPMSM運行時損耗最小，穩態時，在恒定轉矩和恒定速度條件下，將總損耗對i_od進行微分求導，并令求導結果為0有：

由于2R_s

式中V_ar（i，ω_e）表示L_q的變化對損耗最小條件的影響，鐵損電阻是關于速度的函數，運用d軸控制電壓V_d和q軸控制電壓V_q可簡化損耗最小控制的條件，并實現損耗最小簡易控制策略，下節將基于式（22）討論分析如何實現損耗最小簡易控制。

2.3 損耗最小簡易控制策略的實現

前述分析指出，基于精確損耗模型的內置式永磁同步電機最小損耗控制，條件復雜，難以實現。式（22）在一定程度上解決了第1個問題，利用PI控制器可解決實現難的問題;PI控制器通過控制i_d使式（22）為零。利用PI控制器直接簡化損耗最小條件，且內存需求小。圖2為所提方法實現的結構框圖，不需要直接測量電壓，而是將控制電路中的dq軸參考電壓等價于內置式永磁同步電機的端電壓;因此，不需要電壓傳感器（PI控制器損耗最小控制條件的相關系數是負值，因為i_d是負值）。根據式（8）、（9）、（22），可用實現，圖2中所用的方程為使用PI控制器的優點之一是可簡化基于Zieder-Nichols算法的系數確定過程。該算法不依賴模型參數，基于Ziegler-Nichols技術，首先，令k_p和k_i均為0;然后，增加K_p，直至出現震蕩。這時，令k_max等于k_p（即在這一點上發生震蕩），令T等于振蕩周期。PI控制器的k_p和k_i最后的結果是k_p=0.45k_max，k_i<=（1.2k_p/T）。

不同PI參數下的結果如圖3所示，在空載條件下，電機從0加速到2000r/min;然后，給永磁電機加載10N·m;對于該方法中的PI調節器的不同參數，由于相同的速度環和電流環控制器，轉速和i_q的響應相同。當k_p數值較小時，i_d緩慢的接近目標值。如圖3a所示，通過適當調節PI控制器的參數，在速度和i_q剛好達到穩態時，在適當的響應時間，i_d可達到最優，也就是說，當速度和i_q是一個指定值時，i_d有一個確定的值相對應，當速度增加時，最優電流值i_d也會相應增加，以滿足該速度條件下的損耗最小。因此，i_d作為一個速度函數，不會使控制器反應緩慢，并且對應不同的速度值有不同的最優i_d。增益越大，則反應速度越快，超調較大，i_d上的超調量在一定程度上是由于i_q的超調引起的（速度控制器），因為最優電流i_d是關于i_q的函數。

2.4 近似損耗模型和精確損耗模型的比較分析

本節對所提近似損耗模型和精確損耗模型控制之間的差異進行比較分析。內置式永磁同步電機的參數如表1所示，在不同i_od和i_op情況下的L_q如圖4b所示。在第2.1節中指出，L_q是關于i_od和i_oq的近似線性函數（為了考慮損耗最小控制中的磁路飽和）。式（14）的系數的近似線性關系如圖4所示。其中，L_d受飽和度變化不大。此外，鐵損電阻R_c是速度的函數，其關系如圖4所示，R_c的測量根據文所提方法測試得到。

圖5是精確損耗模型和近似損耗模型在額定轉速、50%額定轉速及10%額定轉速下效率、銅損和鐵損隨負載轉矩變化的測試曲線。兩個模型的損耗最小控制的效率差小于0.02，基本可以被忽略不計。因此，用近似損耗模型代替精確損耗模型進行控制是可靠的。

3 實驗結果及分析

為驗證所提方法的有效性，在內置式永磁電機半實物仿真平臺上進行了實驗驗證，實驗系統如圖6所示。被測內置式永磁同步電機的參數如表l所示。

實驗時與離線查表最小損耗控制進行比較，計算得到i_od的最優值（i_od是關于速度和i_q的函數），并將其用于查表法中，從而驗證所提近似方法的影響是可以忽略的。該方法與離線查表損耗最小控制法相比，優勢在于本文所提方法是在線的。根據電機方程，并利用i_d，i_q和電機參數，可得電機損耗。通過測量電機參數，據式（2）-（5）可計算電機的不同損耗，飽和度對L_q和頻率對R_c的影響按2.4節所述方法考慮。R_c、機械損耗和雜散損耗、轉矩T_f是速度的函數，可進行測量，在此基礎上，電機工作在恒速和空載狀態下;對于每一個速度，通過改變i_d，據式（24）～（25）計算半輸入功率（輸入功率減去銅損）和速率電動勢的平方。

表2給出電機額定轉速不同控制策略時的總損耗，包括計算法和實驗法得到的銅損、鐵損和機械損耗，兩者結果十分接近。

4 結論

本文提出了內置式永磁電機近似損耗模型損耗最小簡化控制新方法，簡化了損耗最小效率優化控制的條件，不增加硬件成本，有效的減小了微處理器的內存，便于進行實時在線控制，所提方法計及了磁路飽和及等效損耗電阻只。變化對系統性能的影響，所提方法對系統動態性能影響小，能有效降低損耗，實驗結果驗證了所提方法的有效性，在新能源電動汽車上用較好的應用價值。