考慮光、儲、燃聯合發電的微電網優化運行

向紅偉 常喜強 呂夢琳 邢占禮 王晗

摘要：考慮到光伏與負荷的時序相關性，引入廣義負荷作為研究對象，用k-mesns聚類得到微電網運行的典型場景與各個場景對應出現的概率。以年綜合運維成本最小為目標函數，記及功率平衡等約束條件，建立微電網優化運行模型。采用改進的粒子群算法求解，得出并網與孤島兩種運行模式下儲能、電動汽車的充放電策略。最后，以某地區低壓微電網為例，驗證了所提方法與模型的有效性。

關鍵詞：微電網運行;電動汽車;充放電策略

DOI：10.15938/j.jhust.2020.02.010

中圖分類號：TM732文獻標志碼：A 文章編號：1007-2683（2020）02-0073-07

0 引言

隨著高比例分布式電源的接人，電網的電能質量受到了很大的影響，微電網作為消除這一影響的有效途徑之一了研究者的廣泛關注。微電網是集合了分布式電源、儲能單位、負荷以及各種控制單元的小型電網。隨著時代的進步，微電網中增加了很多新的元素，如具有充放電功能的特殊“負荷”一電動汽車。微電網元素的多元化給其安全穩定運行帶來挑戰。因此，如何協調各種資源，使得微電網在并網與孤島兩種情況下運行最經濟，成了研究的重點。

文考慮到直流微電網的時變性與新能源出力的不確定性，提出一種最小化運行成本的直流孤島優化運行策略。文考慮電網的實時電價，協調可控式電源的輸出功率、儲能充放電功率以及微電網與外界交互的功率，提出了微電網在并網狀態下的優化運行策略。文考慮需求側響應，建立了微電網在并網狀態下的多目標優化模型。以上文獻只討論了微電網在孤島或并網這種單一運行狀態下的的優化問題。文通過改變微電網中雙電池儲能系統的充放電策略，不僅拓展了儲能系統的可用容量，還提高了儲能系統的靈活性。文探討了交直流混合微電網中電動汽車充電站的控制策略，雖然分析了兩種運行模式下的控制策略，但優化對象過于單一。文建立了微電網多目標魯棒優化模型，雖然降低了運行的風險，但是由于優化結果過于保守，經濟性下降了很多。文從可靠性、經濟性等四個方面提出了微電網運行的綜合評估方法。

本文首先考慮了光伏機組出力與負荷消納的時序相關性并采用k-means聚類得到微電網運行的典型場景集。其次，以綜合運維成本最小為目標函數，記及功率平衡等約束條件，建立微電網優化運行的數學模型。再次，采用改進的粒子群算法分別求得并網與孤島運行狀態下電動汽車與儲能的充放電策略。最后，以某地區微電網為例，驗證所提優化方法的有效性。

1 場景的選擇

引入廣義負荷的概念，將光伏機組的出力視為負的負荷，與常規負荷合并在一起，稱為廣義負荷。采用k-means對日廣義負荷的均值聚類，得到一組微電網運行的典型場景集以及對應的各個場景在全年出現的概率。

1.1 原始聚類中心的選擇

k-means聚類法原始的聚類中心是隨機確定的，若強制將原本應劃分為同一族的元素作為不同族的聚類中心計算，則會出現聚類結果局部收斂的情況。因此，合理地選取原始聚類中心至關重要。

為了避免聚類結果在局部收斂的情況出現，需要盡可能地分散原始的聚類中心。本文首先將日廣義負荷均值按從小到大的順序排列，然后按樣本數量將其均分為k組，每組元素的均值當作原始聚類中心。

1.2k值的選取

k-means聚類法需要在算法開始前人為地確定好k值，k值取太大會影響模型的求解速度，k值取太小會使聚類得到的典型場景集不能全面地描述一年的運行情況。因此，如何選取合適的k值成了場景選擇過程中最關鍵問題。本文以族內距離與族間距離的和函數L最小時對應的k值作為劃分的總族數，證明過程與具體步驟參考文。

族內距離即所有樣本到各自的族中心的距離之和，用D來表示。族間距離即各族中元素的均值到所有樣本均值的距離之和，用s來表示。綜合距離L為5與D的和函數。具體表達式如下：

式中：i為族的計數;k為聚類劃分的總族數;C_i為第i個族中所有元素的集合;p為第i個族中的元素;m：為第i個族內元素的均值;m₀為所有樣本的均值。

1.3 收斂條件

k-means聚類通過算法迭代，不斷尋找新的聚類中心，直到達到算法的終止條件。聚類算法的收斂條件不僅要考慮到族間的緊密性，同時還要考慮到族間的分散性。所以本文綜合族內與族間距離來確定收斂條件。

采用DBI指標（Davies-Bouldin Index）作為聚類算法的判斷條件。

S（i，j）=||m_i-m_j||（4）

式中：S（i，j）為第i個族與第j個族元素均值的歐式距離;D_i為第i個族內的各個元素到本族元素均值的標準差，N_i為第i個族中元素的個數。

1.4 場景選擇流程

場景選擇的具體步驟如下：

1）將日廣義負荷均值從小到大排列，輸入數據，以及確定的原始聚類中心。

3）選出數組A中的最小值，其對應的k值則為劃分的族數。

4）執行k-means算法，直到滿足DBI指標收斂的條件，跳出算法循環。

5）得到運行典型場景集以及對應場景的概率。

2 模型構建

2.1微型燃氣輪機

微型燃氣輪機的輸出功率與其消耗的天然氣量近似成正比，具體公式如下：

式中：P_MT為m節點第k個場景t時段下微型燃氣輪機的輸出功率，A_na，m，k為m節點第k個場景t時段下消耗天然氣量，η_MT為發電效率，H_MT為微型燃氣輪機熱值。

2.2 蓄電池

儲能裝置以蓄電池為例，蓄電池除了考慮充放電的效率外還要考慮其擱置時容量的自然損耗。另外，為了保證蓄電池的剩余容量在各個場景中具有可連續性，假設容量在各場景末時刻回到初始狀態。式中：S_{Es，m，k，t}為m節點第k個場景t時段下蓄電池的容量，δ為蓄電池自放電的效率，P_{Es，m，k，t}為m節點第k個場景t時段下蓄電池的充放電功率（充電時P_{Es，m，k，t}>0，放電時P_{Es，m，k，t}<0，P_{Es，m，k，t}=0時，蓄電池處于停運狀態），△t為時間間隔，η_es。為充放電效率，P_{battery，m，N}N與S_Es，m，N分別為m節點蓄電池的額定充放電功率和容量。

2.3 電動汽車

電動汽車除了滿足充放電的功率約束外，還需要考慮其在微電網中的充放電時間限制。

式中：P_{Es，m，k，t}為m節點第k個場景t時段下電動汽車的充放電功率（充電時P_{Es，m，k，t}>0，放電時P_{EV，m，k，t}<0，P_{EV，m，k，t}=0時，充電樁上無停靠的電動汽車）S_EV，m，N為m節點上電動汽車的額定充放電功率，t_EV，m為m節點上電動汽車允許充放電的時間范圍，t_s，m與t_e，m分別為m節點上電動汽車允許充放電的起始和結束時間。

2.4 優化模型

本文建立以綜合運維成本最小為目標函數，記及功率平衡等約束的優化模型，分別求得儲能和電動汽車在并網與孤島兩種運行狀態下的充放電策略。

2.4.1 目標函數

優化模型以綜合運維成本最小為目標函數：

minO_total=O_pv+O_Es+O_MT+O_EXC（10）式中：O_total為年綜合運維成本;O_Pv、O_Es和O_MT分別為光伏、儲能和微型燃氣輪機的運維費，O_EXC為微電網與主網的交互費用。其中：

2.4.2 約束條件

1）功率平衡約束

2.5 兩種運行狀態下的控制策略

2.5.1 并網模式

并網運行狀態下，微電網與外界主網相連，無需考慮爬坡約束。此時，目標函數為式（10），約束條件包含式（12）-（15）。

2.5.2 孤島模式

孤島運行狀態下，微電網與外界主網分離，兩者間無功率交互。此時，目標函數為式（10），其中O_ExC=0，約束條件包含式（12）-（14）、（16）。

3 求解算法

利用智能算法可以高效地解決微電網優化這一類非線性優化的問題。傳統的粒子群算法程序簡單，但是可能出現搜索進入局部最優解的情況，因此很多學者對算法進行改進，均取得了較好的求解效果。

因此本文考慮在標準的粒子群算法中融入遺傳算法的思想，避免搜索進入局部最優的情況發生。圖2為求解算法的流程，具體求解步驟如下：

1）隨機選擇一些個體充當初始粒子種群。

2）計算粒子的適應度，在初始種群中暫且把計算結果最高的粒子作為最優解。

3）按粒子群算法進行迭代。

4）將最優個體進行交叉變異。

5）計粒子的適應度，若適應度變大則接受變異進行6），否則不接受此次變異，回到4）重新進行交叉變異。

6）最優群體進行交叉變異。

7）計算粒子的適應度，若適應度變大則接受變異進行8），否則不接受此次變異，回到6）重新進行交叉變異。

8）滿足一定的迭代次數后輸出計算結果，否則回到6）。

4 算例分析

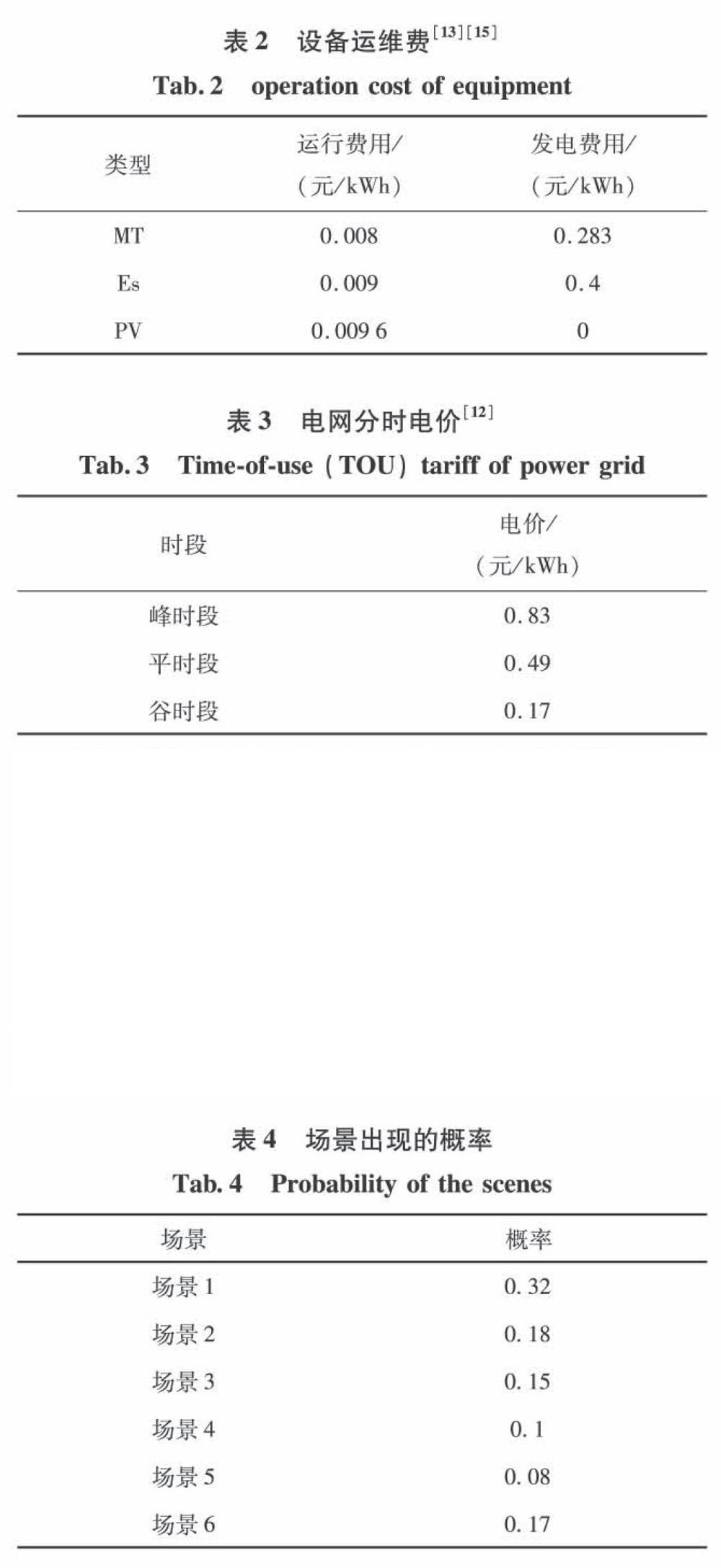
某地區低壓微電網如圖3所示。微電網的具體參數如表1所示。各個設備的運維費見表2，電網峰谷平時段的電價見表3.算例中蓄電池的充放電效率為0.9，自放電效率為0.02，初始時刻的電量為總容量的50%;光伏最大利用小時數為900h。

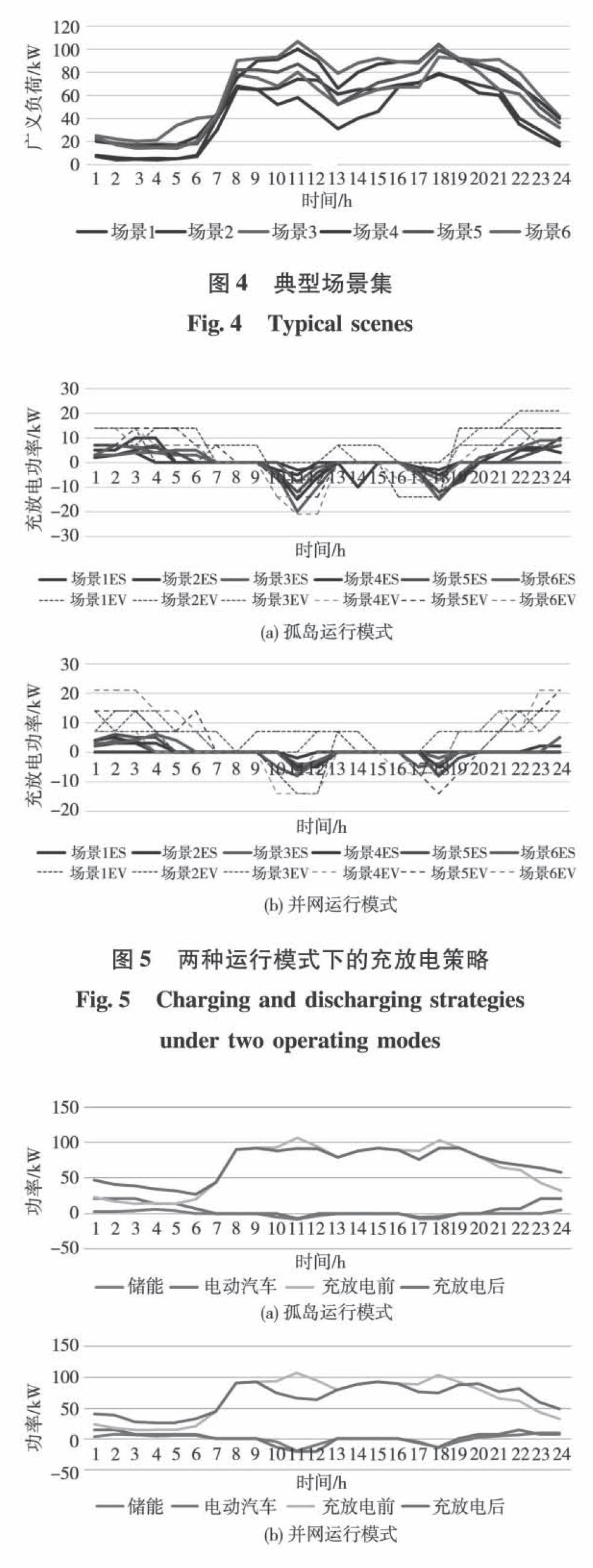
聚類所得的典型場景集如圖4所示，每個場景對應的概率如表4所示。幾個典型場景下儲能和電動汽車在兩種運行狀態下的充放電情況如圖5所示。

通過計算得，并網狀態下，每年所需的購電量為76772.28kwh，購電成本為53085.62元，由圖5的運行曲線可知，該充電策略使儲能與電動汽車在峰荷期放電，在谷荷期充電，用電價低谷期增加的購電量去填補電價高峰期減少的購電量4223.05kwh，購電成本減少了2787.21元，使原購電成本減少5.25%;

在廣義負荷功率水平較低的情況下，如場景l，并網狀態下儲能裝置充放電次數較少，每天的充放電量僅4kwh，比孤島狀態下減少了16kwh，由此可見該模型方法通過減少儲能的動作次數，延長儲能設備的使用壽命，每年可減少充放電量4025.95kwh，減少設備運維成本1646.61元，使原運維成本減少了43.44%;

以場景6為例，做出充放電前后運行曲線的對比圖，由圖6可知該充放電策略可以削峰填谷，有平滑負荷曲線的作用，使得微型燃氣輪機出力趨于平穩，既延長了微型燃氣輪機機組的壽命，又保證了微電網的安全穩定運行。

5 結語

本文引入廣義負荷作為研究對象，充分考慮了新能源出力與負荷的時序相關性。建立了并網與孤島兩種運行狀態下的數學模型，并用改進的粒子群算法求解。算例表明本文所提的優化方法可以有效平緩負荷曲線的波動，減少儲能設備的充放電頻數。并網運行模式下，增加儲能與電動汽車在電網低谷電價時段的充電量和在電網高峰電價時段的放電量，帶來一定的經濟效益;孤島運行模式下，在不滿足電力平衡約束或爬坡約束的情況下切除部分次要負荷，維持微電網安全穩定運行。