單元重構：凸顯知識聯系

陳云

摘要：數學知識的教學，教師應引導學生在分析、比較中厘清相關知識之間的區別和聯系，理解知識的本質，從數學最本真的意義上去感受知識的整體架構。對蘇教版小學數學二年級上冊《表內除法（一）》單元內容進行分析，重構為《認識平均分》《認識除法》《用口訣求商》3個課時，并給出相應的教學設計，以凸顯知識之間的聯系。

關鍵詞：小學數學單元重構知識聯系表內除法

數學知識的教學，教師應引導學生在分析、比較中厘清相關知識之間的區別和聯系，理解知識的本質，從數學最本真的意義上去感受知識的整體架構。教學蘇教版小學數學二年級上冊《表內除法（一）》單元，筆者嘗試對單元內容進行分析、重構，并給出相應的課時教學設計，以凸顯知識之間的聯系。

一、單元內容分析

除法作為乘法的逆運算，其意義建構必然要建立在乘法的基礎上，且運算操作也必須運用乘法口訣，這決定了除法的學習要和乘法一以貫之。因此，蘇教版小學數學教材將《表內除法（一）》安排在二年級上冊第四單元，緊接第三單元《表內乘法（一）》。

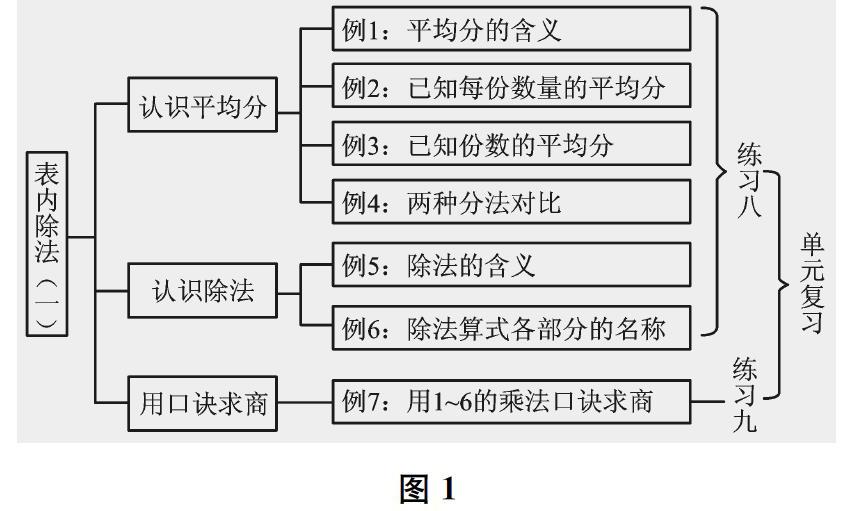
本單元的內容可以分為三個板塊：認識平均分、認識除法和用口訣求商。具體安排如圖1所示。

從中可以看到，教材在“認識平均分”板塊安排了比較多的內容（4道例題），并且非常注重學生的動手操作（把兩種平均分的情形在開放的操作和思考中進行比較），以幫助學生對“平均分”的概念形成具體的表象支撐，從而為除法的認識奠定基礎。緊接著，教材通過例5和例6，分別闡釋了“平均除”和“包含除”兩種情形，旨在幫助學生逐步學會用除法算式表示平均分。這樣的安排能分散難點，助力學生學會一定程度的抽象和概括。

但我們同時也會遇到這樣一些“疙瘩”：

1.“認識平均分”和“認識除法”兩個板塊都把“平均除”和“包含除”分到了不同課時進行教學（例2是已知每份數量的平均分，例3是已知份數的平均分;例5是“平均除”，例6是“包含除”）。這樣雖然有利于學生逐一突破對不同形式的“除法”的理解，固化某一種分法的過程及結果，但同時也可能會打散知識間的聯系，不利于學生統整知識點。

2.在乘法的學習中，教材通過具體情境來幫助學生理解乘法是“求相同加數的和的簡便計算”，很好地解釋了乘法產生的必要性;而在除法的學習中，教材卻把對“平均分的過程就是連續減幾個相同減數的問題”的理解放到了“用口訣求商”板塊（如圖2），這樣的編排相對滯后，也顯得突兀，沒有很好地解釋除法算式產生的過程及其必要性。

3.除法是乘法的逆運算，除法的產生和計算都與乘法有著密不可分的關系，但教材并沒有在例題中安排相關內容的專題突破，只在練習中安排了除法算式與乘法算式的比較;同時，作為除法的初步認識單元，理解除法的含義和用口訣求商既是本單元教學的重點，又是教學的難點，但教材對這些內容的突破也稍顯用力不夠。

二、單元內容重構

（一）基于學情，精簡課時

二年級學生在經歷了一年多的數學學習后，已經有了用“分與合”的方法解決問題的經驗，也具備“怎樣分就公平”的豐富的生活經驗;其思維處于由具體形象思維向抽象邏輯思維發展的過渡階段，具備一定的遷移能力。因此，學生理解“平均分”的難度并不大，教學應重在讓他們經歷和比較兩種“平均分”的過程，緊接著兩種平均分的比較之后，可以出現除法的兩種形式，而在“平均除”和“包含除”比較的同時，可以增加除法與乘法的比較，最后可以結合除法與乘法的關系引出“用口訣求商”。這樣，雖然增加了除法與乘法比較的相關內容，但新授課時反而可以由5課時精簡為3課時。

（二）單元整合，重組內容

由5課時改為3課時，教學內容就要重組：（1）把“用口訣求商”板塊中“除法與減法的聯系”移到第一課時，引導學生用連減的方法記錄平均分的過程;（2）“平均除”和“包含除”對應“已知份數的平均分”和“已知每份數量的平均分”兩種分法，可以一邊比較兩種平均分過程與意義上的異同，一邊引入不同形式的兩種除法;（3）引入“把一些相同數量合起來”和“把一個總數分成一些相同數量”的分與合的實際問題，通過除法與乘法的比較，使學生感受除法各部分的意義及名稱，并通過除法算式與乘法算式各部分之間的聯系自主找到“求商”的方法。

（三）把握重點，凸顯聯系

重組后的3課時，分別對應不同的教學重點。

第一課時《認識平均分》的重點：經歷“已知份數”和“已知每份的數量”兩種平均分的過程，嘗試用減法記錄平均分的過程，為除法的教學奠定基礎。

第二課時《認識除法》的重點：經歷從“平均分”的過程中抽象出除法算式的過程，發現和總結不同的分法列出的除法算式意義上的聯系與區別。

第三課時《用口訣求商》的重點：從除法與乘法的比較中發現兩者的聯系，找到除法算式與乘法算式各部分之間的關系，理解除法運算為什么可以用乘法口訣，并找出一句口訣能解決哪些數學問題。

三、單元教學設計

（一）第一課時《認識平均分》

1.情境引入，發現平均分。

出示問題情境：美工小組正在做紙鶴，王老師把準備好的彩紙平均分給了4位同學，每位同學拿到了3張，你知道王老師準備了多少張彩紙嗎？

指名一位學生列式并說一說為什么用乘法計算。

導入：生活中大量存在著像這樣要把一些相同數量合成一個總數的問題。

改變問題情境：這時候，又來了兩位同學，王老師要重新分配這些彩紙，你覺得要怎么分？

預設：每人分得同樣多才是公平的。

小結：每人分得同樣多在數學上叫作平均分;生活中也大量存在著像這樣要把一個總數分成每份同樣多的問題。

[設計意圖：從乘法問題引入平均分，讓學生初步感知除法與乘法的互逆關系，幫助學生從“合”與“分”的角度去理解乘法與除法的聯系。這樣的設計貼近學生的“最近發展區”，能有效調動學生學習的內在需求。]

2.聯系生活，解讀平均分。

提問：你認為怎樣就是平均分？

學生根據自己的理解交流，并最終得出：平均分就是每份同樣多。

學習活動1：聯系生活，說一個平均分的故事。

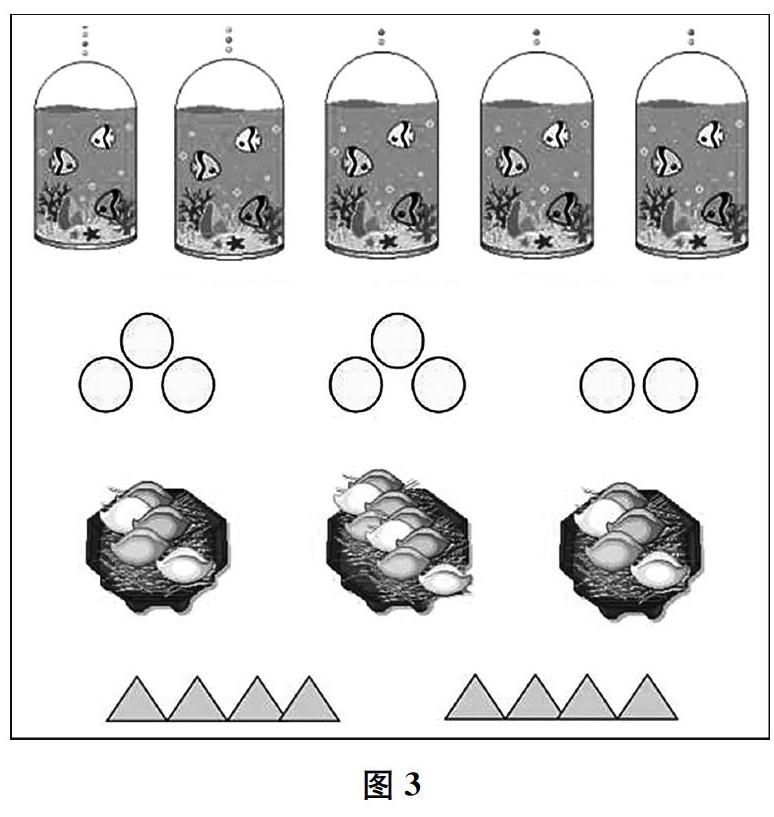
學習活動2：圖3中的幾種情況是不是平均分？為什么？

[設計意圖：引導學生聯系已有的生活經驗和已學的知識說一說平均分，并結合具體的事例初步建立平均分的表象。]

3.解決問題，經歷平均分。

（1）已知每份數量的平均分。

出示問題：這個（不透明）袋子里有一些彩珠，老師想給每位同學兩顆，能分給幾位同學呢？

先讓學生猜測，然后點出：胡亂猜測沒有意義，可以實際分一分。

指名一位學生上臺操作分的過程：先拿出兩顆遞給第一位同學。

提示：現在老師袋子中的彩珠發生了什么變化？（少了兩顆）怎么記錄這個過程？

引導用符號（如“？”）代替袋子中未知的數量，拿走兩顆就是減去2。

學生繼續操作并記錄，最終得到：？-2-2-2=0。

引導小結：①總數是6;②6里面有3個2;③已知每份數量的平均分的過程可以表示成連減的算式。

（2）已知份數的平均分。

出示問題：老師這里還有一個袋子，里面也有一些彩珠，我想把它們平均分給3位同學，每位同學能分到幾顆彩珠？

組織學生交流分法，并請一位學生上臺操作。

結合學生操作，逐級追問：為什么不像剛才那樣，把每人應得到的彩珠直接分給他？當每人分得一顆彩珠時，袋子中的彩珠總數發生了怎樣的變化？

引導交流、總結：因為不知道每人能分到幾顆，所以要逐次分;為了保證每人最終分到的數量同樣多，可以一次給每人分一顆，如果還有剩余，再接著分。

再請一位學生上臺分一分，其他學生記錄分的過程：？-3-3-3-3=0。

引導小結：①總數是12;②12平均分成3份，每份是4;③已知份數的平均分的過程也可以表示成連減的算式。

（3）“動手做”。

提問：用18個相同的小正方形拼成不同的長方形，你想怎么分？

引導分兩種情況思考：①先確定要分的行數，再實際分一分，看每行能分幾個;②先確定每行的數量，再試一試可以分成幾行。

[設計意圖：在開放的活動中，學生通過對比感受到，雖然兩種分法分的過程有區別，但其本質還是有內在聯系的。用減法記錄分的過程，建立起減法和除法之間的聯系，為除法的產生做鋪墊。“動手做”環節，用18個小正方形拼長方形，是對兩種平均分過程的再比較，同時也是對除法與乘法聯系的再感知。]

（二）第二課時《認識除法》

1.結合平均分，引出除法。

出示問題：24只氣球，每4只扎一束，可以扎成幾束？

引導列出算式（24-4-4-4-4-4-4=0），得出：24里面有6個4，所以可以扎成6束。

追問：這是一個什么問題？減法表示什么？如果這里有48只氣球呢？96只氣球呢？

引導發現：隨著數字增大，用減法來解決太麻煩了。

引發思考：在前面的學習中，我們知道，一些相同加數相加時，為了簡便，可以列乘法算式，那么想想看，這里連續減一個相同的減數，會不會有什么簡便的方法呢？

引入除法：像這樣平均分的問題在數學上可以用除法來計算，把24只氣球平均分，每份4只，就可以寫成24÷4;剛剛我們已經知道可以分給6個人，所以就等于6。

介紹除號的寫法和讀法，以及表示的意義（平均分）。

[設計意圖：引入較大數平均分的問題，讓學生感受用連減的方法來解決很麻煩;再結合乘法是“求相同加數的和的簡便計算”這一已有認知，遷移猜想連續減一個相同減數，一定也有相應的簡便計算，順理成章地引入除法。]

2.認識除法，解讀算式的意義。

結合分氣球情境，指名學生說一說“24÷4=6”中每個數字表示的含義。

提問：回顧上節課“分彩珠”的過程，6顆彩珠，每人分兩顆，可以分給幾位同學？這個問題你能用除法算式來表示嗎？并說一說這道算式表示的意義。

置換問題情境：24只氣球，平均扎成4束，每束有幾只？這個問題可以列成除法算式嗎？為什么？請你列出算式，并說一說算式的每一部分分別表示什么。

引導用同樣的方法解決上節課其他“分彩珠”問題。

[設計意圖：通過相同情境中的兩種不同分法，引導學生了解除號和除法算式所表達的意義，并用除法解決上節課中的平均分問題，進一步感受用除法解決平均分問題的便捷。]

3.比較除法，認識各部分的名稱。

同屏出示兩道除法問題和算式，引導觀察比較：這兩個問題有什么相同點和不同點？

引導小組交流、全班匯報。相同點：都是表示平均分的問題，所以都是用除法解決;都是已知總數（教師結合學生的匯報介紹：這個總數在除法中就是被除數，也就是這個總數被平均分了）。不同點：一題是已知每份的數量，另一題是已知份數（教師結合學生匯報介紹：這個已知的量不管是每份的數量還是份數，在除法中就是那個被連續減的減數，叫作除數）;最后求出來的結果表示的意義也不同（教師介紹：這個最終結果的意義不同，但都叫作商）。

請學生獨立完成課本“反饋習題”，并指出被除數、除數和商分別在哪里，表示什么意思。

提問：除法中這個總數叫“被除數”，減法中的總數叫“被減數”，都有一個“被”字，你能說說你是怎么理解的嗎？

引導發現：“被除數”和“被減數”都是總數，都是被分的對象;減法可能不是平均分，除法一定要是平均分;減法算出的是其中一個部分的數量，除法算出的是所有部分相同的數量或有幾個相同的部分。

[設計意圖：通過對“平均除”和“包含除”兩種除法的對比，引導學生發現其本質意義是相同的，進一步強化對除法的理解。通過“被除數”“被減數”兩個名稱上的相似，引導學生找到除法與減法的聯系與區別，打通知識間的“隱蔽通道”。]

（三）第三課時《用口訣求商》

1.聯系實際，感受除法與乘法的互逆關系。

出示問題情境：學校給每個班分發了一些必讀書籍，王老師把這些書整整齊齊地擺放在書桌上，（1）每堆放4本，5堆一共多少本？（2）一共有20本，每堆放4本，可以放幾堆？（3）一共有20本，平均分成5堆，每堆可以放幾本？

指名學生列式并說一說為什么用乘法或除法計算。

提問：觀察這3個問題，你能說說什么時候用乘法計算，什么時候用除法計算嗎？

引導發現：問題（1）求總數，5個4相加就能得到總數，可以用乘法計算;問題（2）和問題（3）都是已知總數，把這個總數連續減，也就是平均分，可以用除法計算。

[設計意圖：通過同一情境下的除法與乘法問題的比較，感受乘法是求總數，除法是已知總數求份數或每份數量，除法與乘法之間存在互逆關系，為用乘法口訣解決除法問題做鋪墊。]

2.用口訣計算。

提問：乘法你能用乘法口訣計算，那除法呢？不看圖你會計算嗎？你是怎么想的？

預設：（1）從乘法中去找，乘法的積是被除數，一個乘數是除數，另一個乘數就是商;（2）20÷4，其實也就是想4個幾是20，同樣可以用4的乘法口訣計算;（3）實際分一分，就知道商是幾;（4）用20連續減4，看能減幾個4。

引導比較：這幾種算法有什么共同點？哪種方法更簡便？

提問：通過這幾道題的計算，你發現了什么？

引導發現：“四五二十”這句口訣可以用于計算4×5、5×4、20÷5、20÷4四道算式。

反饋練習：（1）看算式想口訣;（2）看口訣寫四道算式。

[設計意圖：引導學生先用乘法口訣解決乘法問題，再思考怎么計算除法算式。在對多種計算方法的比較中發現其實質都是求4個幾是20，歸結到乘法口訣可以解決的問題上來，并通過反饋練習鞏固一句口訣對應的乘法和除法算式。]

3.自主編題。

出示圖4，提問：看圖，你能寫出一道乘法算式和兩道除法算式嗎？

指名學生列式。

引發思考：你要運用哪些數學信息，提出怎樣的問題，才能列出乘法算式？要列出除法算式呢？你又是怎樣計算這些乘法、除法算式的？

[設計意圖：從看問題列算式，到看圖提出用乘法和除法來解決的問題，學生的思維要更加理性——要提出用乘法解決的問題，就不能在信息中涉及總數，而要把求總數放在問題里;要提出用除法解決的問題，就要先表明總數是多少，再平均分，由此可以進一步鞏固除法和平均分模型。]