例談引導學生數學探究的問題類型

孫曉華

摘要：問題驅動甚至決定著學生的探索、發現活動，把探索、發現活動變成解決問題的過程。在數學教學中，教師應該特別注意提出激發探究欲望的啟思問題、反映數學實質的核心問題、突破生成障礙的關鍵問題、指向“綜合與實踐”的應用問題。

關鍵詞：數學探究啟思問題核心問題關鍵問題應用問題

新課標的理念強調，數學教學要以學生為主體，引導學生自主探索、發現，以建構、理解數學知識與方法，鍛煉、發展數學思維與能力。因此，教師要提供適當的“誘因”，引導學生的探索、發現活動。

“學起于思，思源于疑。”問題便是最重要的“誘因”。問題驅動甚至決定著學生的探索、發現活動，把探索、發現活動變成解決問題的過程。那么，在數學教學中，教師應該提出怎樣的問題呢？筆者認為，以下幾類問題必不可少。

一、激發探究欲望的啟思問題

這類啟思問題，重在激發學生的探究欲望，為接下來的探究活動做好情緒鋪墊，并提供方向和線索。驚奇是學生探究的強勁動力。所以，教師設計啟思問題時，要通過一些看起來很神奇的情境和現象給學生強烈的刺激，讓學生產生認知沖突，感到疑惑不解，從而急切地想探索問題背后的原因和本質，解答自己的疑惑。

例如，教學《和與積的奇偶性》一課時，為了引出探究“和的奇偶性規律”的需求，可以這樣創設啟思問題——

師見證奇跡的時刻就要來臨了！請第一組學號是奇數的同學起立。

（5名學生起立。）

師（停頓片刻）哦，那我知道了，如果把他們的學號表示的數相加，和應該是奇數。你們信嗎？

（學生半信半疑。然后，站著的學生報學號，其他學生用計算器計算它們的和，發現確實是奇數。）

師說不定是蒙對的呢！再來一次怎么樣？索性增加點難度：你們來挑一個組，請學號是奇數同學的起立。

（學生選擇第三組，8名學生起立。）

師（環顧片刻）把這一組站起來的同學的學號表示的數相加，和應該是偶數。

（學生迫不及待地報學號，用計算器計算它們的和，發現確實是偶數。）

師老師甚至都不用知道同學們的學號，就判斷出了和是奇數還是偶數。這里是不是藏著什么秘密呀？

這時，學生的驚奇感一下子被激發出來了，他們迫切地想知道和是奇數還是偶數會與什么有關，會是什么原因，于是，接下去的探究會帶有強烈的動機。

二、反映數學實質的核心問題

核心問題是經過精心提煉的反映教學主題（即數學實質）的問題，通常是關于“是什么”“有哪些要素”“為什么”“從哪里來”“有什么用”“怎么辦”“有什么步驟”等的根本問題，指引著理解知識本質、追溯問題本源等基本方向。這類問題往往直接指向教學目標，處于數學探究的核心。

例如，教學《百分數的意義》一課之前，學生對百分數已經有了一定的認識：在生活中見過了，甚至會讀、會寫了。那么，關于百分數，學生還要學習什么呢？教師可以向學生提出這個問題。憑借已有經驗，學生會以問題的形式提出各種想知道（探究）的內容。這時，教師便可以從學生的問題中精選、提煉出三個核心問題：（1）什么叫百分數？（2）百分數有什么用？（3）百分數和分數有什么聯系和區別？由此引導學生展開本節課的探究學習。這三個問題的解決便意味著本節課教學目標的達成。

確定核心問題時，除了要注意教學目標之外，還要注意學生的學習起點以及學生的學習可能。

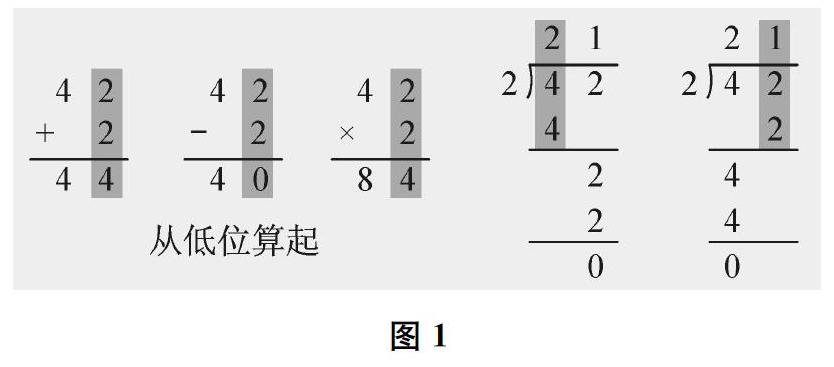
例如，教學《兩位數除以一位數（首位不能整除）》一課之前，學生由于有“兩位數除以一位數（首位能整除）”的計算經驗，已經會模仿著計算了。所以，“怎樣算”不再是學生學習的起點問題，“為什么這樣算”才是他們亟待解決的。因此，教師可以出示圖1，從學生的立場提出問題：在計算加法、減法、乘法的時候，我們都是從個位算起的，為什么到了除法，卻要從高位除起呢？

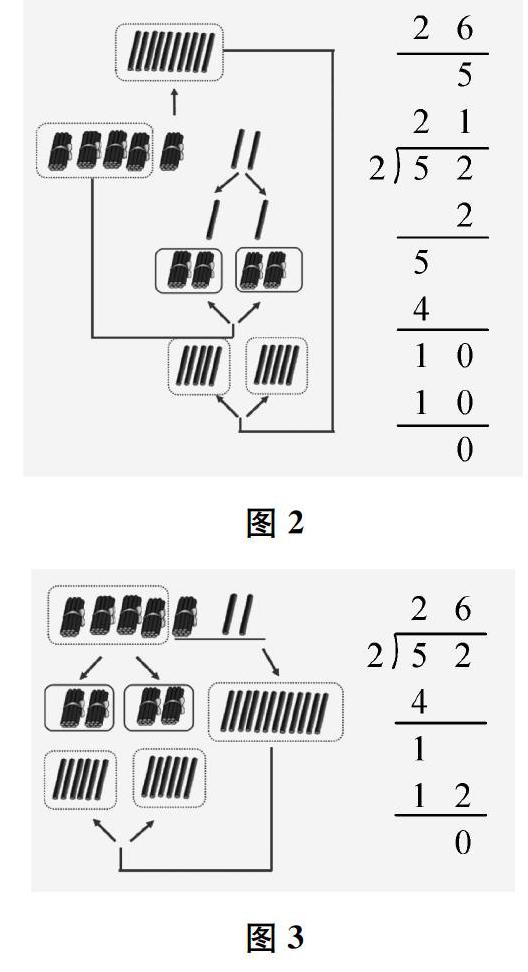
根據原有經驗，學生會發現，首位能整除的情況完全可以從個位除起：42除以2，先用個位上的2除以2，商1，再用十位上的4除以2，商2，結果是21。學生感到困惑，于是轉向首位不能整除的情況。分小棒和豎式的一一對應，讓學生恍然大悟：如圖2，從低位算起就是先分單根，再分整捆，這樣太麻煩了;如圖3，從高位算起就是先分整捆，再分單根，這樣簡捷很多。通過逐層解析，法理相融，計算教學清晰明了。

三、突破生成障礙的關鍵問題

顧名思義，這樣的關鍵問題是幫助學生突破學習過程中生成的障礙的問題，通常需要以巧妙的設計，來指引學生思維的轉換。它往往指向教學重難點，處于數學探究的關鍵。

例如，探究“和的奇偶性規律”時，學生在找到兩個數和的奇偶性規律后，探索多個數和的奇偶性規律時，一度陷入了迷茫。這時，教師提問：400+28，和是偶數，再加上26，和是奇數還是偶數？再加162呢？如果加的是5呢？學生回答后，教師出示下頁圖4，進行追問：加數中什么樣的數可能改變和的奇偶性？學生回答“奇數”。教師出示圖5，繼續追問：再來一組，33+127，和是偶數，再加一個什么數，和就變成了奇數？學生還是回答“奇數”。以上設計巧妙的連續問題，引導學生把關注點落到了加數中的奇數身上，相當于在學生探究的道路上遞出了一根拐杖，牽引著學生逼近和的奇偶性規律的真相。

四、指向“綜合與實踐”的應用問題

“學以致用”是學習的高級階段，它不僅能夠激發學生學習數學的興趣，讓學生體會到數學的價值，而且能夠鞏固和促進學生的數學理解。應用問題主要是與現實生活或其他學科有關的情境問題。教師可以通過應用問題，設計項目化的“綜合與實踐”活動，引導學生深度學習，發展高階思維。

例如，從“汽車超速了嗎？”這個問題，引出測速儀的功能，繼而產生新的問題：測速儀是如何測速的？于是，讓學生探尋測速的原理，最終指向研究數學中的速度、時間、路程之間的關系。

再如，“怎樣測量比較高的物體（如大樓、旗桿、大樹等）的高度？”這個問題，可以調用關于比例的知識，找到相應的數學模型：以同樣的焦距拍照，那么，照片中大樓的高度、實際的大樓的高度與照片中門的高度、實際的門的高度具有同樣的倍比關系。這樣一來，測量照片中大樓的高度、照片中門的高度、實際的門的高度，就可運用比例的知識推算出實際的大樓的高度了。