初中數學習題變式思維能力訓練分析

王鋒

【摘要】初中數學習題變式思維能力的訓練，不單單要是基礎知識、基本技能、思維的訓練，還能有效地實現新課程三維教學目標，提高學生解題能力，還能促進學生數學核心素養的形成。

【關鍵詞】初中數學 ?習題變式 ?思維能力訓練

【中圖分類號】G633.6 ?【文獻標識碼】A 【文章編號】2095-3089（2020）17-0120-01

數學教學中，變式教學本質就是說通過不同角度、不同的側面、不同的背景，從多個方面變更所提供的數學對象或數學問題的呈現形式，使事物的非本質特征發生變化而本質特征保持不變的教學形式。因此，能夠培養學生數學的思變思維，促進學生解題能力的提升，進而形成一定數學核心素養。一般來說，題目變式有這些方向，那就是條件的弱化或強化;結論的延伸與拓展;圖形的變式與延伸;條件與結論的互換;基本圖形的構造應用，多個方面的綜合，教師可以從這些方面著手，組織適當的習題變式思維能力訓練活動。

一、綜合多種知識進行變式，向學生滲透習題變式思維

在對例習題教學功能的挖掘方面，教師應當學會綜合使用多種變式方法，通過習題演變的策略，滲透給學生習題變式思維，引起學生對于習題變式的重視。下面這兩道訓練題綜合了圖形知識、函數知識、平移知識、比例知識，是非常典型的綜合變式，在培養學生變式思維上有著積極作用。

例如，題型1：有一副直角三角板，在三角板ABC中，BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4，將這副直角三角板按如圖1所示位置擺放，點B與點F重合，直角邊BA與FD在同一條直線上，現固定三角板ABC，將三角板DEF沿射線BA方向平行移動，當點F運動到點A時停止運動。

（1）如圖2，當三角板DEF運動到點D到點A重合時，設EF與BC交于點M，∠EMC=？

（2）如圖3，當三角板DEF運動過程中，當EF經過點C時，求FC的長。

（3）在三角板DEF運動過程中，設BF=x，兩塊三角板重合部分的面積為y，求y與x的函數解析式，并求出對應的x取值范圍。

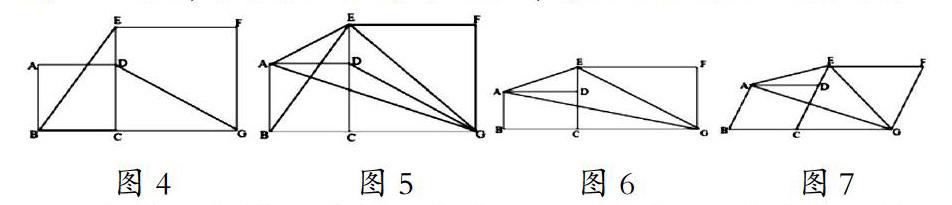
如圖4，正方形ABCD的邊CD在正方形CEFG的邊CE上，連接BE、DG，BE，DG的數量關系和位置關系分別是？

變式1：如圖5，連接AG、AE、EG，若正方形ABCD的面積是4，正方形ECGF的面積是9，則△AEG的面積是多少？

變式2：如圖6，矩形ABCD的邊CD在矩形CEFG的邊CE上，且AB/BC=CE/CG，連接AG、AE、EG，若矩形ABCD的面積是4，矩形ECGF的面積是9，則△AEG的面積是多少？

變式3：如圖7，平行四邊形ABCD的邊CD在平行四邊形CEFG的邊CE上，且AB/BC=CE/CG，連接AG、AE、EG，若平行四邊形ABCD的面積是4，平行四邊形ECGF的面積是9，則△AEG的面積是多少？

二、鍛煉學生的思維變式，不斷挖掘學生的潛力

思維變式往往指的是以上幾種變式的綜合，尤其是題目變式，“多題一解”與方法變式，也就是“一題多解”，在數學教學過程中，利用此類變式問題，可培養學生思維的靈活性、深刻性和發散性，使學生舉一反三、融會貫通，從而更好地挖掘學生的潛能，提高學生的綜合素質。

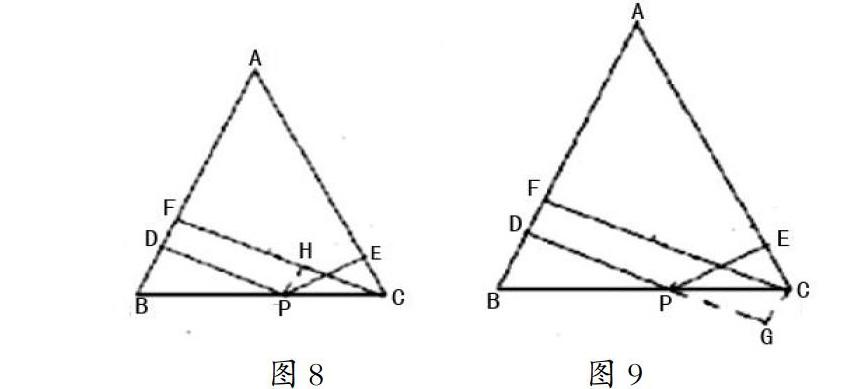
例，如圖8，在△ABC中，AB=AC，P為BC上的動點，過點P作PD⊥AB，PE⊥AC垂足分別為D，E;CF為AB邊上的高線。求證：PD+PE=CF。此題的證明方法就很多種。

證法1是截長法：過點P作PH⊥FC于點H，容易證明四邊形DPHF是矩形。∴PD=FH，也容易證得△PEC≌Rt△CHP，∴PE=CH，∴PD+PE=FH+CH=CF。輔助線見圖8。

證法2是補短法，過點C作CG⊥DP，交DP的延長線于點G，容易證得四邊形DGCF是矩形。∴FC=DG=PD+PG;∴CG∥AB;∴∠PCG=∠B=∠ACP;∴Rt△PGC≌Rt△PEC;∴PG=PE;∴FC=PD+PE。輔助線見圖9。

三、變式數量要在合適范圍，符合初中生認知水平

習題變式的訓練中，教師要控制變式數量，保證在合理的范圍內，以符合初中生的認知水平，才能更好地訓練學生的變式思維，提高解題能力。可以嘗試在原題的條件下，挖掘所求的結論，也可以在改變原題條件之下，充分挖掘所求結論。

例，如圖10，一塊鐵皮呈銳角三角形，它的邊BC=80cm，高AD=60cm，要把它加工成矩形零件，使矩形的長、寬之比為2：1，并且矩形長的一邊位于BC上，另兩個頂點分別在邊AB、AC上求這個矩形零件的長與寬，這是原題。對其中一些條件進行改變，出現了變式題，一塊鐵皮呈三角形，∠BAC=90°，要把它加工成矩形零件，使矩形一邊位于BC上，另兩個頂點分別在邊AB、AC上。試問：PS、BS、CR之間有何關系？為什么？這樣的變式沒有超出學生能力，培養學生變式思維的同時，提高了學生的自信心，有助于更多變式習題訓練的開展。

結束語

綜上所述，變式教學是中國基礎教育中的精華，是一種十分重要的教學思想，是經實踐證明的有效教學模式，值得教師們進行實踐。所以，初中教學中教師要遵循變式教學規律，合理組織變式習題訓練，促使學生數學思維的形成，不斷提高解題能力。

參考文獻：

[1]萬煉城.農村初中數學變式教學在習題課的案例研究[J].數學學習與研究，2019（04）：124.