注重運算教學 提升思維品質

楊紅干

[摘 要]? 運算教學既要讓學生在直觀中理解算理，也要讓學生明白抽象的法則，更需要讓學生充分體驗由算理直觀化到算法抽象化間的過渡和演變，從而達到對算理的深層理解和對算法的切實把握，提升學生的思維品質。

[關鍵詞] 小學數學;運算教學;思維品質

《數學課程標準（2011年版）》中明確指出：“運算能力主要是指能夠根據法則和運算律正確地進行運算的能力。培養運算能力有助于學生理解運算的算理，尋求合理簡潔的運算途徑解決問題。”從中我們不難看出，運算能力不但要會算、算正確，還包括對算理的理解從而解決問題。從運算內容來看，運算能力包含數的運算能力和符號運算能力，在小學階段主要是針對前者的培養，具體而言主要體現在：計數能力的形成、運算法則和公式的掌握、應用問題的解答三個方面。從運算過程來看，運算能力包括運算過程中學生呈現的思維能力，也包括在實施運算過程中遇到問題而調整運算的能力。所以運算能力是每個公民必須具備的基本素養之一。

一、“小題大做”——梳理運算錯因，拓展學生思維

教學中我們不難發現，許多高年級的學生，在計算上仍會犯“6×9=45”“24×5=100”“8×9÷8×9=1”這樣的低級錯誤，而且這樣的錯誤不斷重犯難以更改。究其原因，是學生做錯時或許僅僅只是把答案改正確，或自認為“粗心”所致。而沒有從根本上找出病因，鉆進下次遇到還會做錯的怪圈。因此我們需要發現學生存在的共性問題，而不能簡單地讓學生“一改了之”，需將一道錯題“放大”，引導學生發現問題、分析問題、解決問題、反思問題。

案例1：蘇教版義務教育教科書三年級上冊“兩位數乘一位數的口算”

師：剛剛那位同學說24×5=100，你們同意嗎？

生：我們算出的結果是120，所以24×5=100是錯的。

師：誰能猜一猜結果是100的同學是怎么想的？

生：他可能把24×5看成是25×4了，25的好朋友是4，因為25×4=100，所以我猜測他看到24×5或25×4都會寫成100，我也曾經發生過這種錯誤。

師：你既會總結也會反思！像這樣容易看錯的算式在平時的學習中還有很多，你們能試著舉幾個例子嗎？（學生找出14×5和15×4、17×4與14×7……）

師：通過舉例你能發現他們錯誤的原因嗎？或在以后的計算中有哪些需要提醒同伴的？

華應龍老師說：錯若化開，成長自來。特別是在計算教學中，常常出現各種各樣的錯誤。課堂教學中，我們應引導學生自己去尋找錯誤的根源，使學生在探究中真正掌握和理解所學知識，獲取不同的發展。本案例的本質以“24×5得多少？”，引導學生發現并改正計算中的錯誤，同時借助問題鏈將學生計算習慣、思維潛意識中的問題暴露出來，從而從個例現象上升到共性問題，并引導學生從思維源頭上找到錯誤的原因，避免此類錯誤的再發生。本來一個很簡單的錯題更正，在教師的引領和不斷追問中，實現了由點到面、由小見大、由外在形式到思維本質上的提升。可見，當學生出現錯誤時，適度“放大錯誤”，錯若化開，精彩自來！同時有利于拓展學生的思維，提升學生的思維品質，促進學生多元化的思考。

二、“融理入法”——建構運算體系，促進數學理解

讓枯燥的運算教學變得有意思，這就需要我們在運算教學中促進學生的“數學理解”來激發他們的運算興趣。此時可以借助直觀——溝通直觀和抽象的聯系，形成直觀模型;也可以借助生活經驗——創設情境啟發學生思考;還可以借助講故事——有趣的表達可以加深學生對數學的獨特理解。當然為了處理好算法直觀和算理抽象的關系，我們要引導學生理解算理時運用學具操作、圖片對照等直觀的手段，比較清晰地揭示算理;同時要充分運用學生生成的資源，引導學生進一步抽象，觀察外在形式不一樣的背后其本質是一樣的，還需引導學生通過觀察、比較，尋找它們共同點，實則是算理抽象的過程，是學生抽象思維發展的過程，也是發展學生思維力不可缺失的一部分。

案例2：蘇教版義務教育教科書三年級下冊《兩位數乘兩位數的筆算》

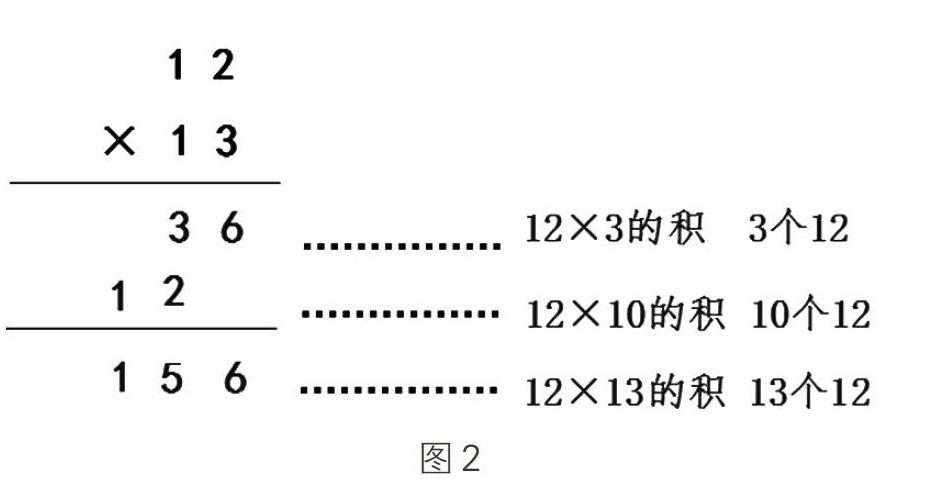
當教師呈現12×13時，學生試做后展示學生算法的多樣化，選擇列乘法豎式的學生接受大家的提問。

生：為什么第一個6的下面是空著的？

生：因為這個地方有個隱形的0省略啦，它表示120。120表示12×10。

生：36表示什么意思？156呢？

生：36表示12×3;156表示12×3+12×10的和。

生：為什么乘法算式，最后是加法運算呢？

生：我們可以把12×13看成一個大口袋，里面裝著13個12，后來我們把它分成了兩個小口袋，一個袋里裝著3個12，另一個口袋里裝著10個12，最后把它們合起來就用加法啊。

師：12×13這樣的算式在生活中見過嗎？

生：購物時用到，比如：一個玩具12元，我買了13個玩具，請問我應該付多少錢？

生：學校的同學排隊做操，如果每排站12人，共有13排，求一共有多少人？

師：如果結合黑板上大家剛剛在生活中找的那些事，算式就會說話啦，我們就以：一個玩具12元，買13個玩具多少元為例，誰來說一說？

生：12×3就表示買3個玩具的價錢。12×10自然就表示買10個玩具的價錢。把3個玩具的錢和10個玩具的錢合起來就是13個玩具的錢。

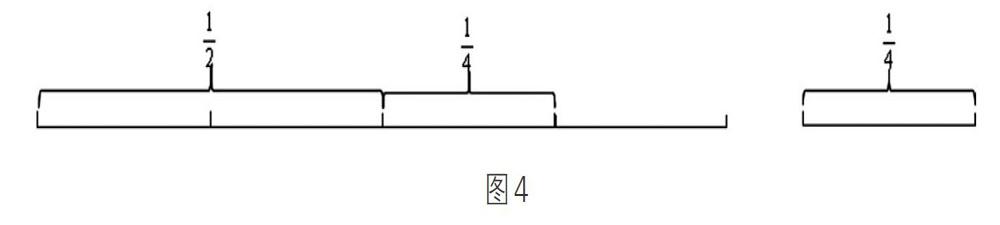
生：我畫圖了（如圖3），結合圖看剛剛大家的想法就一目了然了。

心理學研究表明小學生思維發展規律是直觀動作思維——具體形象思維——抽象邏輯思維，因此學生在自主探索算法時，我們需深入到學生中去，掌握不同學生的算法，在交流匯報時可以有意識的有層次的匯報，處理好算法多樣和算法優化的關系。學生借助圖式把兩位數乘兩位數的算理用直觀的形式外顯出來，當然這種圖式一定要勾——勾聯系、勾關聯。如此方可以有效地幫助學生理清算理、感知算理、內化算理，培養學生的運算能力。

三、“單位累加”——滲透運算單位，掌握核心概念

學生計算能力的培養，應該讓學生在有效的活動中，明晰核心問題，分析運算過程，在運算程序中感悟到算理，滲透數學思想方法，從而培養學生的思維能力，促進數學素養的養成。我們說數是“數”出來的，那么“數”的是什么呢？“數”的是計數單位。認識數位、計數單位是數的意義和運算教學的核心目標，而運算教學的一個核心概念就是計數單位。數的加減法運算是相同計數單位的累加;數的乘法是相同數的和的運算;數的除法在某一位上，除什么呢？就是分單位的個數;當單位的個數不夠分時怎么辦？再把單位細分繼續分。

學生的素養不是“教”出來的，是學生“悟”出來的，傳統教學只重視計數單位的知識講授，使得學生對計數單位的學習只停留在數的組成和分解之中，沒有經歷計數單位從量變到質變的逐步累加。無論整數、分數、小數它們都是通過單位累加得到不同的數，當然整數的十進制是學生學習時間最長，生活體驗最為豐富的內容，抓住計數單位的改變這一主線，先拓展計數單位再帶領學生數計數單位的個數，最大限度地借助整數學習中的經驗，依靠計數單位——學生心中的那把“尺子”，讓學生對小學階段各個數系的認識和運算實現無縫對接。

四、魔術故事——掌握運算規律，激發學生興趣

有趣的故事，毋庸置疑可以很好地幫助兒童理解運算的道理。神奇的魔術同樣也可以為我們的運算課堂教學增添不一樣的色彩，傳說中的那副混亂的撲克牌可以產生許多有趣的運算，而這種運算不是枯燥單一的，它一定是你通過觀察、發現、推理得出算式，從而通過運算的途徑來解決問題。

如臺灣何鳳珠老師用4個不同的小方塊（每個面上寫有不同的數字）摞起來，它可以做什么呢？可以說大小、說關系、算24點、說數的性質。它還可以做什么呢？可以讀數、算數，如通過口算神奇知道2378+9667+5492+7953=25490，6881+3458+6128+6989=23456等的結果，激發學生的興趣和探究的好奇心，學生通過計算驗證結果，師追問從中你們發現了什么？學生通過探究合作發現要尋求個位檔相加等于18，如第一道算式個位檔8，7，3，剩下最為關鍵的第三個數5492，549成為和的中間的三個數，和的個位是8+2的個位即為0，最高位是2，第二道算式是變換關鍵數。

再如吳如浩老師的超級大魔“數”也會很好地激發學生的好奇心，成為運算教學的一大亮點。一次次的數學魔術研修告訴我：心中有學生的數學魔術設計，會讓學生感覺自己來上一堂思考課，而不只是來看一場魔術表演。對于很難讓學生理解的乘法分配律的教學，我先用撲克牌來變個“聽牌術”，即通過任意洗牌然后指出其中一張牌的花色、數字，來激發學生的好奇心，以游戲之心做數學之事！然后通過講故事演情景劇的形式，展開乘法分配率在簡便計算中的教學。

案例4：蘇教版義務教育教科書四年級上冊《乘法分配律》

例如乘法分配律在簡便計算中的運用，以103×16為例，學生經常有以下幾種錯誤的算法：（1）100+3×16，（2）100×3×16，（3）（100+3）×16=100×16+3，我們不難發現（1）、（3）兩種情況是對乘法分配律形的表征有一點的記憶，但對乘法分配律的運算本質不理解。因此在講解乘法分配律的過程中，可以采用講故事的方法來幫助學生理解和掌握。當然故事是外衣，其中蘊含的數學知識才是靈魂。以103×16為例，首先我們選一個數來“動手術”，選誰呢？生都知道選103，它靠近整百數100。把103變為100+3，動完手術后要對它進行“包扎”，否則“病人”會受到感染，所以我們要為100+3添上小括號，前提是結果相等的式子才能變換（如第2個算式是不相等的），于是得到103×16=（100+3）×16，現在“病人”103動了手術要住院療養一段時間，吃點水果——香蕉補補營養吧，此時你腦子得有“香蕉”的畫面感，于是把100和16、3和16用弧線連起來，就得到100×16+3×16=1600+48=1648，回頭看一下還可以用幾個幾來驗證，100個16和3個16合起來就是103個16。舉一反三后孩子們對于25×16如何簡便計算，竟然想出了“切西瓜”游戲，原來是把16變為4×4，乘號像一把刀一樣，我想這種學習的過程會讓學生記憶深刻，直擊思維更深處，感受不一樣的運算學習。

總之，運算教學既要讓學生在直觀中理解算理，也要讓學生明白抽象的法則，更需要讓學生充分體驗由算理直觀化到算法抽象化間的過渡和演變，從而達到對算理的深層理解和對算法的切實把握。特級教師曹培英老師認為：“運算能力”是運算技能與邏輯思維能力的一種獨特的結合;“運算能力”不是簡單的加減乘除計算，而是觀察能力、記憶能力、理解能力、推理能力、表達能力以及想象能力等有關的由低級到高級的綜合能力。計算能力直接反映學生的數學能力。因此，我們在進行運算教學時，除了要教學相應的運算規則和意義外，還需要培養學生的計算能力和思維品質，進而提高學生發現問題和解決問題的能力。

[參 考 文 獻]

[1]提秀雷.“神算”有秘訣[J].教育研究與評論，2016（4）.

[2]張奠宙.小學數學教材中的大道理[M].上海：上海教育出版社，2017.

[3]范冉.神奇的骰子“透視術”[J].小學數學教師，2019（2）.

[4]張景中.運算的規律[J].教育視界，2019（2）.

（責任編輯：李雪虹）