培養學生類比推理能力

劉鵬飛

類比推理是合情推理的重要形式之一，是引發猜想、發現結論的有效途徑。教師可以在性質、法則、定律以及幾何圖形、數形結合教學、解題方法指導教學的過程中，逐步提高學生的類比推理能力。

一、在性質、法則、定律教學中培養

小學數學中有部分內容的性質、法則、定律是相似的。教學中，教師應注重它們之間的聯系，引導學生用類比推理的方法來學習。

例如，“異分母分數加減法”本質上的知識是“相同數位上的數，才能直接相加減”這一計算法則。學生在學習整數、小數、同分母分數加減法時，已經形成了這種計算認識，積累了這種計算經驗。因此，教學時可以先設計一組整數、小數、同分母分數加減法練習，如：

筆者引導學生歸納出計算過程背后隱含的共同核心要素——相同數位上的數，才能直接相加減。學生受這個計算原理的啟發，就能類比嘗試，將異分母分數轉化成同分母分數，再相加減。歸納出異分母分數加減法的法則后，再次進行新舊知識的對比，凸顯出此類計算的共同點，強化新舊知識之間的本質聯系。

還有許多運算定律之間也有十分密切的聯系，比如，整數加減法運算定律對小數、分數同樣適用，加法結合律、交換律對于乘法也同樣適用。這一系列的類比教學活動，能促進學生對知識的深刻理解，幫助他們構建比較完善的知識結構。

二、在幾何圖形的教學中培養

幾何圖形之間也有許多相似之處，在學習新的幾何圖形時，教師應讓學生將其與已學過的、熟悉的圖形進行比較，猜測新圖形可能具有的性質、結構，建立起新舊圖形間的聯系。幾何圖形結構的類比主要有三種形式：平面圖形間的類比、立體圖形間的類比，平面圖形與立體圖形的類比。

1.平面圖形間的類比。在教學正方形的面積計算公式時，我們可以通過長方形與正方形之間的關系以及長方形的面積計算公式，類比出正方形的面積計算公式：

除此之外，小學數學中的其他平面圖形，如平行四邊形、三角形、梯形、圓的周長等公式，都可以由已有圖形推導出來。教師應梳理它們之間的推導過程，幫助學生建立系統化思維。

2.立體圖形間的類比。教學圓柱的體積公式時，我們可以根據等積變形后長方體與原圓柱體之間的關系以及長方體的體積計算公式，類比推出圓柱的體積計算公式：

此外，小學數學中的其他立體圖形之間的性質和結構也有密切的聯系。比如，長方體的體積公式是通過體積單位直接計量而抽象出來的，正方體的體積公式是根據正方體和長方體的關系類比推導出來的，圓錐的體積公式是利用等底等高的圓錐和圓柱的關系，通過實驗推導出來的。

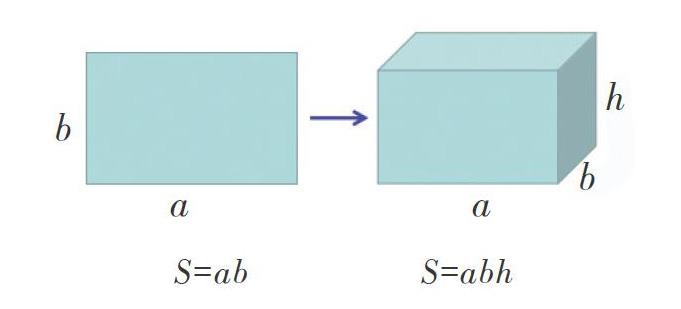
3.平面圖形與立體圖形的類比。平面圖形的邊與立體圖形的面、平面圖形的面積與立體圖形的體積之間以及平面圖形的面積公式推導方法與立體圖形的體積公式推導方法之間都可以進行類比。比如，長方形的面積=長×寬，長方體的體積=長×寬×高：

同時，圓的面積公式的推導方法是將圓平均分成若干等份剪開后拼成近似的長方形，通過長方形面積計算公式推導出來的。圓柱體體積公式的推導方法也是將圓柱的底面平均分成若干等份切開后拼成近似的長方體，根據長方體的體積公式推導出來的。

三、在數形結合教學中培養

數與形是數學研究的兩個對象，借助圖形描述數式，利用數式解釋圖形，這樣的數形類比，能夠啟迪思路，發現規律，培養學生的創造性思維。例如，計算“1+3+5+7+9+11+13=（? ）”時，筆者先讓學生嘗試計算，然后引導學生觀察圖形，發現規律，最后再利用規律，簡便計算（如下圖）。

這樣的解題過程，將數轉換成形，學生受到圖形的啟發，進行數形類比，能夠發現“從1開始，連續奇數相加的和，等于奇數個數的平方”這一數學規律，最后利用發現的規律，簡便地算出得數。

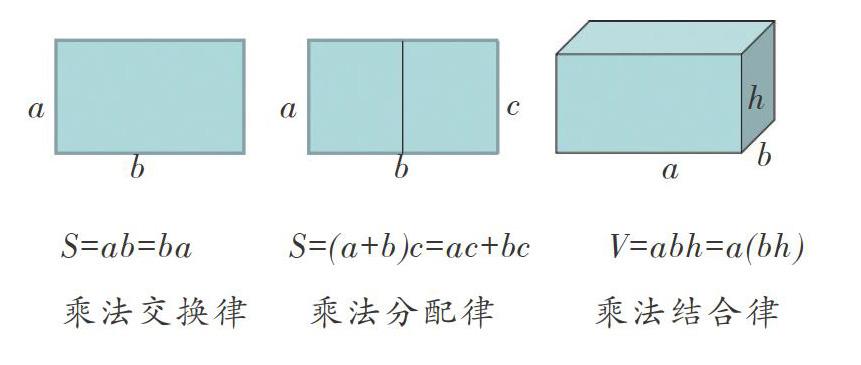
在教學中，有些比較抽象、難以理解的內容還可以和直觀形象、易于理解的圖形之間進行類比，兩者之間可以互相解釋，加深學生對這些內容的理解。比如，乘法交換律、分配律、結合律可以和下面圖形的面積、體積進行類比：

四、在解題方法指導過程中培養

教學中，教師應注重對解題方法相似的題目的數量關系進行梳理、類比，使學生弄清它們之間的聯系，加深對解題方法的理解。

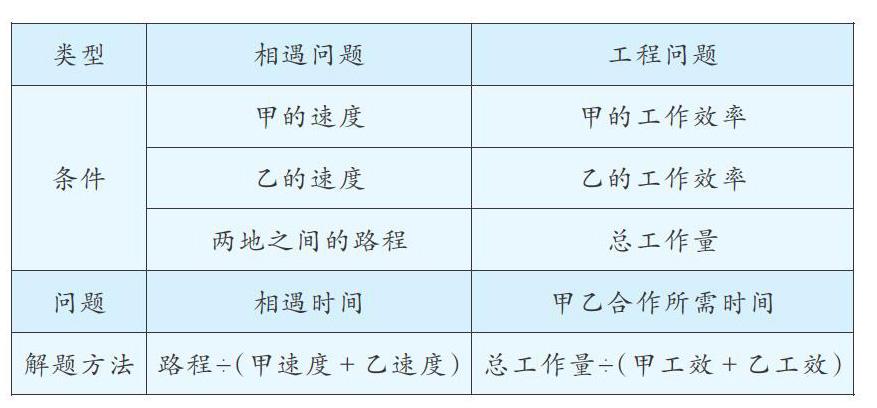
比如，相遇問題和工程問題的解題方法十分相似，教師可對這兩類問題進行類比：[類型 相遇問題 工程問題 條件 甲的速度 甲的工作效率 乙的速度 乙的工作效率 兩地之間的路程 總工作量 問題 相遇時間 甲乙合作所需時間 解題方法 路程÷（甲速度+乙速度） 總工作量÷（甲工效+乙工效） ]在解答較復雜的、難理解的題目時，教師可引導學生與同類型的基本題目進行類比。由于較復雜的題目中已知條件的本質特征具有隱蔽性，常常造成學生思維受阻。遇到這種情況，教師可引導學生把復雜題與同類型的基本題類比，揭示其結構特征，化難為易。比如，學生解答應用題“一匹布料用來做上衣可做30件，做褲子可做40條，現在用這匹布做了20件上衣后，剩下的布料還可以做多少條褲子”時，可能剛開始會沒有思路，覺得沒見過這類型的題目。如果教師引導學生和已學過的分數工程問題“一項工程，甲隊單獨做要10天完成，乙隊單獨做要12天完成。現在由甲隊先單獨做3天，剩下的任務由乙隊完成，乙隊還要做幾天才能完成這項工程？”相類比，學生就會茅塞頓開。

在學生掌握了某一種類型題目的解題方法后，教師也可設計一些變式題目讓學生來比較、分析，加深對解題方法本質的理解，培養學生的類比推理能力。

（作者單位：武漢市東湖風景區華僑城小學）

責任編輯? 張敏