在深度學習中生成核心能力

王華蓉

近日，筆者應邀在《湖北教育》第一屆“教研名師”觀摩課暨中小學生發展核心素養研討活動中主講了觀摩課——《平行四邊形的面積》。筆者從生活問題入手，引導學生經歷觀察、猜想、驗證、轉化、對比、遷移、推理、總結、應用等數學活動，獲得平行四邊形面積的計算方法，走向深度學習。

一、滲透思想方法

一是轉化、等積變形思想方法的滲透。數學思想方法是處理數學問題的指導思想和基本策略，是數學教學的靈魂。引領學生探究平行四邊形的面積計算公式時，教師要有機地把“數方格”的方法和轉化方法融為一體。

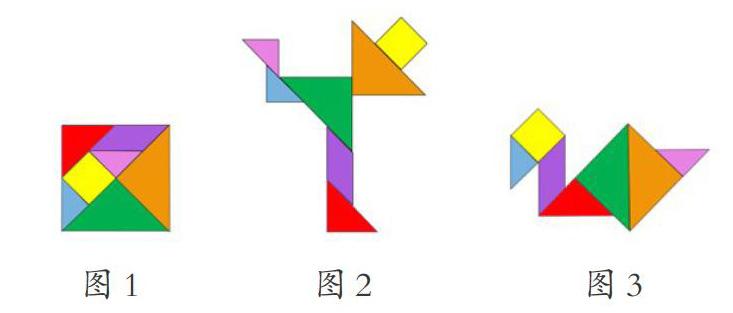
教學中，教師先用課件出示七巧板拼圖（圖1），得出規則的正方形的面積后，再出示兩個不規則的拼圖（圖2，圖3），問：“這兩個圖案的面積是多少？”學生通過觀察發現：圖2、圖3是把規則的拼圖轉化為不規則的拼圖，形狀變了，但面積不變。

接著，教師出示方格圖（圖4），提示學生，每個方格的面積為1平方厘米，不足一格的按半格計算，要求學生數出兩個不規則圖形的面積。學生數完后，教師展示學生數方格的方法，引導他們進一步感悟把不規則的圖形轉化成規則圖形的轉化方法。

二是空間觀念的培養。引導學生自主探究“平行四邊形的面積”中，教師不但要讓學生悟出把方格紙剪下來拼一拼，將不是整格的拼成整格，再數出平行四邊形面積的方法，還要讓學生通過畫一畫、剪一剪、移一移、拼一拼等方法，創造性地將平行四邊形轉化成長方形求面積，在變與不變中感受轉化方法，培養和發展空間觀念。教學中，教師先讓學生通過比較，發現長方形的長與原平行四邊形的底相等，長方形的寬與原平行四邊形的高相等，然后通過小組交流，推導、歸納出“平行四邊形的面積=底×高”。這樣教學不僅充分發揮了學生的主體作用，而且培養了學生的創新意識和空間觀念，提升了學生分析、綜合、比較、抽象和概括的能力。

二、充分體驗操作

核心素養下的課堂關注的是學生的體驗與感悟，以及知識背后所蘊含的數學價值。

當學生猜測“平行四邊形的面積=底×高”后，教師讓學生說說猜想的依據，然后引導他們去探索，去研究，去經歷知識的獲得過程。課前，教師給學生準備了大小不一的平行四邊形。課中，學生動手前，教師先引導他們思考：①你通過剪、拼，將平行四邊形轉化成了什么圖形？②你是怎樣剪、拼的？你是沿著什么剪的？學生操作的過程中，教師提示學生關注：“為什么要沿著高剪開，并且平移？”學生通過觀察、思考，發現要轉化為長方形，四個角必須都是直角，并且平移后兩腰重合才能保證底邊長不改變。學生在經歷、體驗、思考、分享的過程中，思維不斷生長，最終將新知轉化成舊知，根據長方形的面積計算公式推導出了平行四邊形的面積計算公式。

三、精心設計問題

問題是思維的起點。教學中，教師要精心設計問題，讓數學學習變得有深度。

引導學生推導平行四邊形的面積計算公式時，教師先提出問題：“把平行四邊形剪拼成長方形，應該怎樣剪？”學生經過思考，有的從左邊頂點往對邊剪，有的從右邊頂點往對邊剪。這是一般性的思維。教師再提出問題：“沿中間的某一個點往對邊剪，可以嗎？”當學生將手中的平行四邊形轉化成長方形后，教師又提出問題：“平行四邊形轉化成長方形后，什么變了？什么沒變？轉化后的長方形的長和寬與原來的平行四邊形的底和高有什么關系？”學生經過思考和辨析，知道平行四邊形轉化成長方形后，面積不變，形狀變了，轉化后的長方形的長和原來平行四邊形的底相等、寬和原來平行四邊形的高相等，進而根據長方形的面積公式推導出“平行四邊形的面積=底×高”。教師追問“是不是所有的平行四邊形都能轉化成長方形”，并播放不同形狀的平行四邊形轉化成長方形的微課，讓學生觀察、感悟、思考，明白所有平行四邊形的面積都可以用“底×高”來計算。學生經歷由特殊到一般的推理過程，在變中找到了不變：“因為平行四邊形的高有無數條，所以有無數種剪法;因為要剪拼成長方形，所以要沿高剪。”這樣的引導，使學生深刻認識到平行四邊形的面積與它的高有關。在此基礎上引導學生推導出平行四邊形的面積計算公式，自然就水到渠成了。同時，學生也發現所有平行四邊形的面積都可以用這個公式來計算，思維走向了更高的臺階。

四、適時引導思辨

學生經歷數學學習活動后，教師要引導他們思辨，讓其從學習活動中提煉出一些學習經驗，將感性認識上升為理性認識。

為什么會出現第一種算法呢？學生說，因為長方形的面積等于長乘寬，所以平行四邊形的面積也可以用鄰邊相乘的積計算。“平行四邊形的面積是不是可以用鄰邊相乘來計算？”教師以問題為內驅力，撥動學生的思維之弦。學生通過小組交流，發現平行四邊形的面積只能用相對應的底和高相乘。

又如：如圖6，把一個長方形框架拉成平行四邊形，平行四邊形和原來的長方形相比，面積變了嗎？

當這個問題呈現時，學生一下子得出兩種結果：“面積變小了”;“面積沒有變”。哪種結果對，為什么呢？學生思考后發現：平行四邊形的面積大小與它的底和高的大小有關。把長方形拉成平行四邊形后，雖然底沒變，但是高變小了，所以面積變小了，但它的周長沒有變。這種思辨，讓學生進一步感悟了轉化的數學思想方法，加深了對幾何圖形特征的認識和理解，提升了數學思維能力和空間想象能力。

（作者單位：武漢市光谷第21小學）

責任編輯? 姜楚華