優化學習方式 培養創新意識

王鵠

對小學數學課堂教學而言，基于核心素養下的深度教學是必然趨勢。如何通過單元整體教學促進學科能力走向學科素養，從而實現深度教學？

小學是培養學生創新意識和創新能力的關鍵時期。在小學數學課堂教學中，教師應當把學生的主體地位與作用前置，以獨立思考、自主探究、動手實踐、合作交流等方式進行深度教學。

一、由“看演示”變為“動手做”

動手操作是幫助學生理解知識、促進求異思維、培養創新意識的重要方式。

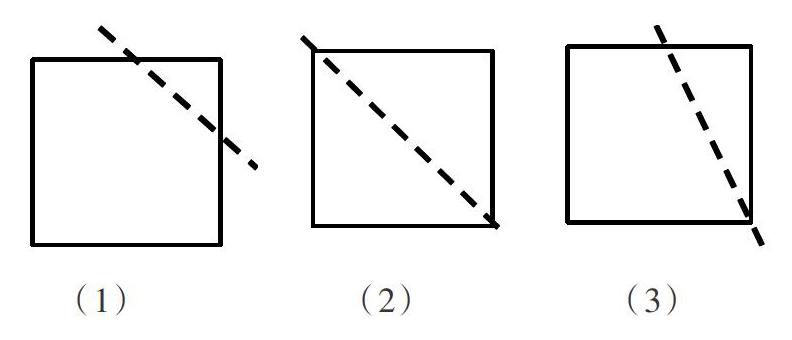
例如：在學生認識四邊形的特征后，教師出示一道趣味數學題：“一個正方形，剪掉一個角，還剩幾個角？”學生往往會憑直覺把“剪”當作“減”，用4個角減掉1個角得3個角。此時，教師適時提出質疑：“一定剩下3個角嗎？”待學生遲疑之時再提示解決方法：“實踐出真知。試著剪一剪，看你會有什么發現？”學生通過剪和數，以及組內交流、集體展示，總結出三種的操作方法及相應的結論（如下圖）：

第（1）種情況：從相鄰兩邊的中間剪掉一個角，剩下部分變成五邊形，所以剩下5個角;第（2）種情況：沿對角線剪，剩下一個直角三角形，所以剩下3個角;第（3）種情況：一端在角的頂點，另一端在對邊上，剩下部分是四邊形，所以剩下4個角。

這種集動手操作、分析思考、討論交流、總結提煉等多種方法為一體的深度學習活動，促進了學生思維的發展和創新意識的萌發。

二、由“聽講解”變為“試探究”

教學中，教師要善于滿足和利用學生這一心理需求，創設有挑戰性的問題情境，把數學問題的探索價值、探索時間和空間留給學生，鼓勵學生按照自己的認知能力和思維方式進行多角度地探索。

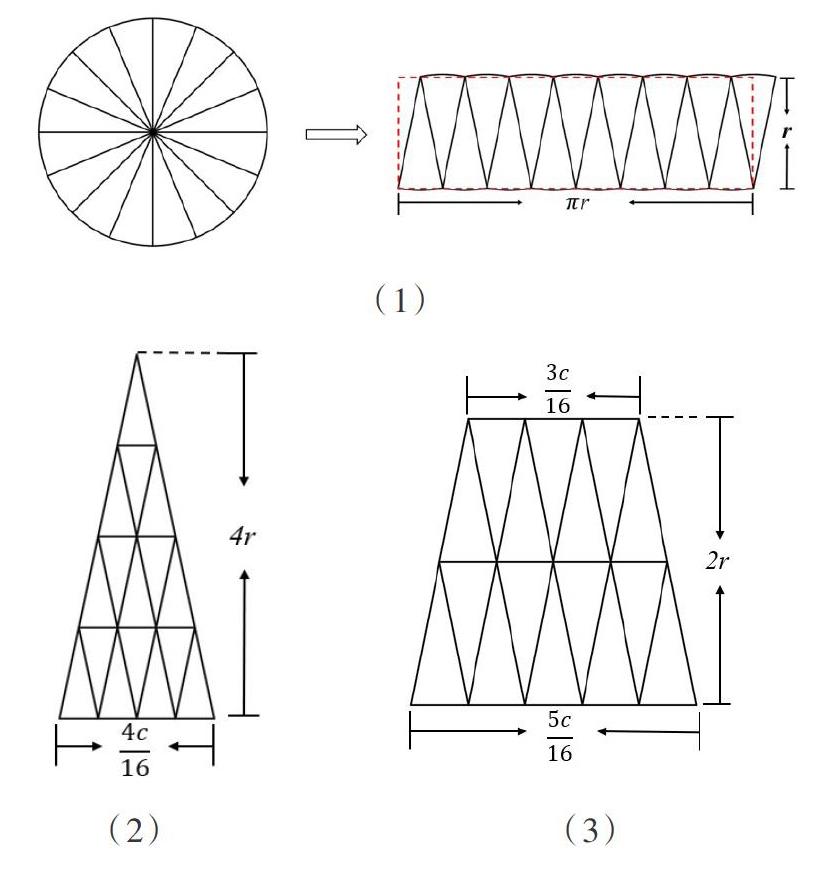
在教學“圓的面積”時，圓的面積計算公式的推導，對于學有余力的學生，不能局限于書本上提出的“把圓等分后拼成近似的長方形”的方法，而要引導學生運用轉化的思想，把新知識“曲線圖形圓”轉化為學過的“由線段圍成的多邊形”來研究。通過學習單的導學、小組合作的助學，學生理清了圓與轉化后的圖形之間相關聯的量之間的關系，得到以下三種推導方法（如下圖）：

（1）近似長方形的長是[π]r，寬是r，根據長方形的面積計算公式可得：S圓=S長=[π]r×r=[π]r2。

（2）近似三角形的底是[4c16=c4]，高是4r，根據三角形的面積計算公式可得： S圓=S三=[12]×[c4]×4r = [12]×[2πr4]×4r=[π]r×r=[π]r2。

（3）近似梯形的上底是[3c16]，下底是[5c16]，高是2r，根據梯形的面積計算公式可得：S圓=S梯=[12]×（[3c16 ]+ [5c16]）×2r=[12]×[c2]×2r=[12×π]r×2r =[π]r2 。

在以上圓的面積計算公式多樣化的推導過程中，學生經歷了拼組、觀察、對比、推理等活動，感悟到轉化、推理、極限等數學思想，積累了豐富的活動經驗，創新意識也在活動中得到強化。

三、由“口頭答”變為“記錄單”

用記錄單寫下思維過程，是一個相對獨立和完整的思維活動。它有利于培養學生個性化的思維方法、呈現解題思路。

教學中，教師要借助學習記錄單引導學生通過獨立或與同桌互助的形式，運用已有的知識和經驗自主思考解決問題，并記錄下思考過程和結果，內在的思維活動外顯化，為展示交流活動提供可視化的素材，促進后續對比、分析、質疑活動的深度開展。

在《分數除以整數》的教學中，學生根據問題情境列出兩個不同算式：[45÷]2和[45]×[12]。計算出[45]×[12]=[25]后，教師提出質疑：[45÷]2=[25]嗎？[45÷]2和[45]×[12]這個除法算式和乘法算式結果真的完全一樣嗎？你能否想辦法，調動你的數學知識儲備，證明一下呢？可以用以前學過的方法算一算，可以借助圖形畫一畫，還可以用手中表示[45]的學習紙折一折。學生經過獨立思考，在學習單上記錄下自己獨特的想法，教師選取并展示了以下幾種能代表大部分學生思路的方法：

（1）[45÷]2=[4÷25]= [25]

（2）[45÷]2 （[45]的一半，4÷2=2）=[25]

（3）[45÷]2=（[45]×[12]）÷（2×[12]）=[25][÷1] =[25]

（4）[45÷]2 =0.8÷2 =0.4 =[25]

（5）畫：

（6）折：

（7）折：

接下來，教師引導學生觀察、比較這些方法，在求同、求異、求聯中，深刻理解算理和算法。由學生的質疑“為什么乘[12]”，生長出新知：[ 12]是除數2的倒數;被除數和除數同乘[12]后除數變成1，就把分數除法轉換成了分數乘法;分數除以整數，可以直接乘除數的倒數，等等。至此，學生在充分的思維交流、碰撞中，再生出分數除以整數的計算方法，從個性記錄、對比展示，再到集體交流，學生思維的獨特性、深刻性得以發展。

四、由“獨自想”變為“小組議”

在課堂教學中，教師應積極推行小組合作的學習方式，在教學的重點、難點、關鍵點之處把握時機，組織學生小組合作，讓其在合作中解決問題，發展創新意識。

教學“百分數的應用（例5）”時，對于“某種商品4月的價格比3月降了20%，5月的價格比4月又漲了20%，這件商品的價格是漲了還是降了？變化幅度是多少？”這樣一個沒有提供商品具體價格的數學問題，學生表現出濃厚的探究興趣。有的學生提出商品3月的價格未知，無法解決;也有學生直接利用“降20%，再漲20%”的信息得出價格不變的結論。

在學生遇到“3月價格未知”的思維障礙之處，教師適時引導學生小組交流解決這一關鍵問題。學生討論交流后，知道借助“分數除法”中積累的經驗，用“假設法”解決此類問題，可以假設3月價格為具體的數值，可以是抽象的單位“1”，還可以假設為字母a等。有了解題思路，不同層次的學生選擇不同的方法驗證自己的猜想，變“線型”教學為“板塊”教學，有效地保障學生探究的時間與空間。在交流展示環節，學生分享了三種不同方法：

（1）假設此商品3月的價格是100元：100×（1-20%）=100×0.8=80（元），80×（1+20%）=80×1.2=96（元），（100-96）÷100=0.04=4%。

（2）假設此商品3月的價格是單位“1”：1×（1-20%）×（1+20%）=0.96，（1-0.96）÷1=0.04=4%。

（3）假設此商品3月的價格是a元：a×（1-20%）×（1+20%）=0.96a，（a-0.96a）÷a=4%。

在此基礎上，教師引導學生進一步討論：（1）三種不同的方法有什么相同之處？（2）為什么降價和漲價都是20%，商品的價格卻發生了變化？（3）如果漲、跌的幅度一致，那么先漲再跌和先跌再漲的結果一樣嗎？在問題的引領下，學生通過小組討論交流，不斷地探索與思考，掌握了利用假設法解決問題的方法。在此過程中，他們從數學本質上理解了各種假設法的合理性以及內在的一致性，體會變中有不變的思想探究意識和創新意識得以培養。

（作者單位：襄陽市襄州區教研室）