在辨錯改錯中提升數學能力

余洪慶

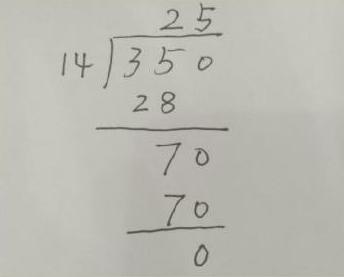
作業中的錯誤是教學的財富。教師應巧妙利用錯題資源，通過示錯、找錯、評錯、用錯等講評方式，培養學生觀察記憶、辨析思維、反思表達、發散創新等能力，提升學生核心素養。

一、在找錯中培養辨析思維能力

題目做對，答案一般是唯一的，題目做錯，卻各有各的錯誤。組織學生對錯誤進行辯析，在認識沖突中加深對問題的認識和思考，既能使學習變得更加有趣，又能發展學生的辨析與思維能力。

教學了《我們一起去游園》后，筆者出了這樣一道題：南門小學三年級有120名學生、15位老師、55位家長參加研學之旅，旅社社選擇哪種租車方案合適？A型車：限坐20人/輛，350元/天;B型車：限坐50人/輛，720元/天。

學生交流時，幾乎都選擇了3號方案，理由是沒有空位，最環保，節省錢最少。

師：為什么都不選1號方案？

生：1號方案花錢多，還空那么多座位，不合算。

師：事實是旅行社選定了2號方案。你認為旅行社選的方案合理嗎？如果你是旅行社經理，也會這樣選嗎？

生2：會選，2號方案價格只比3號多了20元，卻比1號便宜幾百元。

生3：2號方案，全部的人可比較平均地坐到4輛車上，4輛車人數差不多，公平又舒服。

生4：我認為，選2號方案，車是一樣，開出去一眼就能看出是一個團隊。

圍繞方案2的討論，讓學生思維的閘門一下子打開，體會到搞決策、做決定，要多方面權衡、考慮，不能只看某一方面。長期這樣訓練，能提升學生的辨析能力。

二、在評錯中培養反思表達能力

數學課標指出，在幫助學生克服困難、跨越障礙后，要及時幫助學生反思取得的成功經驗。學習了《乘法分配律》后，筆者有意安排了一道除法習題“350÷14”。全班學生出現了幾種算法：第一種算法是列豎式：

第二種算法是350÷14=350÷（2×7）=350÷2÷7;第三種算法是350÷14=（280+70）÷14=280÷14+70÷14;第四種是350÷14=350÷（7+7）=350÷7+350÷7。

獨立思考后，教師讓學生交流，格式如下：我同意（? ）的方法，不同意（? ）的，因為（? ）。學生交流的結果是，第一、二、三種方法正確，第四種錯誤。第一種算法正確顯而易見，學生用豎式算已經很嫻熟。第二、三種為什么對呢？第二種是把350先分2份，每份是175，再把175分7份，每份結果是25，也就是把一次性從350里面平均分14份，變為二次從350里面平均分14份，結果都是每份25。這就是除法性質的表述：從一個數里連續除以兩個數，等于用這個數除以它們的乘積。第三種把350分成280與70的和，這兩個數剛好都是14的倍數，確保都能剛好分完，先把280和70各自平均分成14份，分別得到每份20和5，再把各自平均分的結果合并，得到25。第三種算法還是緊扣除法的意義，保證分得結果的合理性和正確性。然而第四種算法是把350平均分成14份，轉變成兩次從350平均分成7份，不僅分的份數本身少了，每份結果變大了，而且還把變大的結果又合并一次，相當于又增加一倍，最后的得數就更大了。從除法的意義上說，這樣計算既不合情也不合理，結果出錯也就不足為奇了。

通過不斷地反思與表達交流，乘法分配律的知識在學生心中落地生根，他們真正理解內化了除法意義與運算律。

三、在用錯中培養發散創新能力

創新能力是數學學科的應有之意。培養學生具有敢于求異、勇于實踐、自主探索、發散創新的意識和能力，是教師的應盡之責。數學習題是培養這種品質和能力極有效的資源。六年級畢業總復習，教師為學生設計了這樣一道題：一根繩子長140m，先剪下20m做了5根長跳繩，照這樣計算，一共可以做幾根長跳繩？

大部分學生是常規做法：先算做1根長跳繩要多少米，再求總根數，即140÷（20÷5）=35（根）。少數學生是這樣做的：先算剩下的繩子能做多少根，再加上已做的5根得出總根數，即（140-20）÷（20÷5）+5=35（根）。有3名學生用乘法：先算140里面有幾個20，再算總根數，即120÷20×5=35（根）。有2名學生用倍比法：先求1m可做幾根，再算5÷20×140=35（根）。有8名學生用比例意義：140∶x=20∶5x=35。

有幾名學生，教師一發答題卡，他們就激動地喊：做出來了。筆者讓他們展示，他們的解法是：（140-20）÷（20÷5）=30（根）。筆者讓他們再審題，他們不好意思了，說題目求的是一共可以做幾根，自己做成了剩下的可以做幾根。

（作者單位：宜昌市遠安縣南門小學）

責任編輯? 張敏