此處“無聲”勝“有聲”

吳文祥

【摘要】“緘默知識”由英國哲學家波蘭尼提出，其認為緘默知識是更加微妙、不可言說的知識，是一種經常使用，但是不能通過語言文字符號直接傳遞的知識。在初中數學教學中，相對于顯性知識而言，教師對緘默知識的傳遞往往能夠實現一種此處“無聲”勝“有聲”的效果。文章對此做出了相關介紹。

【關鍵詞】此處無聲勝有聲;初中數學;緘默知識;傳遞

一、前言

數學是一門對學生理性思維要求很高的學科，很多知識與智慧是在無聲無息的積累中生成的。緘默知識又被稱為“內隱知識”，是人認識事物、解決問題過程中所依賴的一種理解和自信。在初中數學教學中，教師能夠將緘默知識有效地傳遞出去，往往可以實現一種此處“無聲”勝“有聲”的效果，對學生的數學成長發展會產生諸多裨益，是今后教師教學研究的重點。

二、感知存在是緘默知識傳遞的基礎

緘默知識是一種不可名狀的知識，它存在于人的認知過程中。在初中數學教學中，緘默知識雖然看不見，摸不著，但是無處不在。教師若想要對緘默知識進行傳遞，就必須要先使學生感知緘默知識的存在。學生只有認識到緘默知識是真實存在的，才愿意深入地挖掘緘默知識，并重視緘默知識的學習。如筆者在執教過程中，會通過“直接”和“間接”兩種形式幫助學生感知體會緘默知識的存在，從而實現此處“無聲”勝“有聲”的教學效果。

1.直接法

所謂“直接法”，主要是指教師通過想象比喻、生活轉換和PPT整合的方式，盡可能地將緘默知識形象化，從而促使學生理解緘默知識的含義，幫助學生直觀地認識緘默知識。如筆者就曾經用了這樣一個比喻直觀地闡述緘默知識：人在走路的過程中，有的人并沒有強化記憶，但是對于之前走過的路了如指掌;有的人努力記憶，卻猶如“路癡”，即使走了很多遍，也不記得走過的道路。這就是緘默知識的體現[1]。在解答數學問題的過程中也是如此。緘默知識就好比“思路”，有了緘默知識，可以快速地調取腦海中的公式法則，即使對于指向性不強的問題，也可以快速地得出答案。因此在初中數學學習過程中，緘默知識是無處不在的。像這樣的例子還有很多，在實踐教學過程中，教師要借助直接刺激的方式，幫助學生理解緘默知識的含義。

2.間接法

所謂“間接法”，就是讓學生在潛移默化的過程中感知緘默知識的存在，讓學生認識到緘默知識是數學世界中最美的知識。如英國數學家哈代就曾經說過：“數學的美是難以定義形容的，但是一種真實存在的美。”這其實就是數學緘默知識的美[2]。如在初中數學學習中，“對稱軸”“函數曲線”“平面幾何”都是存在一種真實之美的，這種美雖然用語言無法描述，但是在心靈上可以認知體會。在實際教學過程中，教師要不斷地對學生進行間接引導滲透，幫助學生感知緘默知識的存在，并體會到緘默知識是介于邏輯思維與直覺思維之間的一種思維形式。這種思維形式是學習數學知識的重要突破口，也是緘默知識真實存在的一種證明。

三、挖掘作用是緘默知識傳遞的保障

在初中數學學習過程中，緘默知識的學習是具有重要意義的。相比較顯性知識，教師對緘默知識的傳遞，更能實現一種此處“無聲”勝“有聲”的教學效果。在教育改革的新形勢下，教師要更新傳統守舊的教學觀念，注意對緘默知識的作用進行挖掘，推動學生數學學習的更好發展。對此，筆者提出以下幾個方面的建議。

1.概念教學，留有余地

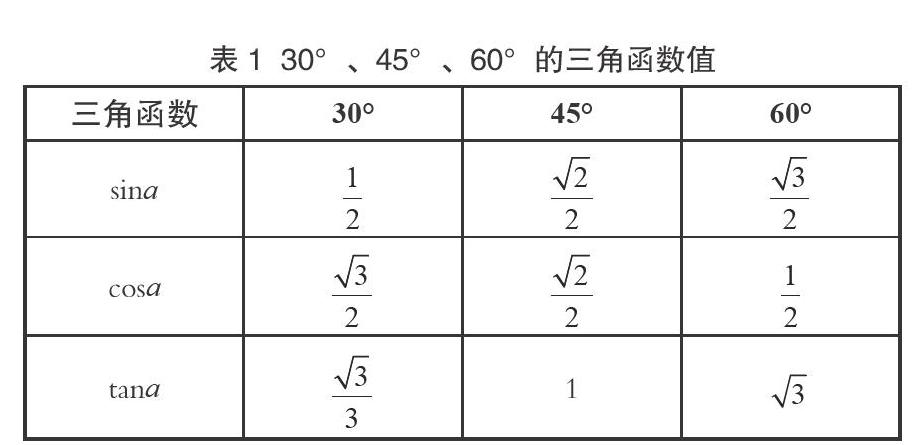
概念是數學知識的基本依據，在初中數學教學中，理解數學知識概念，是學生學好數學的先決條件，同時也是學生做題、解題的基礎。以往教師在對學生進行概念教學時，總是恨不得將所有的知識都展現出來，不留余地地全盤灌輸給學生。這種教學方式看似毫無保留，但由于沒有激發調動學生的主動思維意識，反而對教學效果造成了一定的負面影響。以“三角函數”知識教學為例，這一知識在中考計算題中的出現頻率很高。初中階段學生需要掌握30°、45°、60°特殊的三角函數值，如表1。

以往在講解這一知識時，很多教師都是將上述三角函數值直觀地展示出來，并讓學生進行背誦記憶，但在實際應用的過程中，學生還是容易混淆遺忘。而在緘默知識傳遞教學中，教師無需向學生出示三角函數值，只需將圖1所示的圖形展示出來即可，然后引導學生觀察圖形，借助兩個特殊直角三角形的特殊邊長自行求解，為學生提供一個獲取緘默知識的空間，從而通過圖形對照的方式，記憶不同角度對應的三角函數值。在這樣的教學方式下，知識不是教師直接喂到學生嘴里的，而是學生自己掌握和消化了知識概念，形成緘默知識，幫助學生形成永久性的記憶，可以幫助學生減少知識遺忘，為學生的學習提供了保障[3]。

2.數學閱讀，學會分析

閱讀不僅是語文或者英語學科的學習專利，初中數學學習中也是需要閱讀的。良好的閱讀能力是學生數學學習、理解的保障。然而在教學過程中教師都有這樣的心得體會，就是數學閱讀能力培養無從入手，無法對學生進行系統的指導，只能學生自己體會分析，這其實就是數學緘默知識傳遞的過程。

如在進行“垂徑定理”教學時，“垂直于弦的直徑平分弦，并且平分弦所對的兩條弧”叫作“垂徑定理”，這一定理內容雖然只有21個字，但是多數學生難解其意。雖然結合圖形教學可以在一定程度上改善效果，但依舊存在一定的局限性。對此，在傳遞緘默知識的教學中，教師可以采用這樣的方式對學生進行引導，如要求學生像閱讀古詩一樣，對 “垂徑定理”概念進行閱讀，如“垂直于弦的/直徑/平分/弦，并且/平分/弦所對的兩條弧”，這樣的閱讀方式能夠更好地幫助學生把握住定理內容中的關鍵詞，以及句子中主謂語之間的關系，然后教師再結合圖形指導閱讀，學生就會更加清晰地理解體會“垂徑定理”知識[2]。在這樣的閱讀分析引領下，學生可以自然而然地體會如何在閱讀中“抓重點”，從而促進學生數學閱讀能力的提升。除此之外，教師還可以傳授學生圈畫法、問題羅列法等提高數學閱讀能力的方法。這就是無形中將積累緘默知識方法傳遞給學生的一種體現。隨著學生閱讀能力的不斷提升，學生的數學學習之路也會走得更加順暢，從而實現了一種此處“無聲”勝“有聲”的教學效果。

3.問題解決，重視方法

在初中數學教學中，很多教師都反映學生的解題能力不強。導致此種現象的重要原因就是學生缺少緘默思維。可以說，在解決數學問題時，緘默知識的運用是解題的第一步，具有緘默知識的學生會自己思考“如何解決”，從而快速地確定解題思路，找到解題的突破口。

例如：“在直角坐標系xOy中，點O的坐標為（0，0），有一個動點A，坐標為（t，t），在第一象限，動點B（0，m）在y軸上。當AB=4時，問△OAB面積的最大值為多少？”在解答這樣的數學問題時，大多數學生根據自身的緘默知識，第一反應就是建立直角坐標系，但是在建立直角坐標系之后發現無法更進一步解題，因此陷入解題困境。正確的解題思路應該為將O、A、B三點置于圓中，當點O到AB的垂線段經過圓心時，此時的三角形面積就是最大的。而在對學生進行緘默知識傳遞時，顯然不能直接將這一解題思路告知學生，教師可以通過側面引導的方式，逐步地幫助學生建立解題思路。

如教師可以引導學生做出這樣的思考，即△OAB中∠O是一個固定值45°，AB的長度4也是確定的，只有點O是一個動點，它與AB的位置關系不斷地發生變化，正是因為有了這樣的變化，△OAB的面積才發生了變化。問題轉化為：在圓中長為4的定弦AB所對的圓周角∠O是45°，求動點O到直線AB的最大距離。這樣的引導會讓學生思考“是什么元素決定了三角形的面積呢？”在思考的過程中，學生就會逐步樹立正確的解題思路。這就是教師向學生傳授緘默知識的一種體現。

在整個初中階段的數學學習中，解題方法很多都是固定的，如直接法、補形法、分割法等。緘默知識的傳遞，使學生對解題方法進行積累，對學生的數學學習成長有諸多裨益，可促使學生的解題能力不斷提高，實現此處“無聲”勝“有聲”的教學效果。

四、結語

相比可以直接用語言、文字、符號直接表達的顯性知識，緘默知識則隱形地存在于人的認知過程中，其雖然“不可名狀”，但是是真實存在的。在初中數學教學中，教師對緘默知識進行傳遞，可以更好地幫助學生領悟知識精髓，實現一種此處“無聲”勝“有聲”的教學效果，因此緘默知識傳遞是值得今后廣大初中教師同仁探索研究的課題。

【參考文獻】

[1]薛峰.此處“無聲”勝“有聲”——淺談初中數學教學中緘默知識的傳遞[J].數學教學通訊，2019（14）：38-39，51.

[2]李光友.此時無聲勝有聲——淺談初中數學問題教學中學生思想品質的培養[J].學生之友（初中版）下，2016（07）：67.

[3]陸一黎.此時無聲勝有聲——緘默知識在美術教學中的運用淺探[J].中國美術教育，2011（03）：4-7.

[4]曹焱.發展學生數學素養，“板書”無聲勝有聲——結構式板書在初中數學素養教學中的探索與實踐[J].數學教學通訊，2019（11）：74-76.