淺析初中數學圖形變換的教學策略

李文莉

摘要：在初中平面幾何教學中運用好圖形變換，讓學生認識各種圖形的變換模式，并配合好實際動手操作，從不同的角度帶領學生學習平面幾何知識。這樣不僅使學生站在運動變化的高度來學習平面幾何，而且還有助于學生建立正確的審美觀，發現圖形世界的美妙，激起探索的欲望，激發學習的興趣;同時也突出素質教育改革的重要作用。

關鍵詞：初中幾何;圖形變換; 新高度;思維靈活

初中幾何教學一直以來都是初中數學的教學難點之一，一方面是由于初中幾何與小學的數學知識結構有較大的差別，需要學生有一定的適應能力;另一方面，是由于平面幾何是以圖形為主體的，需要學生對幾何圖形有較敏感的思維和一定的圖形推理能力，而這些都是初中生所欠缺的。因此，要做好初中幾何教學需要教師在教學中運用多種教學方式來引導學生思考，培養學生的幾何思維。因此接下來將談談圖形變換在初中幾何教學中的應用，通過圖形變換，讓學生站在新的高度來認識圖形、學習幾何知識、探究幾何圖形的性質和規律。

一、通過圖形變換的多樣性，培養學生從多角度思考問題

在初中數學教學過程中，所謂圖形變換就是指許多點的集合，是某一個幾何圖形關于某一點的變換，這一點不僅存在于原來的圖形中，在變換后的圖形中也能找到相對應的位置。圖形變換可以分為兩種形式，一種是全等變換，一種則是相似變換，即平移、旋轉、軸對稱、相似變換等。圖形變換實質上是從圖形運動的角度去看待圖形，具有非常靈活的變化和豐富的樣式。在平面幾何教學中加入圖形變換，有助于學生從不同的角度來掌握圖形的結構特征，培養學生的多角度思維，也為學生的空間思維做好鋪墊。

例如，學生在進行健美操運動的時候，便可以研究下哪些動作是軸對稱變換，那些又是平移變換或是旋轉變換。再如，在學習人教版初中數學八年級下冊有關“平行四邊形”的知識，對于平行四邊形ABCD中的“AB=CD，AB∥CD”就可以引導學生從不同的角度來認識：

角度1.站在圖形的位置關系和數量關系來認識圖形關系;

角度2.從平移變換的角度來看，把線段AB沿AD方向平移，移動AD個單位就可以得到DC，所以有AB=CD，AB∥CD;

角度3.站在中心對稱的角度來看，把AB以O點為中心，旋轉180°后，就可以得到DC，因此有AB=CD，AB∥CD。

二、通過圖形的變換性質教學，使學生站在新高度來認識平面幾何

在日常教學中，先讓學生從基礎的圖形性質入手，學習和探究圖形的性質的來由和應用范圍，形成圖形變換的初步認識。接著，再引導學生從圖形的變換性質來深入認識圖形，并由此及彼認識其他圖形性質。通過探究圖形的變換性質，不僅能加深學生對基本圖形性質的理解，還能使學生站在新高度來認識平面幾何。

例如，在學習人教版初中數學九年級上冊有關“圓”的知識。學習過基本知識后，學生能掌握圓是軸對稱圖形也是中心對稱圖形，這是非常特殊的圖形。下一步，教師可以引導學生從這些特殊性質入手，經過變換，得出圓的其他性質，比如，垂徑定理，所有的直徑都經過圓心，就可以由軸對稱性質和中心對稱性質得到。用這樣的方法來講解，更加直觀和簡便，并且學生能將圓的性質應用到其他領域。同樣，在學習三角形和四邊形時，也能應用“軸對稱”性質的變換，去探究它們的圖形性質。

三、通過實際動手操作圖形變換，增加學生的直觀感受和推理能力

幾何圖形的變換多樣，通過讓學生動手操作真實圖形的變換，能讓學生在直觀上感受圖形的形狀和對稱、平移、旋轉等性質，在探究中形成平面幾何圖形的動態印象，增加學生的空間想象能力和圖形推理能力。

例如，在學習人教版初中數學八年級上冊有關“等腰三角形”的知識。教師在課堂上，讓學生自己畫出等腰三角形，并剪出來，然后通過對折，直觀地感受等腰三角形的兩個底角相等，兩條邊相等的，認識到等腰三角形是以底邊上的高為對稱軸的軸對稱圖形。通過折痕教師還能引導學生探究“三線合一”，即底邊上的高、頂角的角平分線、底邊的中線是重合的。這樣的動手過程，學生更直觀形象地感知這個性質，比教師用幾何知識來證明這些性質要來的更實際，學生更容易接受和理解。教師也可讓學生動手繪制圖形變換的過程，在教師講解圖形變換課程的時候，引導學生繪制圖形變換的過程，了解圖形變換的特點，在繪制圖形變換過程的時候鞏固和梳理所學到的知識，以發散學生的思維，提高學生的動手能力，通過所繪制的圖形來尋找對稱軸的位置。例如教師在教學過程中，可以讓學生在方格中先繪制一個三角形，然后再將三角形平移，重新繪制出一個新的三角形，然后可以讓學生數相隔的方格數量，以便掌握三角形平移的單位。在初中數學圖形變換的過程中，既要幫助學生了解圖形變換的含義和概念，也要注重學生數學邏輯思維推理能力的培養。

四、通過圖形變換，有助于提高學生的思維靈活性

在幾何題目中，已知的幾何條件往往比較復雜而分散，要理清這些關系才能整合題目的條件，為下一步作出結論和判斷提供依據。這里就可以利用圖形變換，使分散的圖形集中起來，使復雜的條件變得有條理，還可以挖掘出題目的隱含條件。通過變換，找出動態變換題目中數量的變化關系，找到變化規律，使題目得以化解。在這訓練過程中，有助于提高學生的思維靈活性。

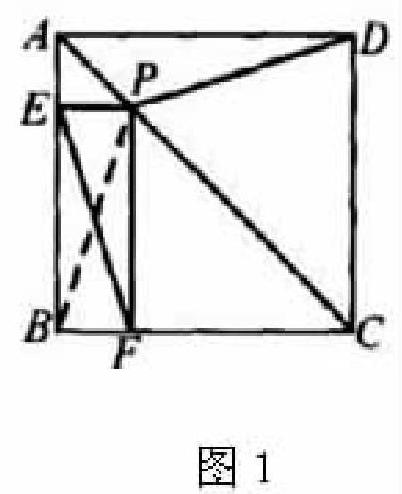
例如，如圖3所示，正方形ABCD，對角線AC上的一點P，過P作PE⊥AB于E，作PF⊥BC于F，連結EF。試判斷EF和DP的數量關系，并說明理由。

由題意可知，題目涉及正方形，那么正方形的許多性質就可以變換為已知條件，來輔助證明。題目要證明數量關系，可以大膽猜測是相等的。那么就要證明全等三角形或者證明平行四邊形，由此可以延長EP交CD于G，證明Rt△PDGRt△FEP，如圖3左圖;也可以用對稱軸，連結PB，則DP和PB，關于AC對稱，用PB作為中間變量來證明，如圖3中圖;還可以用旋轉來做，將Rt△FEP順時針轉90°，得到Rt△GHP，再來證明四邊形AGHP是平行四邊形即可。

五.通過多媒體展示，簡化圖形變換，有助于學生掌握圖形變化技巧。在初中數學圖形變換教學中，教師可以充分利用多媒體教學技術，利用多媒體教學技術來向學生展示圖形變換的動態過程，以幫助學生理解圖形變換的規律和性質，掌握圖形變換的技巧。另外，教師還可以利用生活中的事例來幫助學生研究和理解圖形變換。例如在講解軸對稱圖形的時候，教師可以通過教師的窗戶或是門、黑板等來將其簡化成幾何圖形，然后來尋找其對稱軸。

總地來說，在初中平面幾何教學中運用好圖形變換，讓學生認識各種圖形的變換模式，并配合好實際動手操作，從不同的角度帶領學生學習平面幾何知識。這樣不僅使學生站在運動變化的高度來學習平面幾何，而且還有助于學生建立正確的審美觀，發現圖形世界的美妙。總之，加強對初中數學中圖形變換相關教學的研究，具有重要的意義。教師在教學過程中要突出學生的主體地位，培養學生對圖形變換這一課程的學習興趣，調動學生的學習積極性，以促使學生進行自主的學習，激發學生的學習欲望，使其能夠自行發現問題、探索問題。

主要參考文獻

[1]沙雷金等. 直觀幾何[M] .上海;華東師范大學出版社 .2001 .

[2]劉長明，孫連舉. 中美兩國數學課程標準中初中學段“空間與圖形”領域的內容標準之比較[J] .數學教育學報，2002（11） .

[3]蘆淑坤. 圖形與變換課程內容的教科書呈現研究[D] .吉林：東北師范大學 .2006 .