平面向量數量積課堂教學的反思與重構

程仕然

[摘 ?要] 文章對向量數量積課堂教學中內容銜接問題、物理背景引入問題和如何發展學生抽象素養問題進行反思. 在反思的基礎上，重塑概念產生的過程，發展學生數學抽象素養，“落實四基，發展四能”來進行課堂重構，并對課堂教學進行實錄.

[關鍵詞] 課堂教學;反思;重構;向量數量積

問題研究緣起

我校特級教師蔣智東老師曾上過一節“平面向量數量積”的公開課，并寫了篇實錄及反思文章[1]（下稱文1），至今仍被同行所津津樂道. 今年筆者在上這節課前，向蔣老師進行了請教和交流.蔣老師認為，新的課程標準更關注數學學科核心素養的形成和發展，更重視學生學習的過程. 所以，上過的那節課還有很多地方需要反思改進，建議重塑概念產生的過程，發展學生數學抽象素養，本著“落實四基，發展四能”來進行重構.

關于本節教學內容的若干反思

針對本節內容，筆者再次認真學習了教材，學習了課程標準.結合蔣老師的文1，重點對向量知識板塊的內部銜接及數學文化滲透、物理背景引入、如何培養數學抽象素養等方面進行了反思和研究.

1. 關于向量知識板塊的內部銜接及數學文化滲透的思考

文1的“情景創設”部分：

問題1：物理學中，向量的運算比較多，比如求位移、速度、合力的大小等，用到了向量的加法、減法和數乘運算，那么，物理中還有沒有其他的向量運算呢？

設計意圖：本課通過物理學中的求功運算來創設教學情景，使學生自然提出問題：求功運算與數學知識有怎樣的聯系？

蔣老師緊扣課程標準，通過向量豐富的物理背景，從位移、速度、合力的大小等實際情境入手，理解向量的概念與運算法則，快速進入主題. 在實際的課堂教學中，這種方式是實用有效的，也是值得學習和借鑒的.

2. 關于教材向量數量積概念的物理背景引入的思考

在實際的教學實踐中，向量這一部分內容往往放在高一下學期進行學習，課本上，這節課是以物理上功的運算這一物理模型進行引入展開的. 但這個時候學生物理上對功的學習也是剛剛展開，并且物理課本上是這樣介紹功的：用F表示力的大小，用l表示位移的大小，用W表示力F所做的功，……，當力F的方向與運動方向成某一角度（α），……，所以W=Flcosα，這就是說，力對物體所做的功，等于力的大小、位移的大小、力與位移夾角的余弦這三者的乘積[2].

用物理背景引入，存在物理學科描述和數學學科描述的符號及說法上的不同.如上面所說，物理中，用“F”表示力的大小，用“l”表示位移的大小，而沒有用F和l表示，這在學習之初，多少給學生帶來困擾.

3. 關于本節內容在課堂教學中培養數學抽象素養的思考

文1關于數學抽象部分：

問題4從求功的運算中，可以抽象出什么樣的數學運算？

教師指出數學抽象的方向：舍棄抽象原型的物理意義，抽取其中的數量關系.

平面向量的數量積

（1）最初的認識

學生討論：把力F和位移S抽象地看成兩個向量a和b，把力F和位移S的夾角θ看作向量a和b的夾角，就可以得到一種新的運算，它是從向量a，b得到一個數量（即abcosθ）的運算.

（2）進一步表述

引進“向量的數量積”等術語后，就可以把上面的結果進一步表述為：

已知兩個向量a和b，它們的夾角為θ，我們把數量abcosθ叫做a和b的數量積（或內積），記作a·b，即a·b=abcosθ.

蔣老師以問題驅動思考，步步深入，從物理“功”抽象出數學平面向量的數量積運算，實現概念的自主建構，也讓學生領悟到數學的發展源于實踐.這種學習方式是建立在從物理到數學的“聯想”基礎上的.

我們知道，數學抽象是指通過對數量關系與空間形式的抽象，得到數學研究對象的素養. 主要包括：從數量與數量關系、圖形與圖形關系中抽象出數學概念及概念之間的關系，從事物的具體背景中抽象出一般規律和結構，并用數學語言予以表征[3].

與前面所學的向量運算結果不同，向量的數量積的結果不再是向量而是數量，學生是首次接觸像這樣運算結果與運算對象不是同一范圍的運算. 如果設計一個微探究，讓學生自己在熟悉的數學內容中抽象出新的數學內容，讓學生充分經歷和體驗“發現定義”的過程，領悟數學發展的內部需求，不是更能激發學生的探究興趣和積極性嗎？

向量數量積課堂教學重構

1. 向量數量積課堂教學重構的指導思想

（1）重塑概念產生的過程，發展學生數學抽象素養，“落實四基，發展四能”;

（2）多一點數學文化熏陶，多一點數學本質探索，多一點數學素養培養.

2. 重構后向量數量積課堂教學實錄

師：同學們，通過前面的學習，我們知道向量兼具“數”與“形”的雙重形態，是溝通幾何與代數的橋梁. 其實，前面，我們已學習了向量的概念及表示、線性運算和坐標表示，這些內容的產生和發展經歷了漫長的時間. 大致可以分為三個階段：向量1.0原始版：古希臘的亞里士多德已經知道兩個力的合成，可以用平行四邊形的法則得到，這點向量知識，形成不了多少有意義的問題，只是向量的原始萌芽形態[4]. 向量2.0社會版：牛頓第一次用有向線段表示向量;平面向量基本定理的出現，使得向量可以用兩個非零向量進行分解，形成了一簇向量，相當于一個社會. 向量3.0高科技版：當時間進入十九世紀時，哈密爾頓引進新運算，溝通了代數、幾何與三角函數，諸多幾何問題都可以用向量方法“一攬子”解決了，向量進入了“高科技時代”.

我們將通過下面的學習來揭開“高科技版”的面紗.

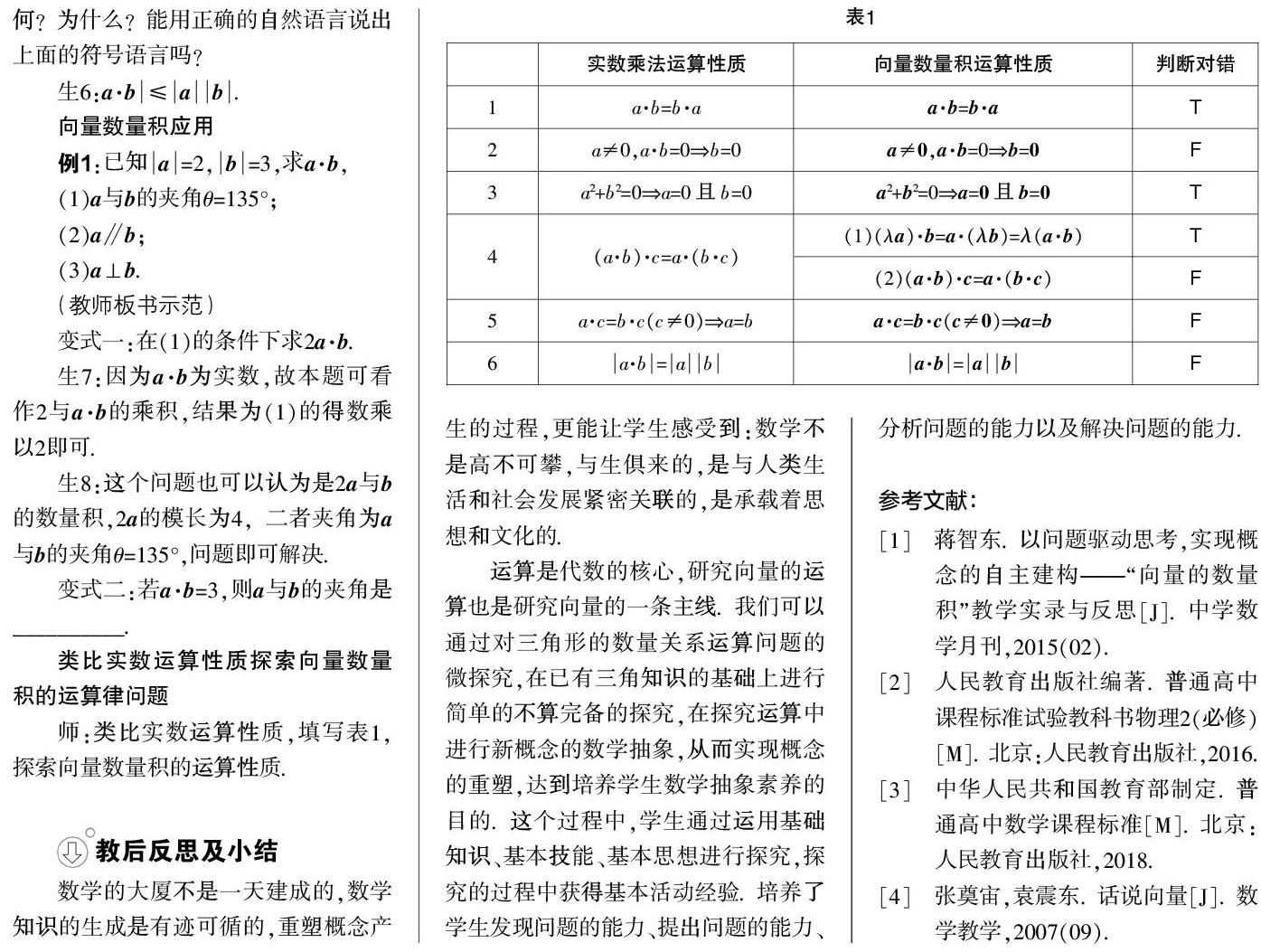
師：類比實數運算性質，填寫表1，探索向量數量積的運算性質.

教后反思及小結

數學的大廈不是一天建成的，數學知識的生成是有跡可循的，重塑概念產生的過程，更能讓學生感受到：數學不是高不可攀，與生俱來的，是與人類生活和社會發展緊密關聯的，是承載著思想和文化的.

運算是代數的核心，研究向量的運算也是研究向量的一條主線. 我們可以通過對三角形的數量關系運算問題的微探究，在已有三角知識的基礎上進行簡單的不算完備的探究，在探究運算中進行新概念的數學抽象，從而實現概念的重塑，達到培養學生數學抽象素養的目的. 這個過程中，學生通過運用基礎知識、基本技能、基本思想進行探究，探究的過程中獲得基本活動經驗. 培養了學生發現問題的能力、提出問題的能力、分析問題的能力以及解決問題的能力.

參考文獻：

[1] ?蔣智東. 以問題驅動思考，實現概念的自主建構——“向量的數量積”教學實錄與反思[J]. 中學數學月刊，2015（02）.

[2] ?人民教育出版社編著. 普通高中課程標準試驗教科書物理2（必修）[M]. 北京：人民教育出版社，2016.

[3] ?中華人民共和國教育部制定. 普通高中數學課程標準[M]. 北京：人民教育出版社，2018.

[4] ?張奠宙，袁震東. 話說向量[J]. 數學教學，2007（09）.