信息技術在高中數學教學中的應用研究

殷開勇

摘?要：將信息技術與高中數學教學活動整合在一起，不僅可以將數學圖象變得直觀、形象，便于學生的理解與觀察，而且還可以激發學生的數學學習興趣，提升學生學習的能力。本文結合課堂教學實例，談談信息技術在高中數學教學中的實際應用。

關鍵詞：信息技術;幾何畫板;高中數學;課堂教學

中圖分類號：G633.6??????????文獻標識碼：A ????文章編號：1992-7711（2020）01-102-2

現代社會已經逐步進入了信息技術時代，多媒體技術的發展日新月異，而多媒體教學也應運而生。一批優秀的教學軟件如幾何畫板、GeoGebra等被越來越多地運用到了數學的課堂教學中來。今天，我就以幾何畫板為例，淺談如何將信息技術與高中數學教學有機整合在一起，

一、信息技術在概念教學中的應用

在某些章節的概念教學中，如果借助于信息技術，可以為學生的學習營造出更合適的教學環境，可以更真實地還原數學思維過程，讓學生通過自己的探究與觀察，親身體會數學概念的形成及發展的過程，從而將機械的、抽象的數學概念變得直觀、形象，更容易接受及理解。在學習圓錐曲線這一章內容的時候，學生對于拋物線可能相對熟悉一些，但是橢圓和雙曲線的概念對于學生來說就過于抽象了。如果照本宣科地讀一遍定義，學生可能也能記住，但是這個記憶層次是淺顯的，因為學生根本就不明白為什么滿足這個定義的曲線就是圓錐曲線了。

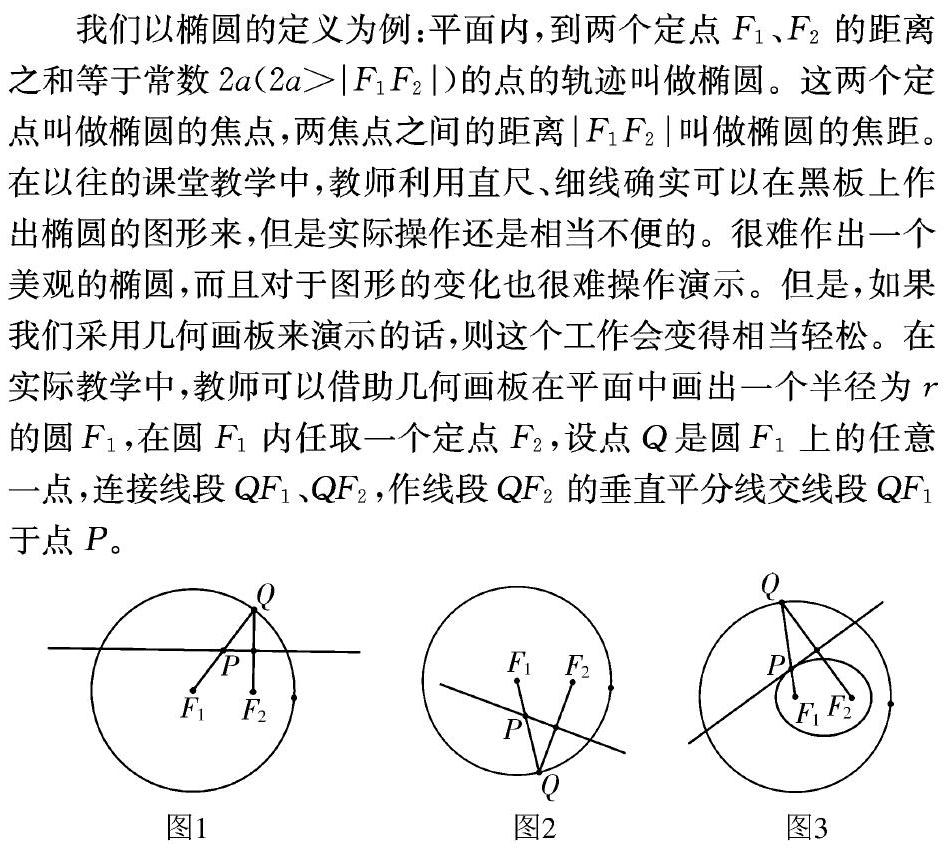
我們以橢圓的定義為例：平面內，到兩個定點F1、F2的距離之和等于常數2a（2a>|F1F2|）的點的軌跡叫做橢圓。這兩個定點叫做橢圓的焦點，兩焦點之間的距離|F1F2|叫做橢圓的焦距。在以往的課堂教學中，教師利用直尺、細線確實可以在黑板上作出橢圓的圖形來，但是實際操作還是相當不便的。很難作出一個美觀的橢圓，而且對于圖形的變化也很難操作演示。但是，如果我們采用幾何畫板來演示的話，則這個工作會變得相當輕松。在實際教學中，教師可以借助幾何畫板在平面中畫出一個半徑為r的圓F1，在圓F1內任取一個定點F2，設點Q是圓F1上的任意一點，連接線段QF1、QF2，作線段QF2的垂直平分線交線段QF1于點P。

此時教師可以提問：如果點Q在圓上繞著圓周運動的話，那么點P的運動軌跡如何？（如圖1）。在學生作出自己的判斷以后，教師可以拖動點Q在圓周上變化，演示點P的變化規律便于學生觀察（如圖2）。最后，教師同時選擇若P，Q兩點，利用構造軌跡功能，得到圖3所示的P點的軌跡。借助圖3，教師可以提問：在該變化過程中的恒量是什么？變量是什么？你可以總結出橢圓的定義是什么嗎？在具體教學中，學生興致勃勃地猜測點P的運動軌跡，當他們發表意見后，教師就可借助幾何畫板生動演示，學生很容易就能明白各個數量之間的關系，并能較為準確地總結出橢圓的定義。

二、信息技術在函數教學中的應用

三角函數這一章也是高中數學里相當重要的內容，是高考的必考知識點之一。這一章節中有很多內容都具有較高的概括性與抽象性，不利于學生的理解和掌握。因此，在課堂教學中，教師可借助幾何畫板在作圖方面的優勢，將抽象的三角函數具體化、形象化，使學生有機會親自參與到數學知識的探究與應用過程中來。信息技術借助抽象、歸納、類比、實驗、觀察等方式使得學生感知到創造數學知識的趣味性，并調動他們學習數學知識的積極性，從而促使他們在親自操作中不斷提高自身的建模意識、協作能力及操作能力。

下面我們以蘇教版必修4第一章1.3.3 函數y=Asin（ωx+φ）的圖象為例，來說明各個參數A、ω、φ的變化對函數圖像的影響。教師可以在同一坐標系中作出以下三個函數的圖像：f（x）=sinx，g（x）=12sinx，h（x）=2sinx。可讓學生判斷這三支圖像之間的聯系。利用圖像，此時學生可以大概作出正確判斷。

為了驗證我們的猜想，此時可以作出一條垂直于x軸的直線l，標記l與三個函數圖像的交點分別為A、B、C，并顯示出三點的坐標。拖動直線l左右移動，得到如上圖所示的三組坐標。此時，教師可引導學生分析參數A的改變對于原函數圖像的影響，哪些量不變，哪些量改變。如此，我們可以很容易地驗證我們的猜想并作出正確的歸納總結。同樣，我們可以借助圖像得出另外兩個參數ω、φ的改變對于函數圖像的影響。在此過程中，教師可引導學生自己動手，分別作出各個函數的草圖，激勵學生深入分析圖像的“形”與對應的“數”之間的關系，從而幫助學生找出曲線上的點所具有的規律性。教師可借助多媒體設備的動畫演示功能展示圖像動態變化過程，使學生更直觀體會變換規律的特點。

三、信息技術在函數解題中的應用

在數學教學中，問題始終處于核心地位。數學概念、數學方法、數學思想及數學知識均是在解決具體問題的過程中發展與形成的。所以，如何解決具體問題，便是我們能否學好數學的關鍵所在。在2019年江蘇高考數學試卷中，填空題的壓軸題第14題便是一道函數題。它涉及到的思想方法有數形結合思想、函數與方程思想;涉及到的知識點有函數的奇偶性、周期性、直線與圓的位置關系等。下面，我們便來看看如何利用幾何畫板解決此題。

首先，我們可以利用幾何畫板作出f（x）在區間（0，2]上的圖像，這是一個圓的上半部分，再利用奇函數的性質作出其在區間[-2，0）之間的部分，兩者關于原點對稱。而區間[-2，2]長度為4，正好是函數的一個周期。再利用函數的周期性可以得到所需要的區間（0，9]上的函數圖像，如下圖：

在高中數學教學活動中，信息技術不僅能方便快捷地作出函數圖像，還能動態地演示圖像的變化。教學實踐表明，信息技術與傳統的教學方法相比，更為生動直觀，可以提高學生探究函數、研究函數的興趣，有助于他們更精準感知并掌握相關解題方法。總之，將信息技術與高中數學教學恰當地整合在一起，可以有效地提高教師的課堂效率，幫助學生更好地把握數學知識的本質與規律，有助于學生解答數學問題能力的提高，因此，教師依據教學內容的需要，恰當應用信息技術，可以切實有效地提高數學教學效果。

[參考文獻]

[1]王玉飛.高中數學函數教學與信息技術的整合案例分析[J].中國教育技術裝備，2015（15）.

[2]彭瑞.信息技術與高中數學教學的整合[D].延安：延安大學，2016.

[3]郭超俠.信息技術與高中數學教學的整合案例研究[J].中國信息技術教育，2015（21）.

（作者單位：蘇州市吳江區平望中學，江蘇 蘇州215000）