例說高考函數壓軸題中的放縮策略

江蘇省無錫市洛社高級中學

縱觀近三年的全國卷試題,零點問題是函數壓軸題中的常客,每年都考.此類問題將函數、不等式、方程等知識綜合在一起,靈活多變,能有效地區分出學生在數學能力上的不同水平,故而廣受命題者青睞.從知識層面看,零點存在性定理是解決這類問題必不可少的工具,而應用該定理的關鍵在于構造異號函數值,這是頗具技巧性的一步.標準答案常給人眼前一亮的感覺,讓筆者驚嘆背后蘊含的解題智慧.然而,解法固然精妙,卻略顯突兀,難以推廣.

波利亞說過:“掌握數學就意味著學會解題”.筆者認為,解法是否自然,是教會學生解題的一個很重要的因素.基于這樣的觀點,經過深入的思考和實踐,筆者發現并總結出解此類題的一種方法,簡稱為放縮.這一方法的適用范圍更廣,不僅能處理零點問題,在其它函數問題中也有應用,符合解題教學提倡的“注重通性通法,淡化特殊技巧”.下面通過具體問題的分析,介紹幾種常用的放縮策略.

一 觀察結構,代數變形

通過觀察,發現式子的結構特征,與熟悉的代數公式產生聯系.這種情況下,可先做一點代數上的變形,給接下來的放縮帶來方便.

題目1(2018年高考全國2卷文科第21題)已知函數

(1)若a=3,求f(x)的單調區間;

(2)證明:f(x)只有一個零點.

解僅討論第二問.

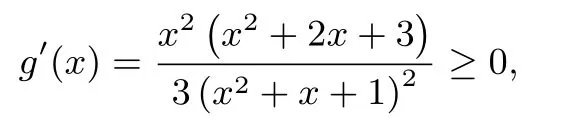
從而g(x)在(-∞,+∞)單調遞增,故g(x)至多有一個零點.

思路分析先分離a,將f(x)的零點轉化為g(x)的零點,便于求導討論單調性.從g(x)的結構聯想到公式……