怎樣的四面體能夠補成長方體?—-談補形法求解四面體外接球問題

湖南省懷化市鐵路第一中學

近年來求多面體的外接球問題在高考試題、各地模擬試題中頻頻出現,成為了熱點問題,其中四面體的外接球問題最具代表性.求四面體外接球問題的兩種常用方法一是截面法,即找球心求半徑;二是補形法,即將四面體補成長方體(四面體的所有頂點均為長方體的頂點),也就是等價轉化為求長方體的外接球問題.通過檢索大量的文獻發現,寫四面體外接球問題的文章不少,而且必然會提到上述兩種常用解法.關于補形法,絕大多數文章都只是列舉幾種常用的可以補成長方體的四面體,普遍存在類型不全、歸類不準確、重復等問題,而且沒有給出嚴格的數學證明.那么,到底什么樣的四面體能夠補成長方體呢?

類型一“墻角”四面體(過某頂點的三條棱兩兩垂直)

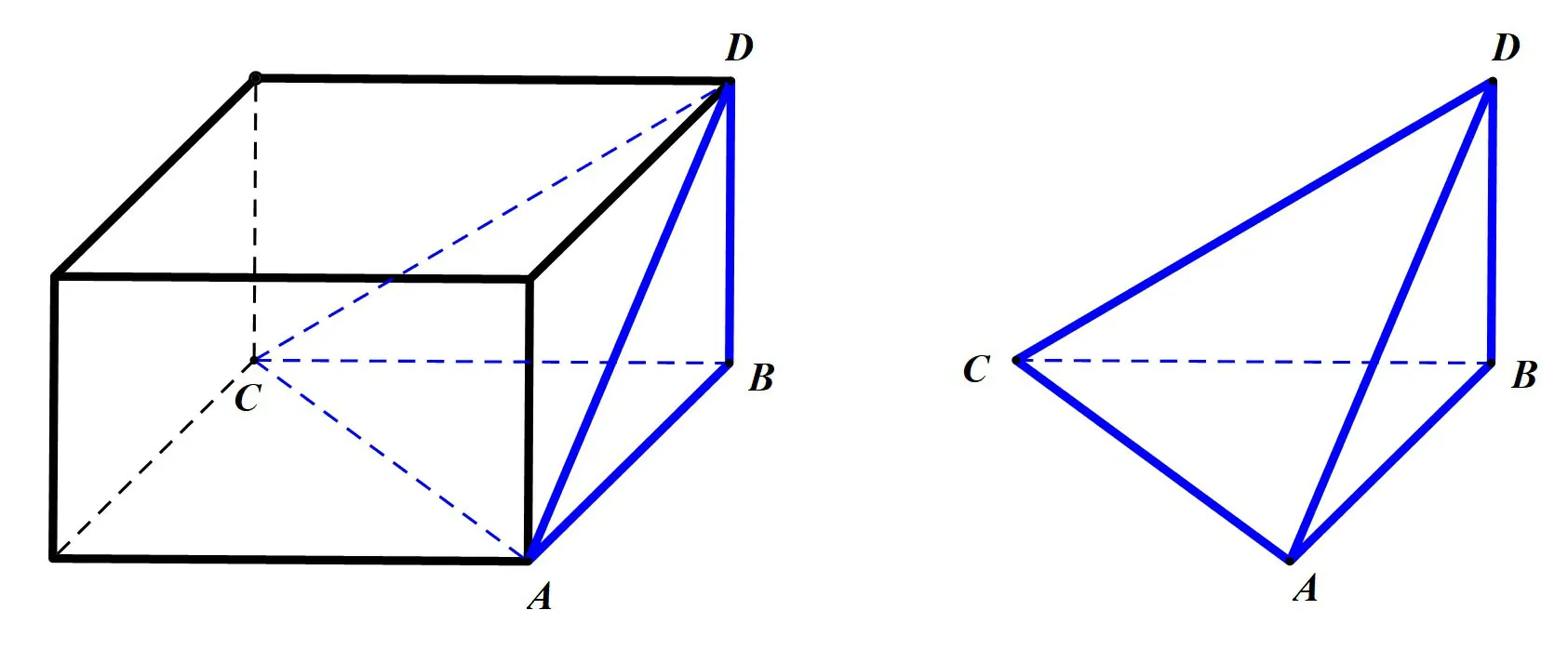
圖1

結論1過某頂點的三條棱兩兩垂直的四面體能補成長方體.

結論1 是顯然成立的.如圖1,四面體ABCD可以補成以AB、BC、BD為長、寬、高的長方體.

例1(2019年高考全國Ⅰ卷理科第12題)已知三棱錐P-ABC的四個頂點在球O的球面上,PA=PB=PC,ΔABC是邊長為2的正三角形,E,F分別是PA,AB的中點,∠CEF=90°,則球O的體積為()

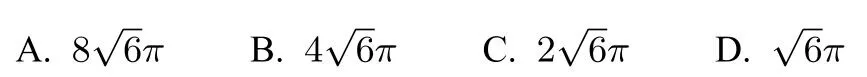
解析如圖2,因為CE ⊥EF,所以CE ⊥PB.作AC的中點G,連接PG、BG,由于PA=PC,ΔABC是正三角形,則AC ⊥PG,AC ⊥BG,從而AC ⊥平面PGB,所以AC ⊥PB.

圖2

又AC ∩CE=C且AC,CE ?平面PAC,所以PB ⊥平面PAC,則ΔPAB,ΔPAC為等腰直角三角形,得PA=PC=又AC=2,所以PA ⊥PC.從而,三棱錐P-ABC過點P的三條棱PA,PB,PC兩兩垂直,所以可以補成以PA,PB,PC為長寬高的長方體(實際上是正方體),則外接球半徑外接球的體積為

評注此題通過所給條件可以得到三棱錐P-ABC過……