對勾函數的圖像為何是雙曲線

安徽省合肥市第一中學

高中生大體上都知道反比例函數圖像是雙曲線,而且是標準形式下的等軸雙曲線逆時針旋轉45°而來,但是對其實軸長、焦距不甚了解.而對勾函數也是常見的,是其解析式形如:y=ax+(ab>0)的函數.教師常解釋其名字來源為手繪圖像酷似一對批改作業常打的“對勾”,也因像耐克商標而被稱為“耐克函數”.很多師生對這種函數存在著諸多誤解、迷惑和想當然的認識.比如,有的老師為了強調其與二次函數圖像畫法的區別,會講:對勾函數沒有對稱軸,以y軸和某條遞增的過原點直線為漸近線;有的學生會問:除y軸外的另一條漸近線方程是什么? 而部分教師也無從回答.本文用兩種方法證明對勾函數圖像也是雙曲線,并探究出其實、虛半軸長和焦距、離心率和漸近線方程等結論.

1 證明

方法 1求導得如圖1,設點(x0>0)為f(x)圖像C上的一個點,圖像C在點A處的切線為l,滿足lOA⊥l.則切線l的斜率為明顯y軸為圖像C的一條漸近線.

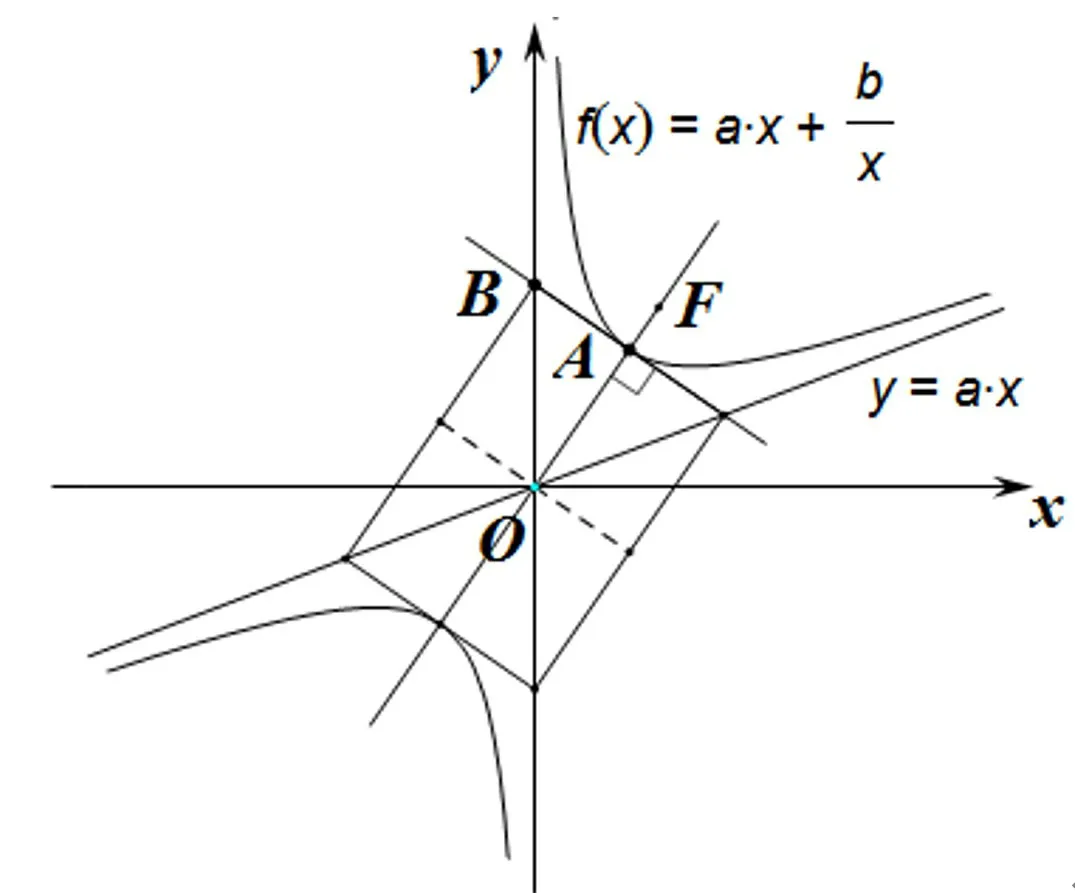
圖1

由lOA⊥l,得解得故

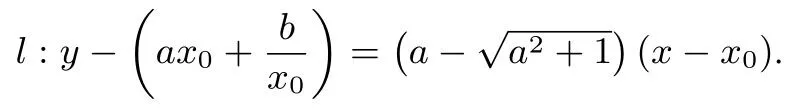
令x=0,得l與y軸交點B的縱坐標為故求得設則

另外,設點F1在射線OA上且|OF1|=c0,則故F1

設F1關于原點的對稱點為F2,f(x)圖像C上動點則

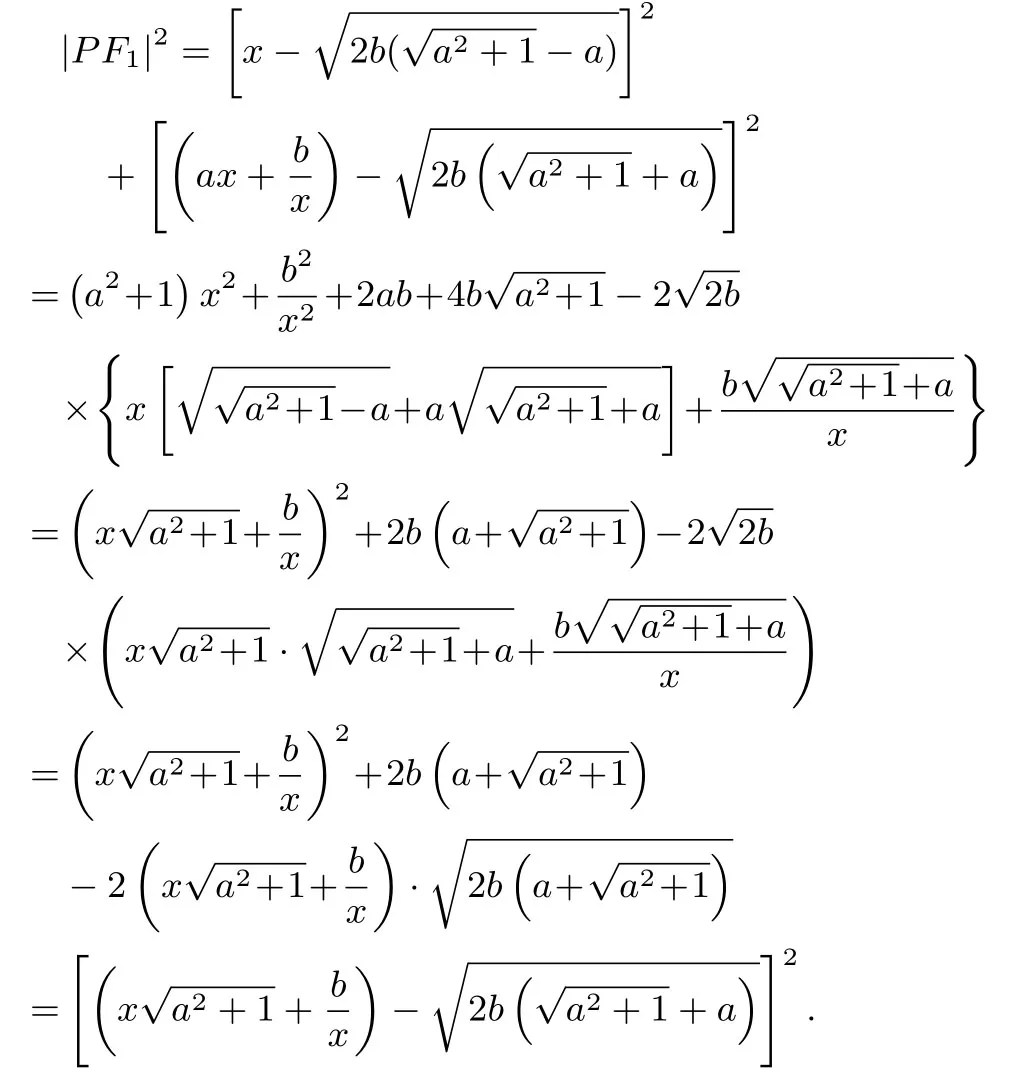
同理,

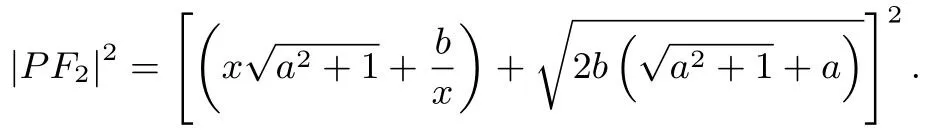
當x >0時,所以

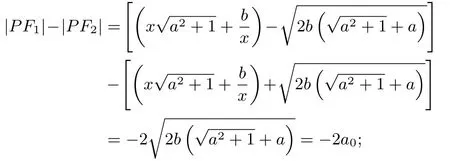
當x <0時,所以

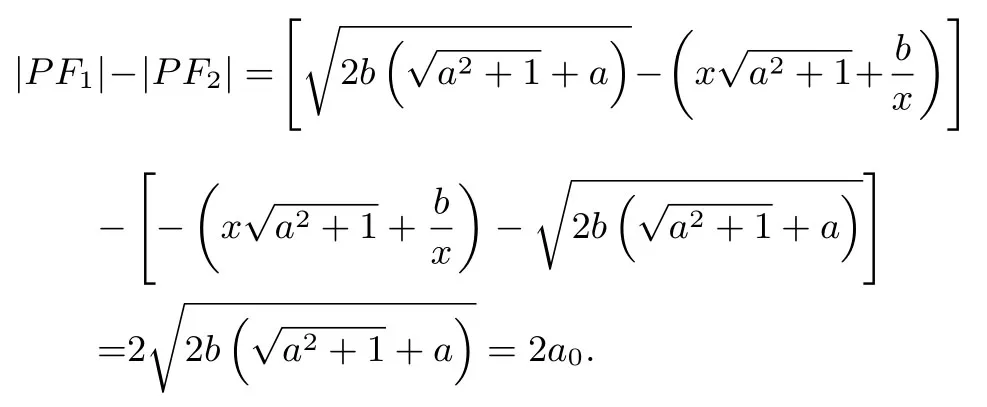
方法2設f(x)的圖像C順時針旋轉后得到曲線Γ,圖像C上任一點P(x0,y0)按此旋轉到Q(x,y).則曲線Γ 逆時針旋轉θ后得到f(x)的圖像C,將逆時針旋轉公式代入C得

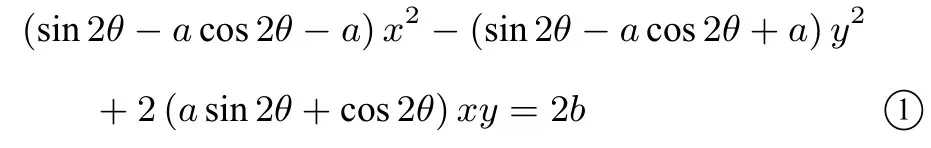
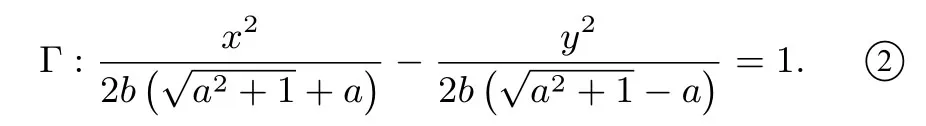
可以看出此時曲線Γ 為雙曲線,從而旋轉之前的f(x)=的圖像C也是雙曲線.

2 相關性質

2.1 推導

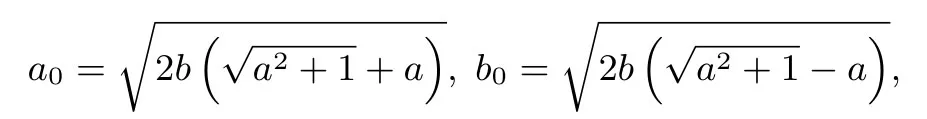
半焦距離心率而雙曲線Γ的兩條漸近線方程為:和x.l′1,l′2和x軸逆時針旋轉θ0后,即得雙曲線C……