越探究越精彩—-一道2019年高中數(shù)學(xué)聯(lián)賽題的探索

廣東省佛山市樂從中學(xué)

一 題目與解答

題目(2019年高中數(shù)學(xué)聯(lián)賽福建賽區(qū)預(yù)賽第12題)已知F為橢圓1的右焦點,點P為直線x=4 上動點,過點P作橢圓C的切線PA、PB,A、B為切點.

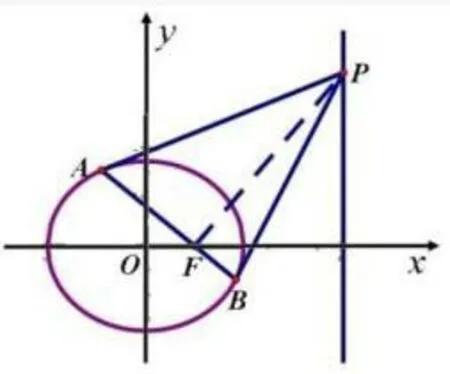
圖1

(1)求證:A、F、B三點共線;

(2)求ΔPAB面積的最小值.

解答如圖.(1)易得F(1,0),設(shè)P(4,t),A(x1,y1),B(x2,y2).則切線PA,PB的方程分別為由切線PA,PB過點P(4,t),得即由此可得直線AB方程為易知直線AB過點F(1,0).所以A、F、B三點共線.

評析問題(1)可直接用橢圓的切點弦方程求解.事實上,有如下結(jié)論:

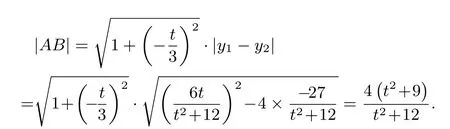
又點P(4,t)到直線AB的距離所以

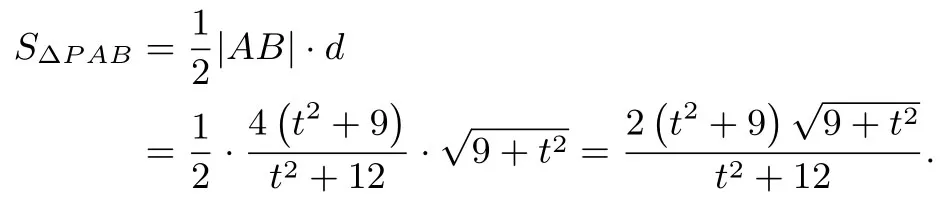
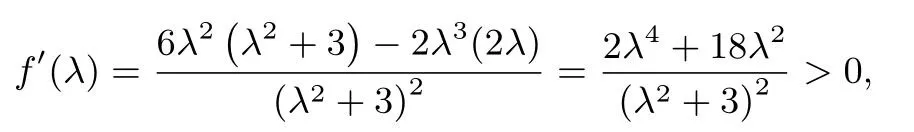
所以f(λ)在[3,+∞)上為增函數(shù),f(λ)的最小值為f(3)=此時t=0.所以ΔPAB面積的最小值為

評析問題(2)的解法是官方答案,解法的運算量雖不小,但方法是解析幾何中的常用方法,這種通性通法在數(shù)學(xué)解題中有重要作用.所以在平時的教學(xué)中要注重一般性的解題規(guī)律和方法(即通性通法),要重視知識的生成過程,盡量創(chuàng)設(shè)問題情境引導(dǎo)學(xué)生探究知識,培養(yǎng)學(xué)生分析問題、解決問題的能力.

二 問題的提出及一個引理

數(shù)學(xué)家波利亞曾說:“解題就象采蘑菇一樣,當(dāng)我們發(fā)現(xiàn)一個蘑菇時,它的周圍可能有一個蘑菇圈.”解答完本題后,自然思考:

問題1競賽題的問題(1)在一般的橢圓1(a>b>0)是否成立?

問題2若問題1 成立,則ΔPAB面積是否有最小值?如有,最小值是多少?

問題3在原競賽題的條件下,還有沒有其它性質(zhì)?

由于后面結(jié)論的證明要用到一個引理及其推論,這里先行給出.

引理已知圓錐曲線(橢圓,雙曲線,拋物線)的焦點F在x軸上,設(shè)傾斜角為α的直線l經(jīng)過點F,且與圓錐曲線交于A,B兩點,記圓錐曲線的離心率為e,則

推論……