基于KMV模型的我國商業銀行信用風險研究

陳媛媛 何雨晨 馬恩濤

一、引言及文獻綜述

1997 年的東南亞金融危機和2008 年的全球金融危機時刻警醒著人們防范金融風險的重要性和必要性（曹廷求和王可，2017）。而2017 年的全國金融工作會議以及黨的十九大，也將防范和化解系統性金融風險放在了更加重要的位置。十九大報告指出，應“健全金融監管體系，守住不發生系統性金融風險的底線”。目前，財政金融風險已經成為影響我國經濟穩定的重要因素（馬恩濤和陳媛媛，2017），商業銀行作為金融行業的最重要組成部分，其信用風險是引發金融危機和阻礙經濟增長的重要原因。我國銀行業監督管理委員會的年報顯示，銀行業金融機構的不良貸款余額和不良貸款率近幾年都呈上升趨勢，分別由2012 年的1.07 萬億元和1.56%增長到2016 年的2.2 萬億元和1.91%，不良貸款絕對額和相對額的雙雙上升必然意味著商業銀行所面臨的信用風險的加劇。特別是，隨著經濟新常態以來我國經濟發展速度放緩以及產業結構調整，我國的商業銀行信用風險加劇無疑，故如何有效預警和防范商業銀行信用風險是一個亟待解決的問題。基于此，本文將對我國主要上市銀行的信用風險進行詳細測量，找到近些年這些銀行信用風險的變化情況及波動原因，并提出控制和監管風險的政策建議。

由于西方發達國家的銀行信用體系起步較早，因此，國外學者對商業銀行信用風險做了一系列的研究。Seitz 和 Stickel（2002）指出分析和量化信用風險的方法對于銀行的平穩運行非常重要。Richard， Chijoriga 和 Kaijage（2008）研究開發了一個概念模型，用于進一步理解金融業欠發達經濟體中商業銀行（CB）的信用風險管理（CRM）系統。他們發現，CRM 系統的組成部分在欠發達經濟體中與發達經濟體中的商業銀行相比有所不同，意味著銀行運營的環境是CRM 系統成功的重要考慮因素。Konovalova（2009）認為對信用統計信息進行持續定量的分析，建立有效的風險評估模型可以成功地管理商業銀行信用風險。Andrianova 和 Barannikov（2013）指出為了更好地分析、管理和預測信用風險，銀行必須能夠量化相關的信用風險因素，對其進行分析和永久的監控。Bjom 和 Christian（2014）基于1998-2010 年美國銀行數據，對其信用風險和流動性風險從制度層面進行研究，發現兩者都能單獨影響違約概率，而在兩者共同作用下，違約概率會大幅上升，因此，要加強對信用風險和流動性風險的管理。Konovalova，Kristovska 和 Kudinska（2016）基于對借款人的因素分析，提出了一種信用風險評估模型，以控制商業銀行的貸款風險水平，減少和預防未來的信用風險，并改善銀行風險的管理。

我國對于商業銀行信用風險的研究起步較晚，但隨著經濟和金融的快速發展，國內學者對其研究也在不斷深入。馮宗憲、李祥發（2013）采用時變增強型向量自回歸（TV-FAVAR）模型對利率進行調整，并將其引發的宏觀經濟和金融市場的回饋響應與商業銀行信用風險的關聯性進行了實證研究，同時結合經濟形勢對實證結果進行了解釋和分析，揭示了宏觀經濟風險、市場風險與商業銀行信用風險存在動態關聯性，因此，在計量商業銀行信用風險暴露時不應忽視不同種類風險間的關聯性。凌江懷等（2013）基于10 家上市商業銀行的財務數據和股票交易數據檢驗KMV 模型在我國的適用性，結果表明KMV 模型計算出的預期違約頻率（EDF）與評級機構對銀行的信用評級相符。顧海峰（2014）從貸款企業的財務與非財務兩個層面設計測度信用風險的指標體系，同時運用模糊綜合評判法構建信用平穩狀態下商業銀行信用風險測度模型，并給出該模型的應用實例。結果發現：在信用平穩下，依賴專家評判及打分方式可使得模糊綜合評判法解決商業銀行信用風險測度問題更具操作便利性。尹釗等（2015）通過對我國十家房地產企業進行實證分析以剖析CM 模型、KMV 模型和CPV 模型對我國商業銀行信用風險的適用性和局限性。

隨著時間的推移，很多傳統的信用風險管理方法逐步形成了現代定量化的信用風險管理方法。目前最著名的信用風險度量模型有：1993 年穆迪評級公司基于Black，Schole & Merton 的期權定價模型而推出的KMV 模型、1997 年J.P 摩根提出的Credit Metrics 模型、1997 年瑞士信貸銀行基于保險精算提出的Credit Risk+模型以及麥肯錫公司綜合宏觀因素影響推出的 Credit Portfolio View 模型。Credit Metrics 模型的主要思想是根據信用評級機構測量的違約率和信用轉移矩陣來得出資產組合價值的變化，進而確定信用風險的大小，但是該模型沒有考慮市場風險，其違約率是根據過去年份違約率的算術平均值得來，并未考慮不同階段對各違約率的影響而賦予不同的權重。同時，該模型的信用等級變化遵循一個穩定的馬爾科夫過程是不合理的。Credit Risk+模型的核心是只針對企業的違約風險，即風險發生的概率和其發生時形成的損失，這種方法簡便且易于實現，從計算的角度來看極具優勢，但其沒有考慮到債務人資本結構變化而產生的信用降級風險，對于期權和外匯互換等非線性金融產品也不適用，因此該模型的應用受到了一定限制。Credit Portfolio View 模型認為宏觀因素如失業率、政府支出、匯率和GDP 增長率等的變化是引起信用質量改變的原因，它通過多因子模型對資產的信用風險和評級轉移進行分析，雖然該模型充分考慮到行業、國家甚至全球的經濟發展對企業的影響，但在現實中，違約率和信用評級也會受到一些微觀因素的影響，忽視了這些因素的作用會使結果有一定的偏差。相比之下，KMV 模型的優勢更加突出：第一，它采用上市公司的股票交易數據和財務數據，可對任何已上市的企業進行信用風險評估。第二，它是一種動態模型，數據隨著股價的變化而改變，可以隨時獲得各企業最新的預期違約頻率EDF，進而及時反映它們的信用狀況。第三，它具有一定的預測功能，KMV 模型將EDF 與股價聯系在一起，不僅能反映出各企業的歷史和當前狀況，還能合理預期未來的風險。

本文將在前人研究的基礎之上，采用穆迪評級公司修正的KMV 模型，通過GARCH(1,1)模型得到2012-2017 年我國16 家上市銀行的股權價值波動率，再使用Matlab 軟件計算出各銀行的資產價值及其資產價值波動率，進而得到違約點和違約距離。根據違約距離與預期違約頻率EDF 的映射關系可以獲得16 家銀行6年的理論EDF 值，以判斷我國商業銀行的信用風險情況。與已有研究相比，本文測算的銀行數目及年份較多，這些銀行的總資產規模占我國所有銀行80%以上，幾乎可以代表中國銀行業近些年的信用風險情況，同時，還根據現實數據對模型的變量進行敏感性分析，進而得出各變量的影響程度。

二、KMV模型的理論基礎

KMV 模型將企業的股權看作一種看漲期權，執行價格是企業的負債，標的物為企業資產價值。當企業的資產價值小于負債時，企業將選擇違約，否則不違約。該模型存在一定的局限性，如模型的假設條件比較嚴格，對長期債務沒有進行細致劃分，可能會使違約點與實際不符；假定利率在貸款期限內不變，忽略了利率風險；公司資本結構不變以及資產價值服從正態分布與實際情況有些出入。但很多學者也對KMV 模型在我國的適用性進行了實證分析，如程鵬、吳沖鋒（2002），楊星、張義強（2004），楊秀云等（2016）均認為該模型基本能夠識別我國上市公司的信用狀況，也具有較強的預測能力。

（一）資產價值及資產價值波動率

根據Black-Scholes-Merton 期權定價模型，企業資產價值和股權價值的關系為：

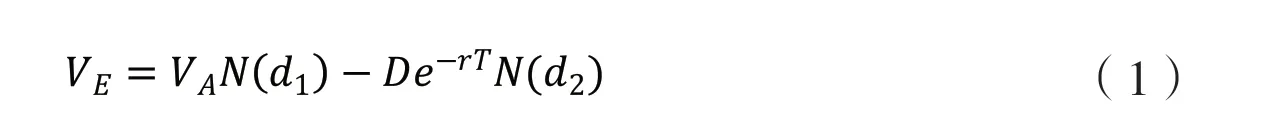
其中，

企業的股權價值波動率與資產價值波動率的關系為：

方程（1）和（2）中VE為企業的股權價值，VA為企業的資產價值，D 為企業的負債，T 為企業債務剩余期限，假設其為一年，即T=1。r為無風險利率，σA為資產價值波動率，σE為股權價值波動率，N（d）為標準正態累積分布函數。聯立兩個方程，就可得到資產價值VA及資產價值波動率σA。

（二）違約距離DD 及違約點DP

違約距離是企業的資產價值在風險期限內由當前水平降至違約點的相對距離，可以表示為：

其中，DP 為違約點，理論上來說，企業的資產價值低于負債面值總額時，就會發生違約，但是，長期負債往往能緩解企業的償債壓力，穆迪評級公司根據大量的實證檢驗，發現違約最常發生的臨界點為短期負債與長期負債的一半之和，即為公式（4），其中，STD 為短期負債，LTD 為長期負債。

（三）預期違約頻率EDF

由于假設資產價值服從標準正態分布，根據違約距離DD 的含義，理論的預期違約頻率可表示為：

由以上可知，違約距離DD 越大，上市銀行按時償還到期債務的可能性越大，信用風險越小，發生違約的概率越低，反之亦然，因此違約距離DD 和預期違約頻率EDF 呈負相關。以上為理論預期違約頻率的計算方法，穆迪評級公司根據大規模的歷史違約數據庫構建了違約距離和預期違約頻率的映射關系，從而得到經驗預期違約頻率來評估企業的信用風險。由于我國缺乏大型的企業違約數據庫，在對我國上市銀行進行信用分析時，只計算其理論的EDF 值。

三、KMV模型參數解釋與樣本數據

本文將研究2012-2017 年我國16 家上市銀行的信用風險狀況，以觀察經濟新常態以來宏觀經濟的變化對其是否造成影響。這16 家銀行包括5 家大型商業銀行，8 家股份制商業銀行以及3 家城市商業銀行。

（一）上市銀行的股權價值

這16 家上市銀行均完成了股權分置改革，不存在非流通股，因此，它們的股權價值可以表示為：

股權價值=股票收盤價×流通股股數

其中，我們采用證券市場中該銀行每個交易日的收盤價與該交易日流通股股數相乘，并進行加權平均得到其年股權價值。股票收盤價和流通股股數分別來自國泰安CSMAR 系列研究數據庫和銳思金融數據庫。

（二）上市銀行的股權價值波動率

常見的計算股票價值波動率的方法有歷史波動率法和GARCH（1，1）模型，國內學者對這兩種方法持不同意見。馮玉梅等（2016）通過實證發現GARCH 計算的動態波動率并不符合實際風險變化。張鵬等（2012）、梅建明等（2013）以及楊世偉等（2015）則認為金融時間序列常常出現某一特征值成群出現的現象，分布上表現出尖峰厚尾的特征，因此采用GARCH（1，1）模型進行計算更為合適。

1.歷史波動率法

假設上市銀行股票價格服從對數正態分布，用股票的日波動率來推算其年波動率。股票的日對數收益率可以表示為：

其中，Pi代表第i日的股票收盤價，Pi-1代表第i-1 日的股票收盤價。此時，銀行股票的日收益率的波動率為：

2.GARCH（1，1）模型

在方程（9）中，γ為對應于VL的權重，α為對應于的權重，β為對應于的權重。因為權重之和仍為1，所以有γ+α+β=1。

在估計模型的參數時，通常會采用這種形式，一旦ω、α和β被估算，我們可以由γ+α+β=1 來計算γ，長期方差VL=ω/γ。為了保證GARCH（1，1）模型的穩定，我們需要α+β＜1，否則對應于長期方差的權重會是負值。

以上可以看出，兩種方法計算出來的結果應該會存在一定的差異，我們只選取其中一個進行后續分析，GARCH（1，1）相比于歷史法更能反應實際波動率，并依據前人的經驗，最終認為GARCH（1，1）模型更為精確。

（三）無風險利率r

無風險利率采用人民銀行公布的一年期定期存款利率的加權平均值，2012-2017 年的定期存款利率分別為3.24%、3.00%、2.97%、2.12%、1.50%和1.50%，均保留兩位小數。

（四）各負債項

上市銀行的總負債D 采用其資產負債表中的負債合計值，短期負債STD 包括向中央銀行借款、同業及其它金融機構存放款項等，長期負債LTD 包括長期借款、長期遞延收益等，數據均來自銳思金融數據庫。

四、實證分析

（一）2012-2017 年我國16 家上市銀行的股權價值波動率

我們利用16 家上市銀行2012-2017 年股票的日對數收益率對GARCH（1，1）模型的參數進行估計，然后使用模型得到日收益的波動率，根據公式（8）進而得到年收益率的標準差，即股權價值波動率。

通過采用R 語言里的fGarch 包進行了模型擬合，我們得出了16 家上市銀行2012-2017 年的日收益波動率，進而得到年收益率的標準差，結果如表1 所示。

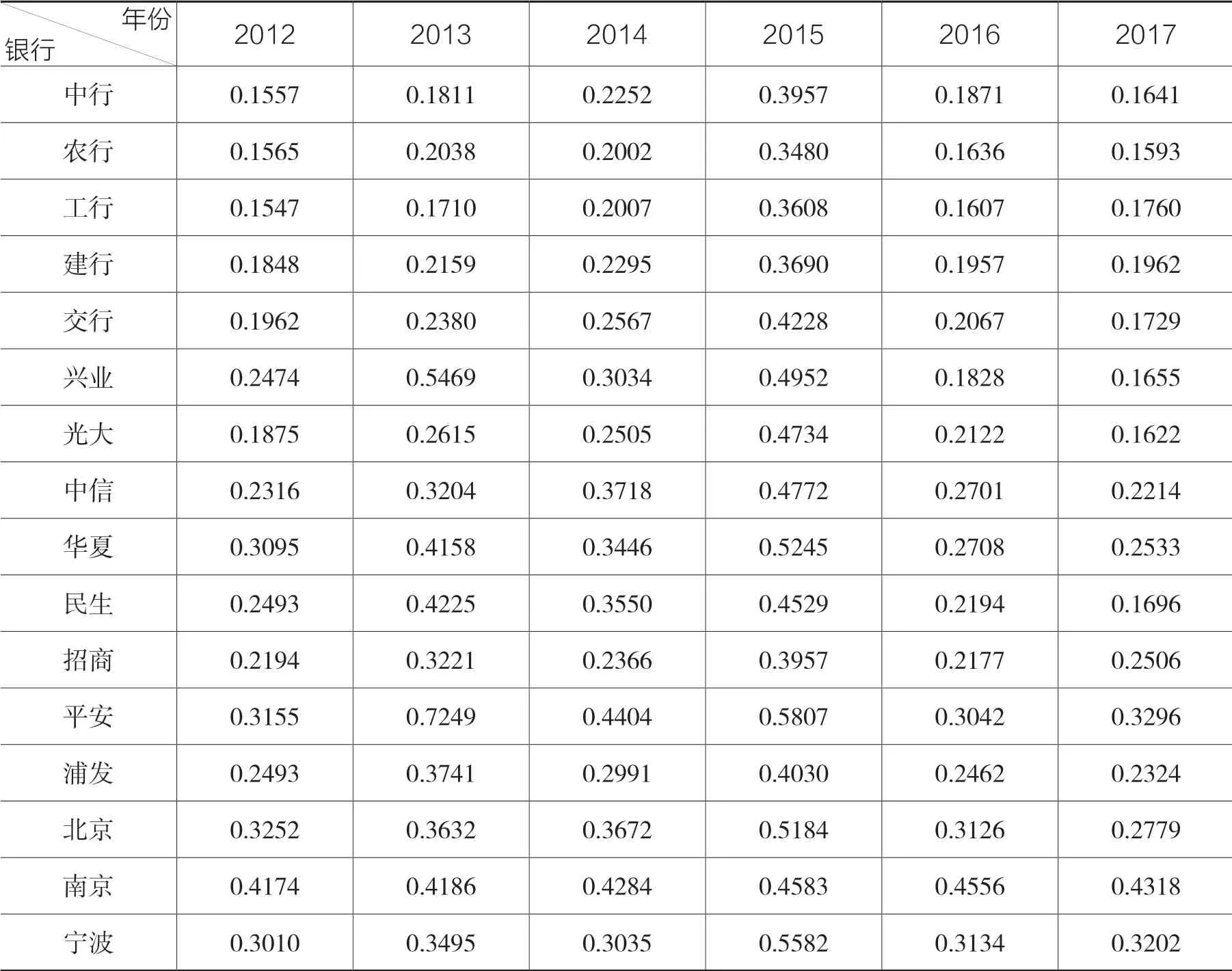
表1 16 家上市銀行的股權價值波動率（2012-2017 年）

從表1 數據，橫向總體來看16 家銀行的波動率從2012-2015 年呈現出上升趨勢，在2015 年達到峰值，2016 年和2017 兩年呈現穩定或下降的趨勢；縱向比較來看，大型商業銀行在各個年份的波動率整體上明顯低于中小型商業銀行的波動率。

（二）2012-2017 年我國16 家上市銀行的資產價值及其波動率

將GARCH(1，1)模型計算出來的股權價值波動率代入公式（1）和（2），使用Matlab 軟件得到了上市銀行的資產價值（結果保留兩位小數）及其波動率（結果保留四位小數），如表2、表3 所示。

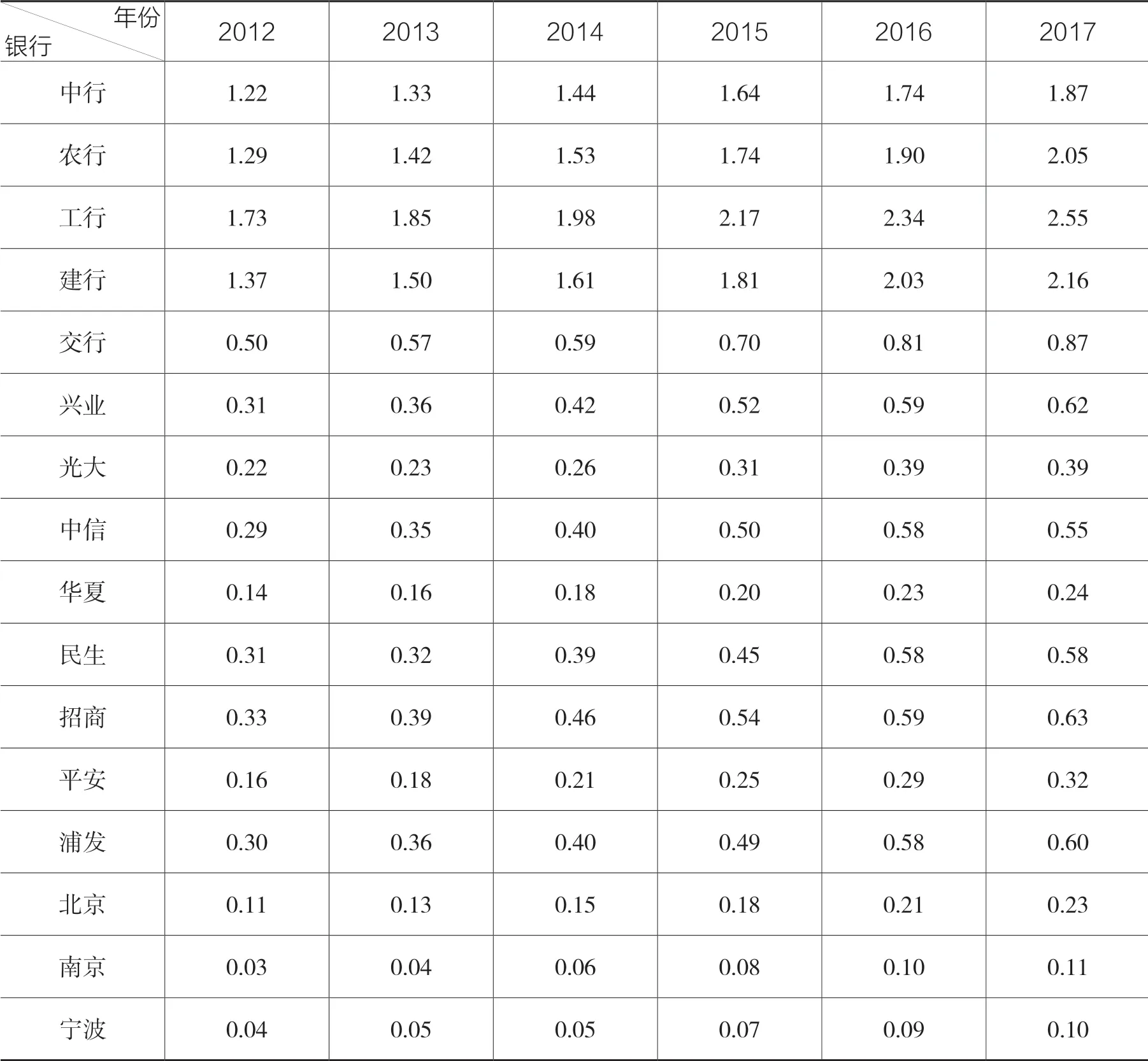
表2 16 家上市銀行的資產價值（2012-2017 年） 單位：萬億元

從表2 可以看出，每家銀行的資產價值都是逐年遞增的，以南京銀行和寧波銀行最為顯著，它們2017 年的資產價值是2012 年的三倍左右。大型商業銀行雖然增長率沒有城市商業銀行的大，但增長額也是很可觀的。

表3 16 家上市銀行的資產價值波動率 （2012-2017 年）

表3 的數據顯示，各上市銀行的資產價值波動率基本呈現先上升后下降的趨勢，在2015 年達到了最大值。

（三）2012-2017 年我國16 家上市銀行的違約距離

將GARCH（1，1）模型計算出來的資產價值及其波動率代入公式（3），使用Matlab 軟件得到了上市銀行的違約距離（結果保留四位小數），如表4 所示。

由表4 可以看出，大部分上市銀行的違約距離呈現出先減小后增大趨勢，說明它們的信用風險先增大后減小。

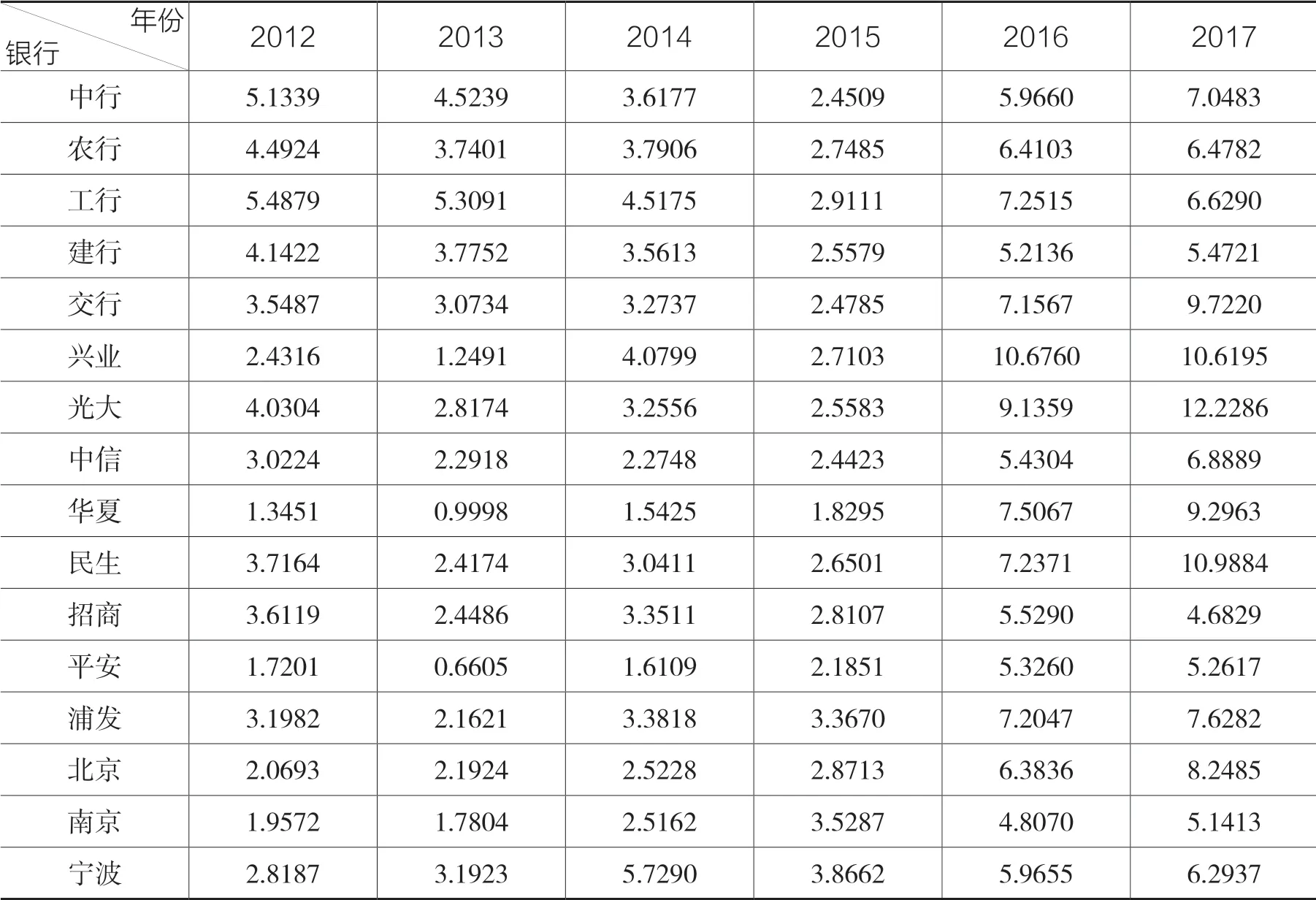
表4 16 家上市銀行的違約距離（2012-2017 年）

將這16 家上市銀行分為5 家大型商業銀行，包括中農工建交，剩下11 家為中小型商業銀行，并將GARCH（1，1）模型得到的違約距離進行加權平均進行比較。

圖1：兩類商業銀行加權平均違約距離

由圖1 可以觀察到，2012-2015 年，無論是大型商業銀行還是中小型商業銀行，其加權平均違約距離均呈下降的趨勢，2015 年以后回升，說明我國商業銀行的信用風險先增加后減少，造成這一特征的原因可能與我國經濟新常態和產業結構的調整有關。2008 年的全球金融危機和2009 年的歐洲主權債務危機席卷全球時，中國經濟在積極財政政策的調控下，以最快的速度實現了復蘇，保持了自身較高的經濟增長速度，但好景不長，2012 年中國經濟的增長速度為7.9%，首次跌到8%以下，經濟進入新常態。從2012 年開始，“四萬億”財政政策的延緩效應開始顯現，我國一些高污染高能耗行業開始出現產能過剩。以鋼鐵行業為例，國家統計局公布的粗鋼產量增長率由2012 年的5.63%下降到2015 年的-2.25%。類似這些行業的不景氣造成了無法按時償還銀行的貸款，導致銀行不良貸款率不斷攀升，從2012 年的1.56%上升到2015 年的1.94%（數據來源于中國銀行保險監督管理委員會），銀行的信用風險不斷加大。2015 年末，我國政府提出結構性改革，控制過多過度生產，實現國有企業由“量”到“質”的轉變。2016 年粗鋼產量增長率慢慢回升到0.56%，銀行的不良貸款率降到1.91%，我國商業銀行的信用風險也逐步降低，加權平均違約距離也在變大。除此之外，圖中可以看出，大型商業銀行的加權平均違約距離的波動幅度明顯小于中小型商業銀行，這說明大型商業銀行更能抵抗外界條件變化所帶來的干擾，而中小型銀行更容易受到外界沖擊的影響。

（四）2012-2017 年我國16 家上市銀行的預期違約頻率

將GARCH（1，1）模型計算出來的違約距離代入公式（5），使用Matlab 軟件得到了上市銀行的預期違約頻率，如表5 所示。

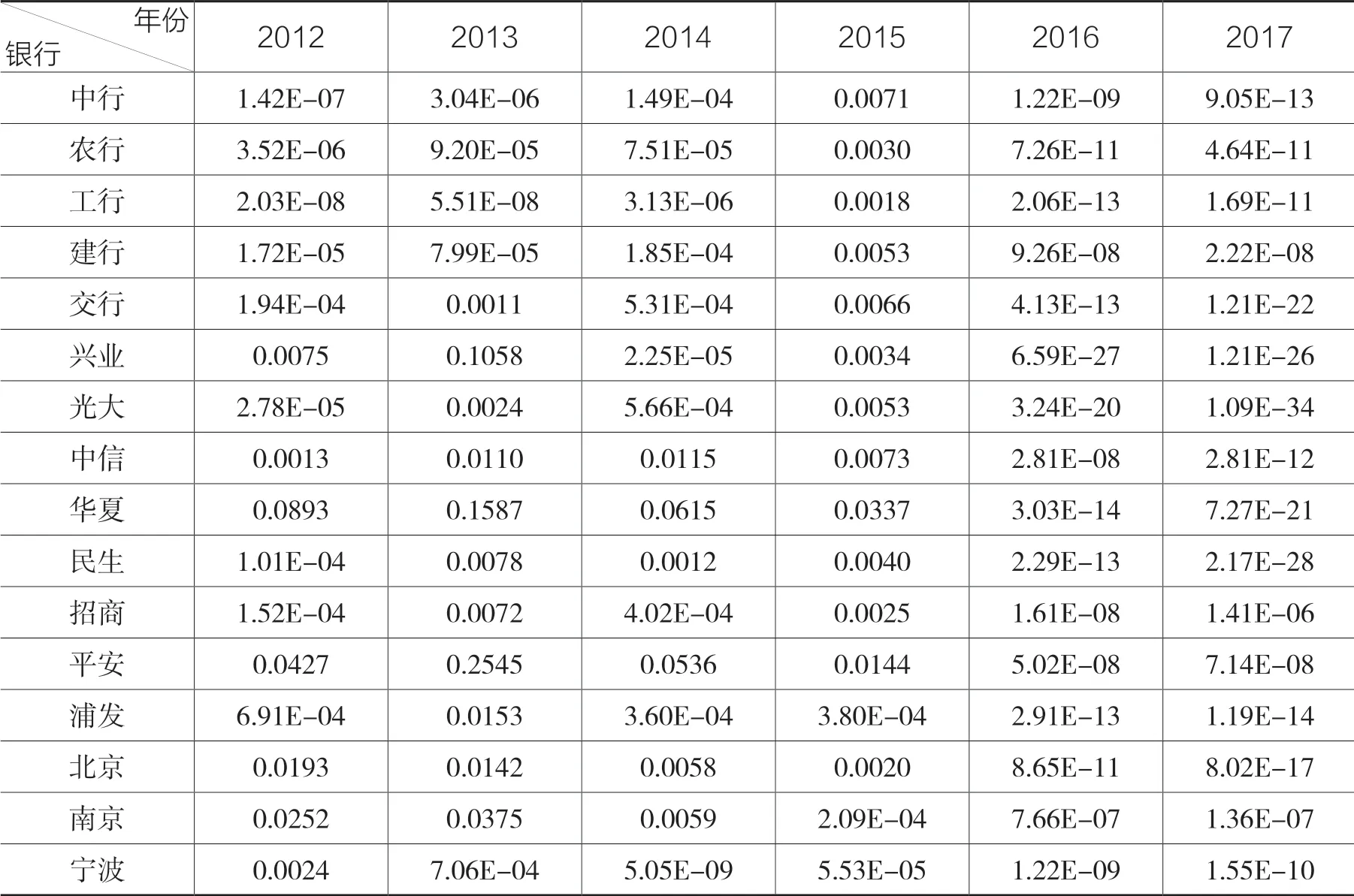
表5 16 家上市銀行的預期違約頻率（2012-2017 年）

由表5 可以得出，大部分銀行的預期違約頻率呈現出先增加后減少的趨勢，與違約距離成反比。

（五）違約距離的敏感性分析

鑒于我國還未對違約事件建立大型的數據庫，我們的預期違約頻率是根據穆迪評級公司的映射關系得出的理論值，因此，我們只對GARCH（1，1）模型計算出來的違約距離進行敏感性檢驗，以判斷16 家上市銀行的股權價值、股權價值波動率、資產價值、資產價值波動率和違約點對違約距離的敏感性。此處將使用16 家上市銀行的面板數據并采取多元逐步回歸法進行研究。

1.確定模型類型

面板數據進行回歸時常采用固定效應模型或者隨機效應模型。固定效應模型所研究的樣本為全體研究對象，在利用部分樣本數據對整體進行推斷時不太適用，而隨機效應直觀的用處就是把固定效應推廣到隨機效應，隨機效應是一個群體概念，代表了一個分布的信息或特征，依據樣本數據利用隨機效應模型來估算整體的信息。這里我們并沒有選取到所有的銀行，而是部分銀行，如果想要估算銀行業整體的特征，就應該采用隨機效應模型。同時，我們也通過檢驗來證明隨機效應模型的有效性。將違約距離、股權價值、資產價值、違約點的原始數據進行了對數化處理，對面板數據分別采用固定效應回歸模型和隨機效應隨機模型進行回歸，將得到的結果采用Stata 軟件進行霍斯曼檢驗后，發現p 值是0.8205（見表6），遠大于0.05，所以接受霍斯曼檢驗的原假設（霍斯曼檢驗的原假設是：固定效應下所估計的系數和隨機效應下所估計的系數一致，隨機效應估計的系數是最有效估計），因此模型更適用于隨機效應模型。

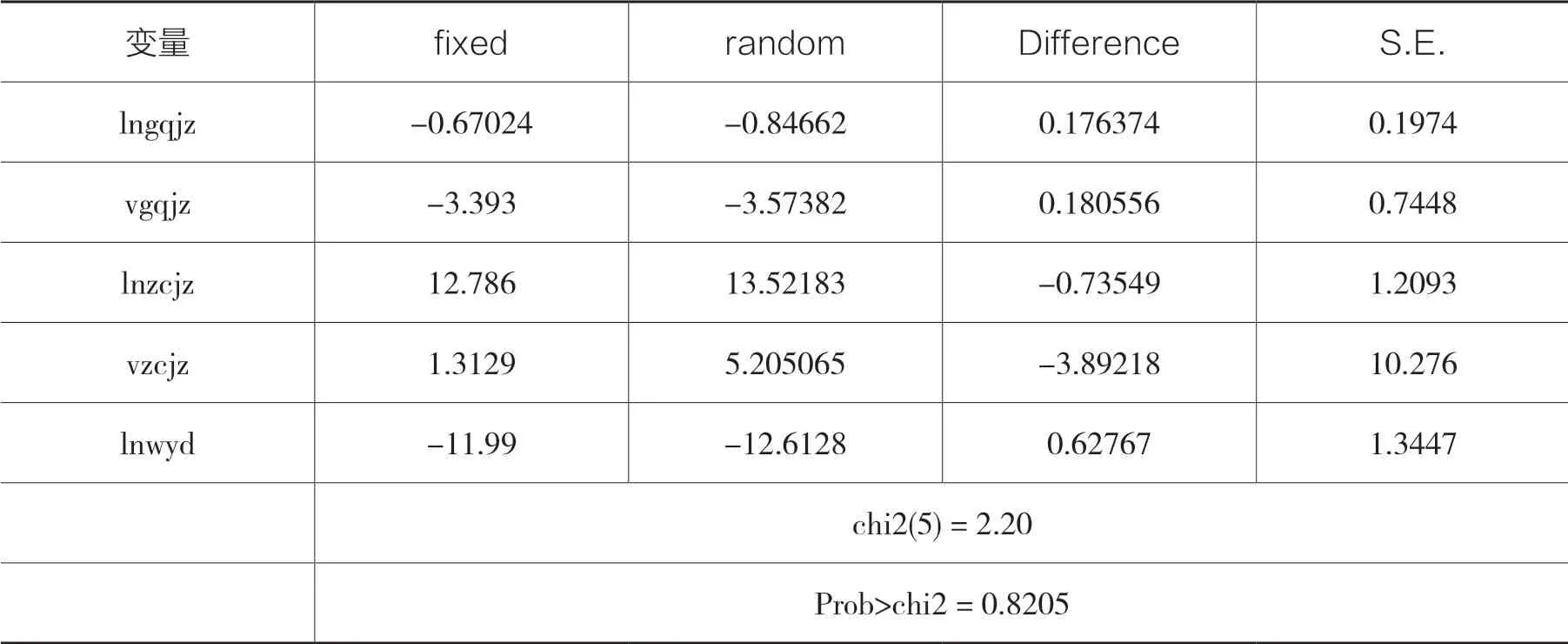
表6 霍斯曼檢驗

2.隨機效應模型回歸

將違約距離的對數看做因變量，股權價值的對數、股權價值波動率、資產價值的對數、資產價值波動率和違約點的對數看做自變量，第一次使用隨機效應模型回歸的結果如表7 所示。

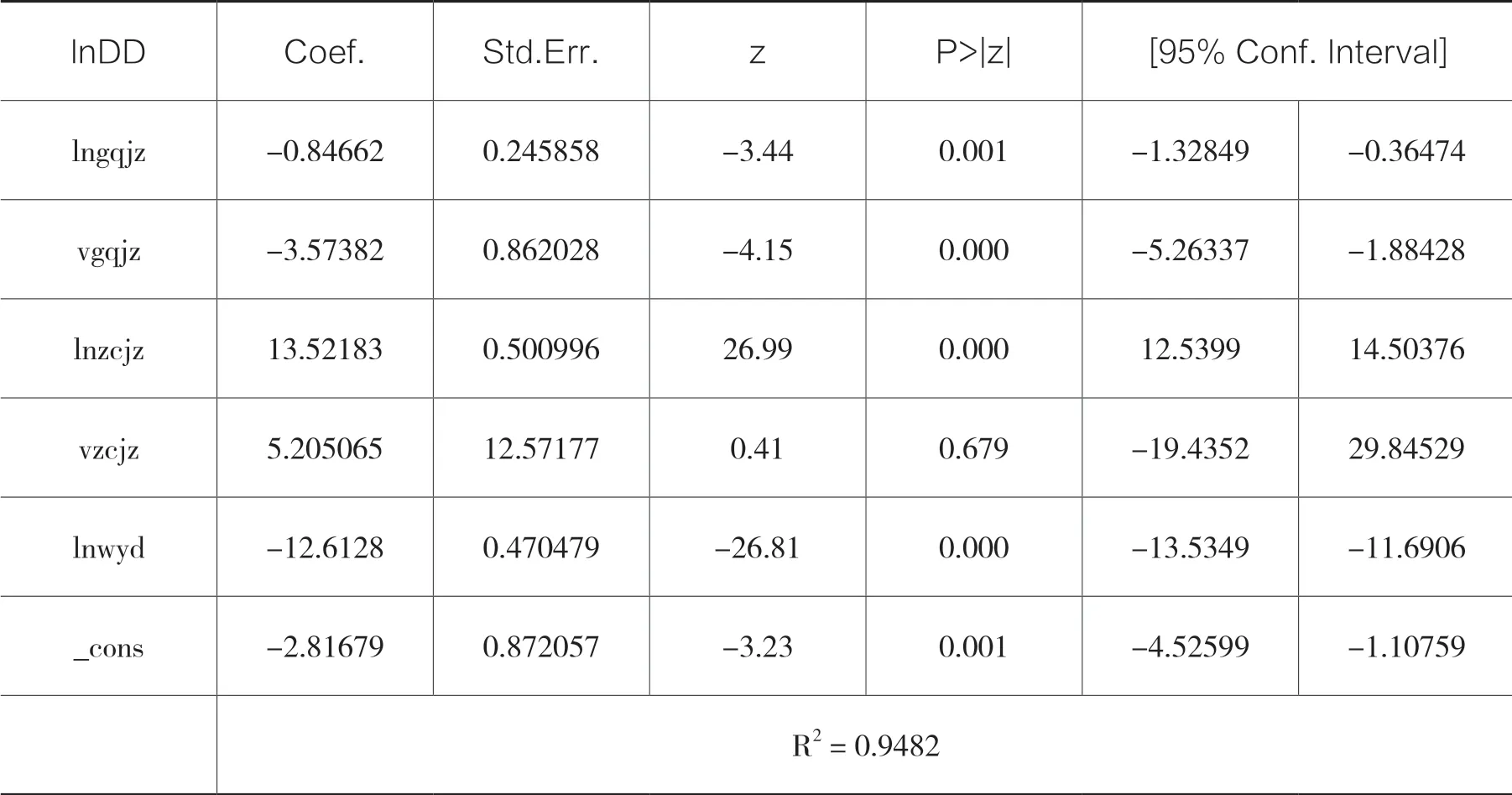
表7 隨機效應模型回歸

我們發現模型擬合優度很好，為0.9482，而在95%的置信水平下，資產價值波動率的p 值為0.679，是不顯著的，因此我們將這個解釋變量剔除，再利用隨機效應模型進行第二次回歸，結果如表8 所示。

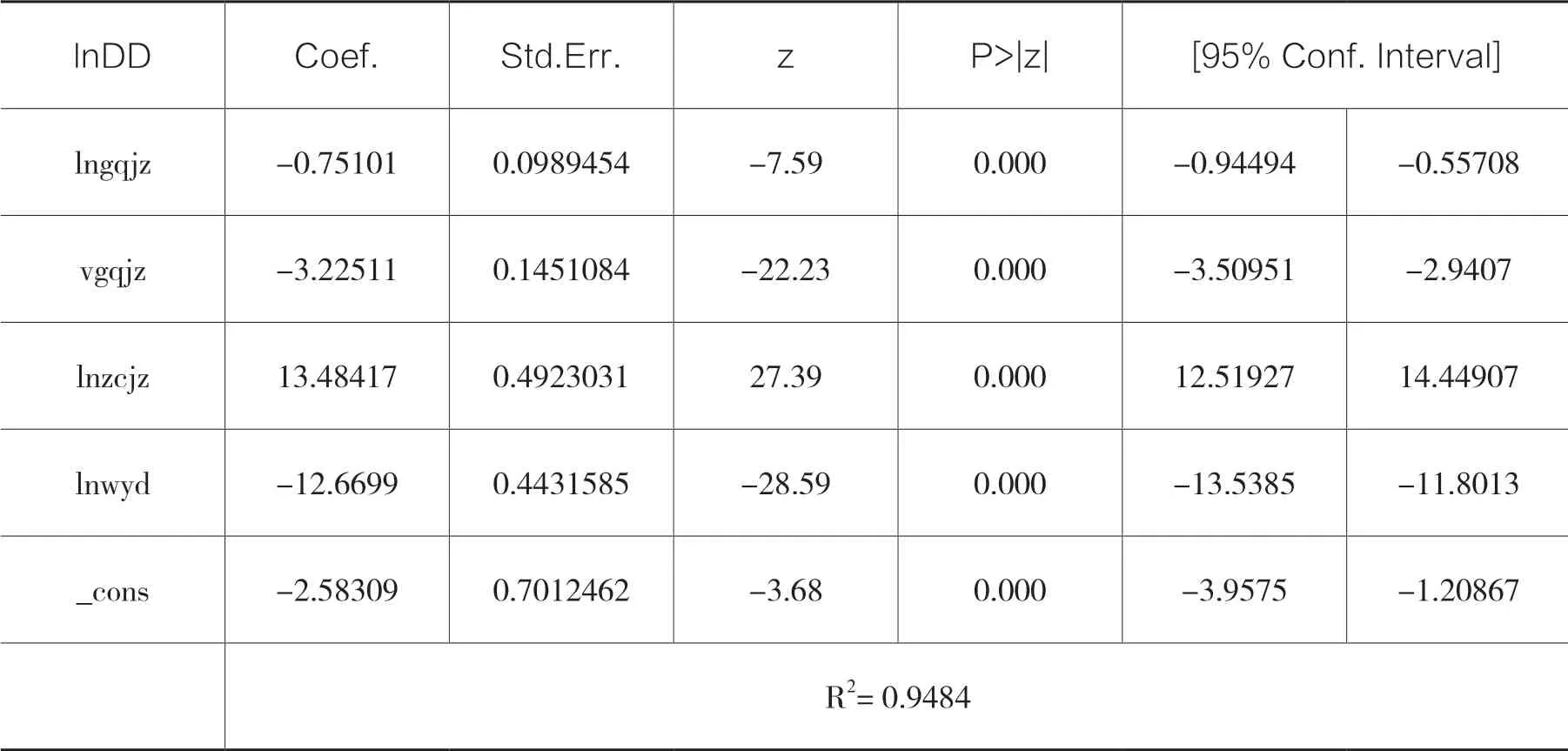
表8 剔除資產價值波動率后的回歸

模型擬合優度為0.9484，比第一次有略微提高，擬合效果很好。于是得出違約距離的估計方程為：

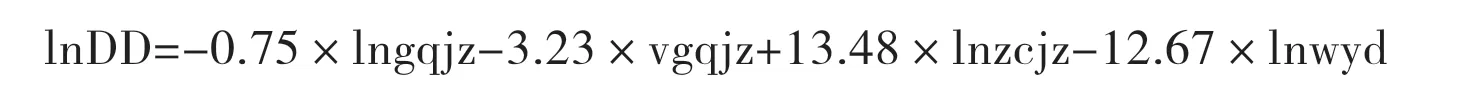
從估計結果來看：股權價值增長率增加1%，違約距離增長率減少約0.75%；股權價值波動率增加1%，違約距離增長率減少約3.2%；資產價值增長率增加1%，違約距離增長率增加約13.48%；違約點增長率增加1%，違約距離增長率減少約12.67%。很明顯，違約距離對資產價值和違約點的變化最為敏感，股權價值和股權價值波動率與違約距離均是負相關，其原因可能是我國股市受政策影響程度較大，國家在股市不景氣時往往通過提振銀行股來帶動市場，而此時實體經濟往往疲軟，銀行的風險其實是上升的。

五、結論和政策建議

本文基于KMV 模型對我國16 家上市銀行進行了信用風險研究，利用上市銀行的財務數據和估價的時間序列計算得到各銀行的違約距離和預期違約頻率，從結果中可以看出，2012-2015 年我國銀行業的信用風險呈遞增趨勢，而2015 年以來信用風險逐漸降低。其中，各銀行的資產價值以及決定違約點的銀行負債對銀行的違約距離的影響更為顯著，資產價值越大，股權價值波動率越小，信用風險越低；違約點越大即負債越多，股權價值波動率越大，信用風險越高。

通過使用KMV 模型對我國上市銀行信用風險的實證分析，整個操作過程來看，KMV 模型由于數據獲取相對容易，計算操作簡便，比較適用于我國現階段的信用風險量化管理，實用性強。但是，由于我國缺乏實際的違約距離和預期違約頻率的映射關系，該模型還不能全面應用于我國銀行業的信用風險度量。因此，為了更好的控制我國銀行業的信用風險，對其實施行之有效的監管策略，完善我國銀行業信用風險預警體系，促進其健康發展，我們給出如下政策建議：

（一）加強我國資本市場建設，完善金融經濟法律法規

政府應該建立健全相關法律法規以控制商業銀行的風險，引導各銀行提高核心資本充足率，減少不良貸款，提高應對惡性金融危機的能力，使其形成可持續發展的模式，在鼓勵金融創新的同時，更加重視風險監控和預警。此外，先進的信用風險計量模型是建立在有效的金融市場之上，KMV 模型計算過程中的大量數據來源于銀行的資產負債表及證券市場，這必然要求證券市場價格的有效性。因此，監管部門要規范各商業銀行的信息披露制度，保證其公布的信息真實有效，同時，減少證券市場的過度投機，加強交易活動的監管，使股票價格能及時可靠地反映銀行經營狀況，為KMV 模型在我國的使用提供良好的金融環境。

（二）采用國際先進的風險評估模型，完善我國信用評級體系

目前我國對銀行業的風險評估主要運用財務報表數據進行分析，具有滯后性，不能及時反映風險水平。隨著我國股票市場的日漸成熟，KMV 等先進模型越來越適合我國的國情及金融市場環境，我們應該積極學習并采用這些模型以及時反映風險變化。除此之外，進一步發展我國第三方信用評級機構也是必不可少的。目前我國的信用評級機構存在規模小、國際認可度低等問題，與權威的評級機構如穆迪、惠譽和標準普爾的操作標準存在一定差異，因此，盡快完善我國第三方信用評級機構是加強風險監控的重要組成部分。

（三）建立違約數據庫，形成我國商業銀行違約距離和預期違約頻率的映射關系

穆迪評級公司累計了15 年的違約數據建立起了違約距離和預期違約頻率之間的映射關系，該映射關系是指在一定期間以內，具有相同違約距離的公司中實際發生違約的公司數量占該違約距離的公司總數的比值，即為預期違約頻率。而我國缺乏違約數據庫，這嚴重阻礙了我國商業銀行的信用風險管理，沒有連續完整的信用違約數據也使得KMV 模型對商業銀行信用風險的測量受到了一定的限制。因此，我們必須重視數據的收集和整理，建立并逐步完善信用風險基礎數據庫，形成我國的違約距離和預期違約頻率的映射關系。

（四）加強KMV 模型的理論研究和在我國商業銀行信用風險管理中的應用

鑒于我國市場環境的特殊性，原始的KMV 模型可能并不完全適合我國上市銀行預期違約頻率的測算，我們可以對模型中的參數進行測算和修改，更好地衡量我國上市銀行的信用風險。同時，非上市銀行缺乏股價和股價波動率等數據，無法使用該模型，我們可以學習其度量思想，替換一些變量來設計出針對非上市銀行的信用風險測度模型。