基于“大概念”的“交集、并集”課堂教學設計

(江蘇省宜興中學 214200)

1 引言

《普通高中數學課程標準(2017年版)》(下稱《標準》)[1]已經頒布實行，而目前江蘇省高一、高二仍然選用上一版高中數學教材(蘇教版)進行教學．針對上述現狀，如何將核心素養“落地生根”成為一線教師最感困惑的問題．

《標準》的設計和實施追求“少而精”，雖然《標準》中并未明確數學大概念，但它將“大概念”作為課程內容框架的核心；將“大概念”作為深入理解課標議題的關鍵；將“大概念”作為孕育學科核心素養的依托．因此，“大概念”或可成為踐行數學核心素養的有力抓手．本文試圖結合課堂教學實際，從大概念的角度給出“交集、并集”的課堂教學設計，以期與大家探討．

2 “大概念”和作為大概念的“集合”

大概念，英文為Big Ideas(Big Concepts)，也有學者將其譯為大觀念[2,3]．在教育領域，有關大概念的研究至少可以追溯到布魯納對于教育過程的研究，他強調:無論教師教授哪類學科，一定要使學生理解該學科的基本結構，有助于學生解決課堂內外所遇到的各類問題．

隨著“大概念”研究的深入，“大概念”的內涵趨于統一，即“大概念”是一種高度形式化、兼具認識論與方法論意義、普適性極強的概念；它已經不再僅僅是一個簡單詞匯，它背后潛藏著一個意義的世界，它超出了一個普通概念有內涵與外延，作為一種深刻思想、學說的負載體，已成為“思想之網”的聯接樞紐．“大概念”好比“車轄”．其表述方式可以是相關的概念、主題、有爭議的結論或觀點．

作為數學學科的“大概念”，應該具備如下特點：

·大概念應當貫穿于數學課程，是最重要、最核心的數學；

·大概念應當和其他知識點具有充分的聯系；

·大概念應當體現數學的本質；

·大概念應當為今后更高層次的學習提供必要的基礎．

“集合”是全部數學的最基本概念之一，是整個數學大廈的基礎，數學的每一個分支都在使用集合論的語言進行表述與推理．因此，“集合”當之無愧成為數學學科“大概念”．

3 基于“大概念”的課堂教學設計

“集合”作為大概念，其核心在于它是數學的基本語言和工具，具有簡潔、準確和高度概括的特點．從集合的發展歷程而言，集合還推動了數學基礎研究的深入．

在高中階段，集合主要定位于語言(閱讀、表達、交流)，通過集合的學習，幫助學生用集合語言簡潔地、準確地表示相關的數學對象，發展學生用數學語言進行表達和交流的能力．內容包括：集合的概念與表示、集合的基本關系、集合的基本運算．

集合的交、并屬于運算的范疇，因此，從運算的角度理解集合的交集、并集成為本節課教學設計的中心觀點．

案例1觀察圖1所示的Venn圖，分別用陰影部分表示A∩B和A∪B．

圖1

設計理由從“形”的角度加深學生對“且”和“或”的理解,體會圖形對理解抽象概念的作用．兩個集合有且僅有如圖1所示的五種不同關系，為學生思維的后續展開提供框架和依托．

案例2(1)設A={1,2,3},B={1,3,4},C={1,5,6}，分別求A∩B,B∩A,A∪B,B∪A,(A∩B)∩C,A∩(B∩C),(A∪B)∪C,A∪(B∪C)；

(2)已知A={1,2,3,4,5,6,7,8},B={2,4,6,8}，求A∩B,A∪B；

(3)設A={x|x≤0},B={x|x≤1}，求A∩B,A∪B；

(4)設A={(x,y)|y=-4x+6},B={(x,y)|y=5x-3}，求A∩B；

(5)設A={x|x=2k-1,k∈Z},B={x|x=2k,k∈Z}，求A∩B,A∪B．

設計理由交集、并集屬于運算的范疇;數學運算是高中數學核心素養之一，主要包括:理解運算對象，掌握運算法則，探究運算思路，選擇運算方法，設計運算程序，求得運算結果．為使學生理解運算對象，在選題時特別關注運算對象的典型性和全面性，既有列舉法表示又有描述法、既有有限集又有無限集、既有數集又有點集．讓學生準確、快捷求出結果則是數學運算的基本要求，以達到“求得運算結果”的評價要求．

案例3你能從案例2的結果中發現哪些結論，你能用案例1中的圖示加以解釋嗎？你還能舉出適當的例子檢驗你的結論嗎？

設計理由讓學生觀察運算結果，鼓勵學生分類、概括，實現從具體事實向概念(原理)的跨越，通過正例和反例的辨別達到理解的目的，真正落實“為理解而教”、“為遷移而教”的教學理念．看到學生可以內化那些由事實性知識支撐的清晰而重要的概括性結論，是一件多么美妙的事情啊！本案例有效發展了學生的數學抽象素養．

本案例與交集并集的性質、蘇教版必修1第13頁練習2、習題1.3感受理解1相結合，概括出的可供參考結論清單如下：

·A∩A=A,A∪A=A；

·A∩B?A?A∪B,A∩B?B?A∪B；

·A∩?=?,A∪?=A,A∩UA=?,A∪UA=U；

·交換律：A∩B=B∩A,A∪B=B∪A；

·結合律：(A∩B)∩C=A∩(B∩C),(A∪B)∪C=A∪(B∪C)；

·A∩B=A?A?B,A∪B=A?B?A．

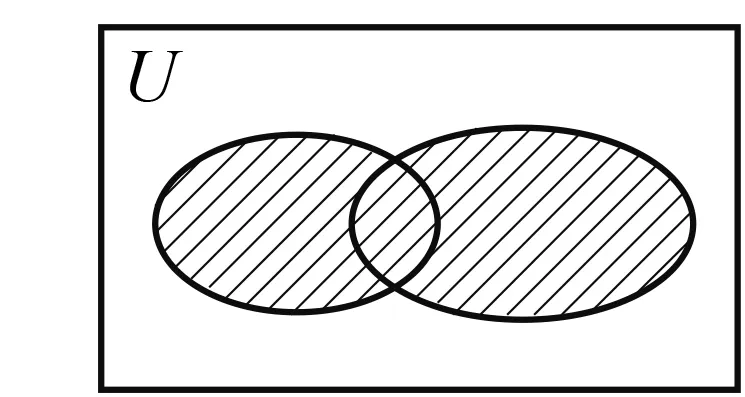
圖2

案例4(1)設U={1,2,3,4,5,6,7,8,9},A={1,2,3,5,9},B={2,3,5,7,8}，求A∩B,A∩UB,B∩UA,UA∩UB,U(A∪B)；

(2)寫出圖2中陰影部分所表示的集合；

(3)你能從上述結果中概括出一些關系嗎？你能對這些關系做出適當的解釋嗎？

設計理由為集合的交集、并集和補集創設一個綜合應用的情境，分別從“數”與“形”兩個角度相互印證，用運算律整合交集、并集和補集，以幫助學生掌握運算的法則，形成一個相對完整的集合運算系統，與學生一起獲得運算法則、認識數學結構與體系，深層次發展學生的數學抽象素養．

清晰且強有力的概括代表了學科最重要的概念性理解，讓教師感到自己的課堂極具張力，可以信馬由韁．學生可以概括出的可供參考的結論：

·(A∩B)∩(A∩UB)=?，(A∩B)∪(A∩UB)=A．

結論(A∩B)∪(A∩UB)=A除了可以用圖示法加以驗證以外，還可以通過集合運算的分配律加以驗證，其過程可以設計如下：

問題1運算律是運算得以進行的保障，請同學們想一想，對于兩個數的加法和乘法，你知道哪些運算律？

加法(乘法)交換律、加法(乘法)結合律、分配律．

問題2你能用符號表示分配律嗎？

a·(b+c)=a·b+a·c．

問題3你能類似地寫出關于交集、并集的分配律嗎？

A∪(B∩C)=(A∪B)∩(A∪C)，A∩(B∪C)=(A∩B)∪(A∩C)．

問題4你能用上述結論驗證(A∩B)∪(A∩UB)=A嗎？

(A∩B)∪(A∩UB)=A∩(B∪UB)=A∩U=A．

本設計有效發展了學生的邏輯推理素養．

案例5集合論被譽為20世紀最偉大的數學創造，創立者是德國數學家康托爾．請同學們通過書籍、網絡等方式了解康托爾的生平，查詢有關“集合論”的資料，摘錄人們對“集合”的評價，研究集合的運算律．

設計理由關注集合論的發生、發展和形成的過程，從更遠、更大、更高的視角審視高中“集合”內容．集合論的發展史能使學生們懂得對知識的敬畏；數學家康托爾生平和遭遇讓學生感受數學家的治學品質和人格魅力；人們對“集合”的評價則讓學生了解集合的價值．本案例使數學文化的滲透落到實處．

4 結語

大概念是處于學科中心位置、對學生學習具有引領作用的核心概念、法則或關系、理論或模型．大概念理念下的課堂教學由原來的基于事實的線性式教學向基于概念的整體式教學轉變．基于概念的課堂教學提供了一個不同層面心智處理的清晰描述：在事實性層面上能“知道”，在概念性層面上能“理解”，在技能和過程層面上能“做”．大概念理念的課堂教學或可成為落實數學學科核心素養的一種操作樣式．