藏“系”于身 “待定”而動
——對一道不等式證明題的分析與思考

(浙江師范大學教師教育學院 321004)

著名數學教育家G·波利亞有句名言：“發現問題比解決問題更重要.”這句話啟發我們：要想學會數學，就需要觀察，發現問題、探索問題的規律性東西要有一雙敏銳的眼睛.不等式問題一直是廣受高考和各類數學競賽青睞的考點，但是不等式中各種代數變形總是令人難以把握其精髓，尤其是一些奇思妙解，仿佛憑空而來.實際上，這并不是毫無規律可循，通過待定系數法與不等式的巧妙結合，一些復雜數學問題可迎刃而解.筆者結合自身的學習經歷，從一道不等式證明題展開分析與思考，結合各類書籍雜志中的奇思妙解和自己的一點想法，與讀者共饗.

1 試題呈現

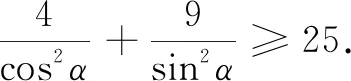
這是一道平時訓練常見的題目，主要考查的是不等式的相關知識.此題解法較多，學生的方法及花費的時間也是不盡相同.其中最常見的證法如下：

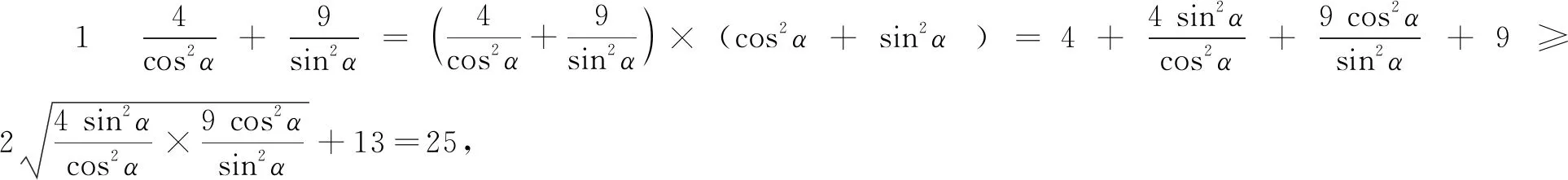
點評這是學生最容易想到的解法，也是常規解法.添“1”運用均值不等式.

筆者針對此題，有如下思考：

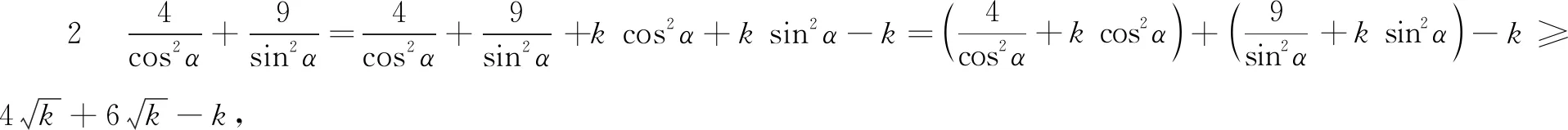
點評求解時，調整系數、拆項、補項是常用技巧.但調整系數、拆項、補項時，既要考慮不等式的結構，又要符合相關要求，難以確定.此時若使用待定系數法設k進行搭配，就可兼顧幾方面要求.第二步，運用均值不等式，只需求出系數k即可.

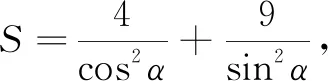
點評觀察到所給式子的分母之和為1，想到三角函數的基本公式sin2α+cos2α=1，設出系數為S，并用兩種形式表示S.與證法2頗有不同，通過運用均值不等式得出有關S的不等式，解得S范圍. 從求解方法上看，本題既落實基礎又立意新穎、不落俗套，著實是一道好題.

2 相關變式

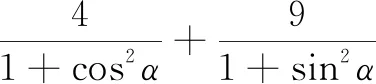
解令a=1+cos2α，b=1+sin2α，則a≥1，b≥1，于是得到

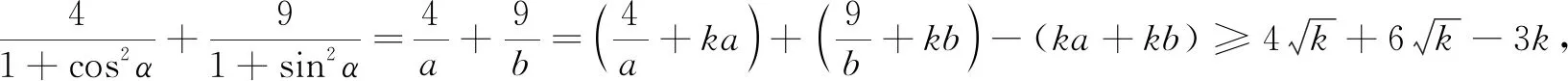
點評所給式子分母略微有點變化，但仔細一看，本質相同.只不過第一步，首先運用換元而已.第二步以及第三步與證法2完全一致.而運用證法1卻顯得繁瑣，此處體現了證法2的優勢.

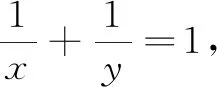
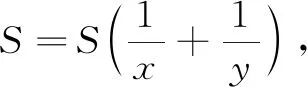
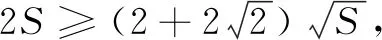
點評針對這一二元不等式的兩種證法，大部分老師或者學生都會采用證法1，往往忽略了證法2的創新.對比之下，在面對考試策略上明顯是證法1更勝一籌，但是作為平時練習，證法1忽視了解題探究中思維能力的培養，淡化了解題教學過程中學生數學學科核心素養的提升.

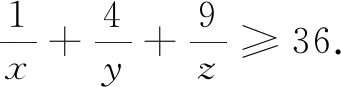
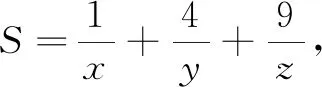
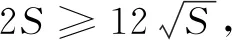
點評由二元推廣到三元，這是大部分高中生所能接受的.盡管，柯西不等式仍可以秒解，但證法2告訴我們等量的待定系數法同樣適用.

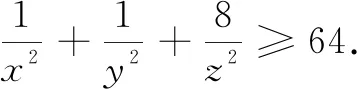
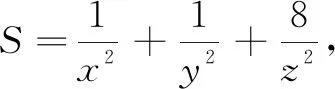
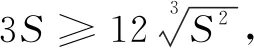
點評本題初看，難以下手，與前面幾題都有所不同，所證式子的分母次數升為2次.此時，這一類待定系數法的優勢逐漸體現出來. 設出等量，根據所求式子分母的次數，配上相應的系數，從而得證，此解法不可謂不巧.

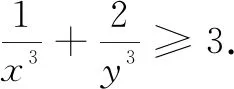
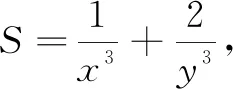
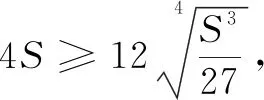
點評不難發現，在二元不等式中，所證式子分母次數變為3次，只需在等式左邊的等量配湊上系數3即可.

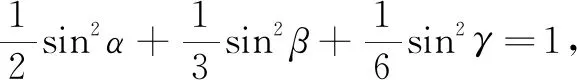
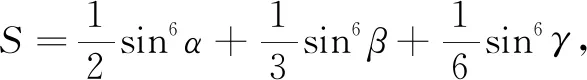
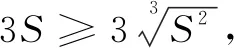
點評本題來自于數學奧林匹克叢書的一道題.從競賽的角度來說，運用赫爾德不等式可以很簡潔地證明，當然變式5同樣可以.但是其構造要求太高，學生也難以接受.而與例題相比，證法3的優勢體現得淋漓盡致.題中拓展到了三個變量，所給條件和所證式子中出現2次和6次.與證法3相同，設出等量S，根據三元均值不等式，得到有關S的不等式，得證.

3 解題反思

待定系數法是一種重要的數學方法，在許多數學問題的解決中都能看到它的“身影”.在解題時，要利用好待定系數法，首先要觀察代數式的基本模式，然后在不確定的系數位置設置參數.再結合其他條件解出參數，從而達到確定代數式的目的.待定系數法的最大好處在于不必事先知道相應系數的值，只需要用參數代替，到合適的時機再求出參數.

從本文的例題以及變式中可以窺見，待定系數法是多項式恒等變形以及求證不等式中一種有效方法，其解題步驟是：設所求為一個含有待定系數的恒等式，再根據多項式恒等的定義或者性質得到有關待定系數的不等式，求出待定系數的值，而所求即為待定系數，從而使原問題獲解.這一方面表明，數學思想方法奇妙無窮，另一方面說明，只要我們努力去探索、善于思考，將會發現任何一種數學思想方法都有用武之地.

4 結語

巧妙地運用待定系數法，設等量，恰當配湊，可以創造性地與均值不等式相結合解題.因此在教學中，需要通過各種各樣的解題方法來提高學生的思維.而每一種方法都各有利弊，我們能做到的是對每一種方法都有深刻的認識.對于教師來說，需要通過有限的典型例題學習，去理解那種解無限道題的教學機智.對于學生來說，遇到具體問題的時候，能努力地多角度思考，這樣必能尋得有趣的解法.通過這樣的探究，既開拓了學生的思路，又活躍了學生思維，培養了學生的數學能力.對于筆者而言，同樣受益無窮.