20世紀中葉以前西方早期教科書中的對數概念*

(四川省成都樹德中學 610031)

栗小妮 汪曉勤 (華東師范大學教師教育學院 200062)

1 引言

“對數”是高中數學的重點內容之一，也是聯系初等數學與高等數學的一個紐帶．德國數學家F·克萊因(F.Klein, 1849—1925)曾說：“如果希望進一步全面了解對數的理論，最好是大體上遵循其創造的歷史．”[1]眾所周知，對數是由蘇格蘭數學家納皮爾(J.Napier, 1550—1617)發明的，經過整整20年的潛心研究，他終于于1614年出版了對數著作《奇妙的對數定律說明書》．但鮮為人知的是，幾乎與此同時，另一位瑞士數學家比爾吉(J.Bürgi, 1552—1632)也獨立發明了與其非常類似的對數概念．對數大體上經歷了三個發展階段：簡化運算思想的形成、對數表的發明、對數與指數互逆關系的發現[2]，納皮爾與比爾吉的主要貢獻是開創了對數發展的第二個階段．

現行人教版高中數學教科書在“對數與對數運算”一節之后，附加了一篇閱讀材料——對數的發明，簡要介紹對數概念的歷史以及對數的應用．然而，對數概念的演進過程并不是線性的，一種新定義的誕生并非意味著舊定義的廢棄．那么，對數概念自發明以后，經歷了怎樣的演進過程？西方早期教科書或許能夠給我們提供答案．筆者通過對1700—1923年間出版的88種西方早期教科書中有關對數內容的考察(限于篇幅，大部分文獻未在參考文獻中列出)，試圖回答以下問題：早期教科書中如何定義對數？定義如何演變？對今日教科書編寫和課堂教學有何啟示？

2 研究對象

共選取20世紀中葉以前出版的88種英美早期教科書，若以50年為一段時間，則各教科書的時間分布情況如圖1所示．

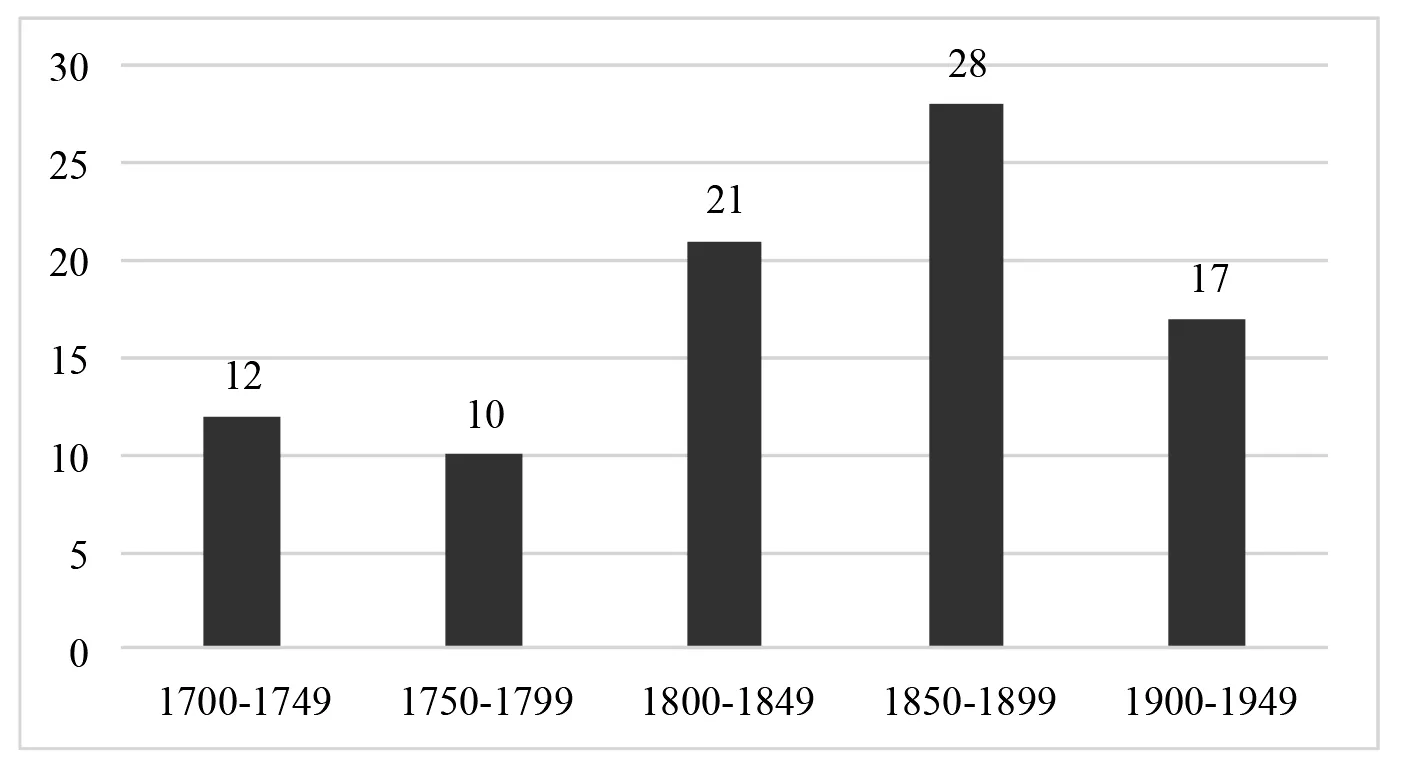
圖1 88種教科書的時間分布

查閱早期教科書發現，對數概念除了出現在代數教科書中，許多三角學著作中也花了大量篇幅介紹對數的概念、運算性質及對數表等內容，這是因為早期三角學包括平面三角和球面三角，其中涉及大量復雜的運算(如長達七位或八位數字的正弦的乘積)，當時沒有計算器、計算機等高效的計算工具，通常需要借助對數幫助人們化簡，省時又省力．

88種教科書中，有48種是代數教科書，35種是三角學教科書，2種是幾何教科書，還有3種是數學辭典或者百科全書．與今日教科書將對數編排進函數章節不同的是，在大多數早期教科書尤其是代數教科書中，對數通常單獨成章，由此可見對數在當時的重要性．

3 對數定義的分類

對比88種教科書中的對數內容發現，教科書中對數的定義不盡相同，大致可以分為四類：“雙數列定義”“比數定義”“指數定義”和“相對定義”．四類定義的具體內涵和代表著作如下．

3.1 雙數列定義

雙數列定義中構造了兩組相互對應的數列，一組為等差數列，另一組為等比數列，將等差數列中的項(又叫做“借數”(borrowed numbers)或“假數”(artificial numbers))稱為等比數列中相應項(又叫做“真數”)的對數，在總共88種教科書中占比17%．如Forster在《算術三角學》中將對數定義為“對數是構成等差數列的一組借數，與構成等比數列的另一組數相對應”．[3]這一類定義還通常與對數的運算性質一起闡述，如Ronayne在《代數專論》中給出的定義：“對數是與真數相對應的一組假數，任意兩個真數的對數(或假數)之和等于這兩個真數乘積的對數”．[4]又如Malcolm在《算術新法：理論與實踐》中這樣定義：“對數是對應于其他數而構造的數，前者的和與差對應于后者的積與商，以及冪與方根”．[5]這種定義方式較多出現于18世紀，19世紀中葉以后僅出現了一次，Whitaker在《三角學基礎》中提到“對數是一系列與普通的數相對應的數，后者的乘與除對應于前者的和與差”．[6]

結合對數的歷史可以發現，雙數列定義與納皮爾和比爾吉最初發明對數的背景最為相符，定義方式也最為相近．而我們今天教科書上對數的形式化定義早已脫離開雙數列的情形，難以從中知曉對數誕生之初的背景．

3.2 比數定義

典型的比數定義是Keill在《平面和球面三角學基礎》中給出的定義：“一個數的對數是該數與單位之間所含的比數”，[7]其后Martin(1740)、Ewing(1771)、Hutton(1785)等給出的定義都大同小異，這一定義在88種教科書中約占6.8%．與雙數列定義相似，比數定義也主要出現于18世紀，1800年后僅出現一次，這就是Wood(1825)的定義．

比數定義可能與對數的辭源有著密切的聯系．對數的英文單詞是logarithm，源于希臘文中的兩個詞logos和arithmos，分別是“比”和“數”的意思，這兩個詞組合起來就是“比數”．所謂“比數”，是指等比數列中的某一項與首項之間所含公比的個數．比如，在等比數列a,aq,aq2,aq3,aq4, …中，若要考慮aq4的對數，因為q=aq∶a=aq2∶aq=aq3∶aq2=aq4∶aq3，所以aq4與a之間含有4個公比q，即aq4的對數為4．據考察，這個“比數”很有可能就是德國數學家斯蒂菲爾(M. Stifel, 1487—1567)在《整數算術》(1544)中所說的“指數”，因為在斯蒂菲爾那個時代，還沒有明確的指數符號，他就用公比的個數來刻畫等差數列中的對應項[8]．

3.3 指數定義

指數定義是指用“冪指數”來定義對數，這一定義在88種教科書中占比最多，為75%．典型的代表是18世紀瑞士數學家歐拉(L. Euler, 1707—1783)在《無窮分析引論》(1748)中給出的對數定義：“若ax=N(a>0,a≠1)，則稱x是以a為底N的對數”，[9]這也就是我們今日教科書中所采用的對數定義．

現在人們一般認為指數定義是由歐拉首先提出來的，但值得注意的是，通過考察發現，其實在歐拉之前就已經有人開始使用指數來定義對數了，如Gardiner在《對數表》中給出的定義：“一個數的常用對數是使得以10為底的冪等于該數的冪指數的值”，[10]以及Stone在《新數學辭典》中給出的定義：“對數是某個給定數的冪指數”．[11]

或許是由于歐拉的名聲更大，他的著作對后世的影響更加深遠，所以人們一般將1748年歐拉《無窮分析引論》的出版看作是對數形式化定義的標志，也是對數概念發展過程中第三階段的開始．據統計，歐拉之后的76種教科書中有82.9%都沿用了他的定義，表明歐拉的指數定義的確對后世教科書編寫產生了重大影響，是對數發展史上的一個重要里程碑．

3.4 相對定義

相對定義是指同一代數符號在不同情境下可能有不同的名稱，需要根據某代數符號與其他不同符號或符號組合的關系而確定．這一類定義只見于英國數學家De Morgan(1835)，他在《代數學基礎》中給出這樣的定義：“在ab中，b相對于a來說是指數，但b相對于ab來說是對數，a稱為對數的底”．[12]在筆者考察的88種教科書中，相對定義僅僅出現了一次．由此可見，De Morgan的定義方式較為新穎，從代數符號的相對位置角度進行定義，關注到了代數符號本身的相對性，但其在本質上與指數定義是等價的，因此并沒有對后世產生大的影響．

4 分布與討論

4.1 分布

若以50年為分布單位，四類定義的具體分布情況如圖2所示．

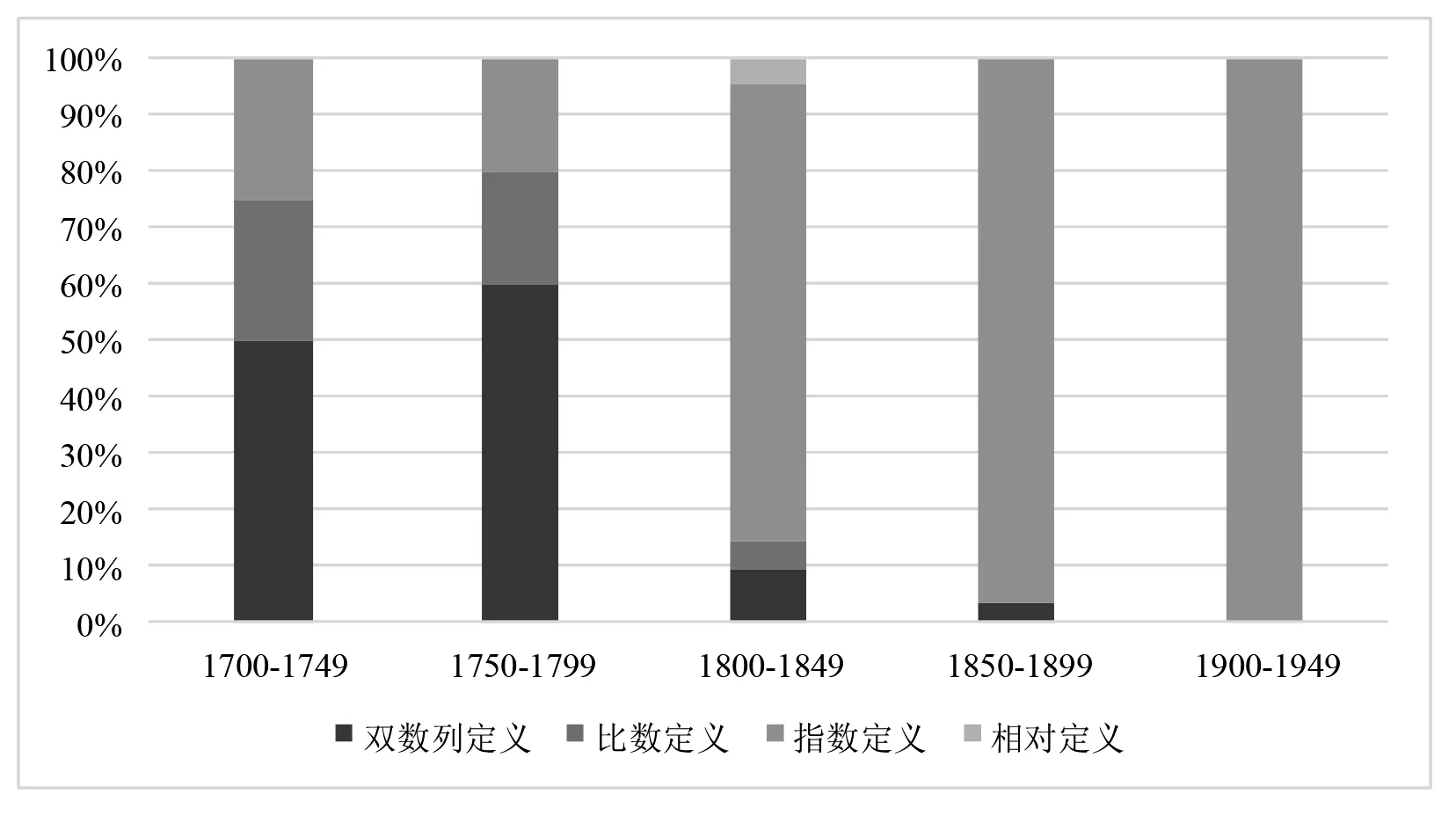
圖2 不同時期對數定義的百分比分布

從圖2中可見，從18世紀至19世紀中葉，教科書中的對數定義呈現出多樣化的特點．隨著18世紀歐拉發現指數與對數的互逆關系，此后對數的定義便漸趨統一，“雙數列定義”“比數定義”以及曾經在歷史上有過短暫亮相的“相對定義”逐漸退出歷史舞臺，“指數定義”呈現出一枝獨秀的態勢，占據了絕對的統治地位．

由于“相對定義”曇花一現，故暫且不予以考慮．圖3給出了早期教科書中所呈現的對數定義的演進過程．

4.2 與今日教科書的異同分析

早期教科書中從對數到指數的呈現順序與今日教科書中順序正好相反．早期教科書中通常是先講對數，包括對數的概念、對數的運算性質以及對數表的構造與使用，然后再講指數方程，接著對年息問題和復利問題等相關內容加以介紹．由于今日教科書都采用指數來定義對數，所以編排順序必然與早期教科書不同，這是由對數的定義方式所決定的．因此，我們可以這樣說，從教科書中指數與對數內容的編排順序可以看出那個時期數學的發展水平．

早期教科書中包含大量今日教科書不再提及的內容．早期教科書中經常出現長達幾頁的對數表，這是早期教科書的一大特征，隨著科學技術的不斷進步，對數表逐漸被更加高效實用的計算工具所替代，計算變得更加方便快捷．此外，早期教科書中還會介紹對數的“整數部分(characteristic)”和“小數部分”(mantissa)、“線性插值”“對數曲線”“對數級數”“指數方程”“余對數”(cologarithm)或“反對數”(antilogarithm)等概念，以及如何計算某個數(通常是素數)的對數值，如常用對數lg 2, lg 3, lg 5等，還有選取10作為常用對數的底數的優點等．雖然其中很多內容今天的教科書中已經不再涉及，但對數仍在許多現代數學分支中都起著至關重要的作用，利用對數函數建立數學模型有助于解決某些實際問題，對數思想具有永久的生命力，歷久而彌新，深深影響著我們的生活．

4.3 對數的早期歷史

16世紀末17世紀初，人類在天文觀測、遠距離航海、大地測量等科學領域取得前所未有的進展．這些領域與數學息息相關，涉及大量繁雜的計算，龐大的天文數字給人們(尤其是天文學家和數學家)帶來巨大的負擔，改進數字計算方法成為人們的首要目標，對數因此應運而生．對數思想主要來源于兩個方面——“指數律”(即指數的運算性質)和“加減術”(prosthaphaeresis，即三角函數中的積化和差公式)．納皮爾與比爾吉兩位數學家受此啟發，花費數十年的時間苦心鉆研，不約而同地在等差數列和等比數列相互對應的情形下，在前人以2或3作為等比數列的公比的基礎上對雙數列進行改進，分別以0.999 999 9和1.000 1為新的公比，從而構造出更加實用的雙數列(也就是龐大的對數表，標志著對數的誕生)，解決了等比數列相鄰兩項之間間隔越來越大的難題，發明了對數這一能夠降低運算級數、簡化計算的神奇工具．

部分早期教科書中提及了對數的歷史，基本停留在附加式，簡要介紹納皮爾用運動學的方法發明對數以及布里格斯(H. Briggs, 1561—1630)改進對數等相關數學史，但鮮少有教科書涉及到比爾吉用純代數的方法發明對數的這段歷史．值得一提的是，在88本教科書中有1本格外引人注目，這就是Rider(1923)的《平面三角學》，書中全面詳盡地介紹了對數的歷史．

Rider將對數作為單獨的一章，并采用重構歷史的方式進行編排．在章節的開頭展示了納皮爾的畫像，在下方簡要呈現了納皮爾的生平事跡和主要成就．第一節中介紹了指數的概念及其運算性質——兩個同底的冪相乘對應于指數相加，冪相除對應于指數相減，冪的乘方對應于指數相乘，冪的開方對應于指數相除．考慮以2為底的正整數指數冪與其指數所構成的一一對應的雙數列：

便可借助上述性質提高運算效率，但適用范圍非常有限，僅僅適用于第二行中出現的這些數，而對更多其他的2的非正整數指數冪的那些數則無法起到簡化計算的作用．因此，需要將數表擴充至更大范圍或插入其他的數(如可插入幾何中項與相應的算術中項)，體現了改進數表之需．接下來，從歷史的角度考察了對數的辭源．由于16世紀科技的發展和急劇增加的計算需求，納皮爾發明了對數，同時也提到比爾吉的對數研究工作，并詳細講述了納皮爾與布里格斯的那場曠世之約，二人相見恨晚，一言不發地對視了長達十五分鐘之久！正是這次會面，促成了常用對數的誕生[13]．

5 結論與啟示

在漫長的二百余年里，對數概念始于雙數列定義而終于指數定義．對數的歷史告訴我們，今天我們所理解的作為一個函數概念的對數，在許多方面都與它最初的構想完全不同，現代教科書中均采用指數的逆運算來定義對數，這已完全脫離了對數最初的起源，反映出隨著數學體系的不斷發展和完善，人們對對數的認識經歷了從復雜到簡單，從模糊到清晰的過程．早期教科書中對數定義從不完善到完善的過程，能夠為今日教科書編寫，尤其是以對數為主題的閱讀材料的編寫和課堂教學，帶來一定的啟示．

5.1 對教科書編寫的啟示

首先，教科書是我們傳遞文明、傳承文化的重要載體和工具，教科書中對數定義的演變過程基本反映了數學領域對數的研究過程．但一些教科書中也出現了倒退的現象，如Whitaker仍采用雙數列定義[6]．所以這就要求教科書編寫者對當前數學學科領域的發展現狀有充分的了解，才能準確把握教科書知識內容的科學性和前沿性．

其次，簡明扼要地從逆運算的角度用指數來定義對數，雖然能夠讓學生迅速掌握對數的本質，了解對數與指數的關系，對問題解決有一定的實用價值，但無助于學生理解對數學習的必要性、體會對數有什么作用，缺乏整體性理解而學到的知識很容易隨著時間的流逝而被人遺忘．雖然現行人教版教科書中有閱讀材料“對數的發明”，但并沒有說明納皮爾離散的雙數列與連續的運動模型之間到底有什么聯系、對數如何從雙數列的背景下過渡到用指數進行定義．因此，教科書編寫應體現對數定義的多樣化，揭示知識的本源、產生及發展過程．

5.2 對教學設計的啟示

歷史是課堂的參照和指南，課堂是歷史的再現與重構．教師可以借鑒對數概念的發展過程，采用重構歷史的方式整體上設計對數概念的教學，使學生感受到對數產生的自然性．歷史上對數概念的曲折發展，還可以滲透數學學科的德育價值，運用附加式，介紹對數發展過程中數學家遇到的困難，以及他們是如何克服的，讓學生了解數學并不是一蹴而就的，數學家也會遇到挫折和挑戰，幫助學生樹立數學學習自信心，養成勇敢堅強、持之以恒的精神品質．