降維突破思維難點，升維發展空間觀念

徐磊

【摘要】本文以《正方體的表面展開圖》教學為例，論述幫助學生突破學習幾何知識難點、發展空間思維的方法，建議教師通過“體—面—體”的有效轉化，用“降維”的方式讓三維立體圖“躺”下來，初步建立面體之間的聯系，再“升維”將二維平面圖“立”起來進一步認識，從而勾連學生對二維平面圖和三維立體圖之間的聯系，發展學生的空間觀念。

【關鍵詞】小學數學 幾何思維 空間觀念

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2020）45-0108-03

小學生的幾何思維具有具體性和抽象性相結合的特點，受限于自身抽象思維的發展，他們學習的幾何知識更多的是經驗幾何，而不是嚴格的以邏輯推理為公理化的體系。六年級的學生初次接觸抽象的三維立體圖形，缺少具體直觀的經驗，所以在認識和理解上往往存在很大的困難。如何幫助學生突破學習幾何知識的難點，更好地發展空間觀念呢？通過教學《正方體的表面展開圖》，筆者有了一些自己的思考與認識。

我們通過認真觀察可以發現，把立體圖形的表面展開后會有以下變化：原來存在于三維空間的6個正方形被置放到了同一平面上。原來在立體圖上最多只能同時看到3個面，而在表面展開圖上能看到正方體的6個面，把抽象化為直觀，能使正方體的特征表象更清晰，也便于學生解決一些問題。然而，這也給學生的認知帶來一些困難，如學生原本能直觀感受到在正方體上3組相對面的位置關系，而表面展開圖會因為展開的方式不同而發生變化，學生需要憑借折回的過程進行思考，這就要求學生具備一定的空間想象能力，增加了認知的難度。

在教學中，教師該如何幫助學生體會表面展開的價值，突破認知困難，發展空間觀念呢？筆者認為應從“有效”入手，做細轉化的過程，通過觀察、操作、想象等手段豐富表象，發展學生的空間觀念。具體做法如下：

一、讓“維”降下來，激發探求內需

怎樣引導學生產生把正方體的表面展開的需求呢？筆者創設了以下教學情境：

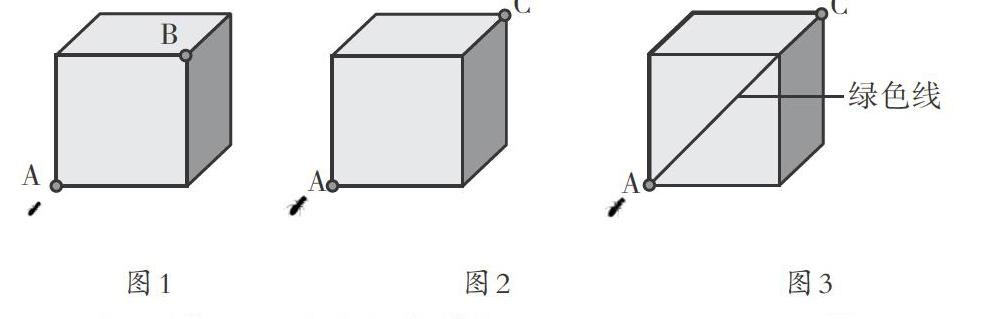
談話：小螞蟻帶來了一個正方體。從A點到B點，怎么走最近？（如圖1）你怎么想的？……是的，A、B兩點都在一個面上，同一平面內，兩點之間線段最短。

提問：如果從A點到C點，怎么走最近？（如圖2）你怎么想的？（出示學生可能規則的路線，如圖3）

圖1? ? ? ? ? 圖2? ? ? ? ?圖3

談話：從正面的A點走到上面的C點，你們都覺得綠色的路線更近，那還有沒有更近的？聯系由A點到B點的最近路線，我們得到的結論，你有沒有什么想法？同桌之間可以互相說一說。

提問：有沒有同學有新的路線？你是怎么想的？

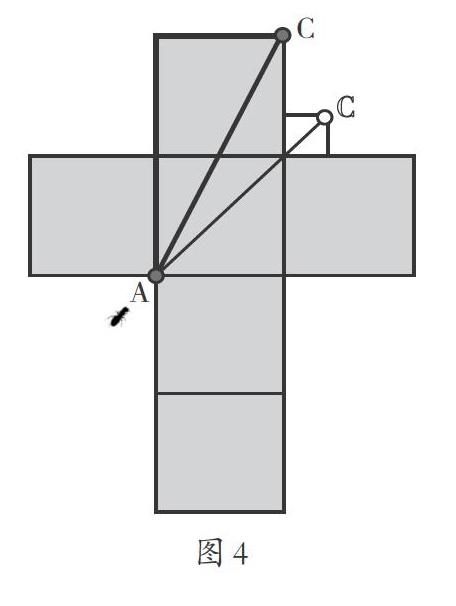
追問：他是怎么解決的？誰再來說一說。（媒體演示動態展開，如圖4）

小結：在這個正方體上，A點和C點不在同一平面，如果把正方體的表面展開，這樣A點和C點就在同一平面上了，問題就能解決了。

揭示概念，板示課題：像這樣把正方體的六個面展開放在同一平面上，并且兩兩相連，得到的圖形就是正方體的表面展開圖。本節課我們來研究正方體的表面展開圖。

從以往的教學中筆者發現，在二維圖形中學生知道“兩點之間線段最短”，而在三維立體圖上尋找不同平面內的兩點之間的最短線段，這個任務是學生根據已有經驗無法解決的，他們大多是沿著正方體的棱尋找，或將相應平面內的最短線段相連。即使學生借助實物尋找，這對學生來說依然比較抽象，他們難以找到。設計“螞蟻找最短路徑”的情境導入，一方面是借助問題情境激活學生的已有經驗，并制造新舊知識的沖突，學生會發現已有的知識經驗無法解決現有的問題，繼而自主產生學習新知的需求，從而調動學習的積極性。另一方面，通過展開正方體表面的“降維”過程，使學生發現可以將三維立體的復雜問題變成二維平面的簡單問題，初步體會到三維和二維之間的聯系，了解可以借助二維展開圖進一步認識立體圖形。

二、讓“體”“躺”下來，建立面體聯系

在認識正方體表面展開圖的環節，教材設計了讓學生沿指定路徑剪開正方體紙盒的操作活動，旨在讓學生經歷“動手剪”的過程，進而認識正方體的表面展開圖，但筆者覺得如果把教學目標僅僅停留在這一層次，不能很好地發展學生的空間觀念。

怎樣讓“體”“躺”下來呢？根據小學生的幾何思維特征，筆者認為應通過正方體“躺”下來的過程，請學生思考：剪開一個面最多需要剪開幾條棱？同一個面，剪開的棱不同，展開的方式也會怎樣？剪開不同的棱，可能會展開怎樣的面？基于這樣的思考，筆者細化了表面展開的過程：

（一）指導示范

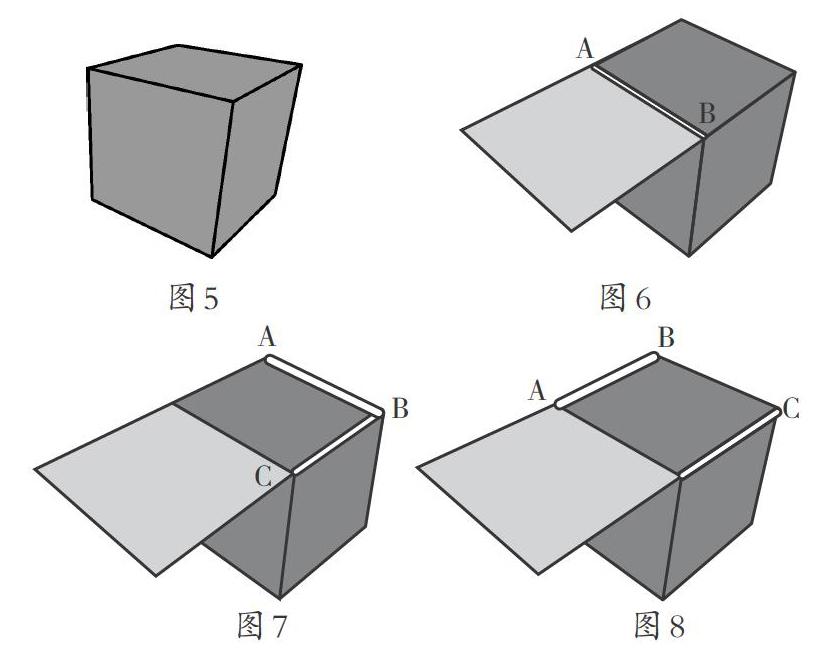
談話：正方體的表面怎么展開呢？（出示三視圖，如圖5）

1.如果要展開這個正方體的前面，想一想，需要剪開哪幾條棱？（學生回答）

如果剪開了3條棱，這條黃色的棱（圖6中的AB）還能剪嗎？（如圖6）為什么？

交流明確：展開這個面，最多只能剪開3條棱。

2.接著你想展開哪個面？（學生回答）

圖5? ? ? ? ? ?圖6

圖7? ? ? ? ? 圖8

如果展開上面，要剪開哪幾條棱？

剪開這兩條棱（圖7中的AB、BC），想象一下，這個面會怎樣展開呢？把手掌想象成上面，比畫一下。（媒體演示）和你想的一樣嗎？

（教師指）如果剪開這兩條棱（圖8中的AB、CD），又會怎樣展開？（媒體演示）

哦，同一個面，剪開的棱不同，展開的情況就會不一樣。

3.想一想，剪開這條棱會展開哪個面？右面是怎樣展開的？（媒體演示展開）和你想的一樣嗎？