在合理猜想設法驗證中發展學生思維

劉蕓

摘? 要：新課程標準倡導自主發現式學習，猜想驗證是自主發現學習模式中的一個重要組成部分，在培養學生自主學習能力和發展學生思維等方面具有重要作用。文章重點闡述了猜想驗證在小學數學課堂中的運用，通過合理猜想設法驗證活動發展學生思維，提升小學生的數學學習水平。

關鍵詞：合理猜想;設法驗證

■【案例背景】

新課程標準指出：“歸納概括得到猜想和規律，并加以驗證，是創新的重要方法。”由此可見，“提出問題―合理猜想―設法驗證―得出結論”既是一種有效的教學模式，更是一種學生需要掌握的重要學習方法。讓學生在問題情境中進行大膽假設，有了合理的猜想后，再設法用各種驗證的方法驗證猜想是否正確，通過這樣的一個探究過程，得出最后的結論。作為教師，我們應該在教學中有意識地培養學生猜想和驗證的能力，通過我們不斷地研究和嘗試，探索形成學生猜想和驗證能力的模式，從小培養學生合理猜想與設法驗證的意識和能力，引領學生投入高效的探究活動中，在教學實踐中逐步發展學生的思維，提升學生的數學素養。

■【案例描述】

在教學蘇教版五年級上冊《釘子板上的多邊形》時，筆者采用的是合理猜想設法驗證式的教學模式，引導學生在自主探索中加深對知識的理解，在潛移默化中不斷發展自己的思維。

一、提出問題，引發思考

本節課一開始，筆者給學生出示一塊釘子板，讓學生猜一猜今天可能要研究什么問題，接著提出問題：“多邊形的面積可能與什么有關？”

學生大膽猜想：多邊形的面積可能和圍成的圖形里面的釘子數有關，還可能和圍成的圖形邊上的釘子數有關。

二、開展研究，揭示規律

1. 初步探究，發現規律。

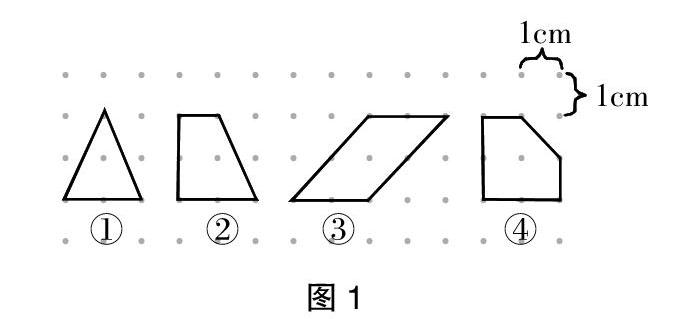
（1）出示圖片（如圖1），填寫表格。

師：請你算出這4個圖形的面積和邊上的釘子數并填寫表格。

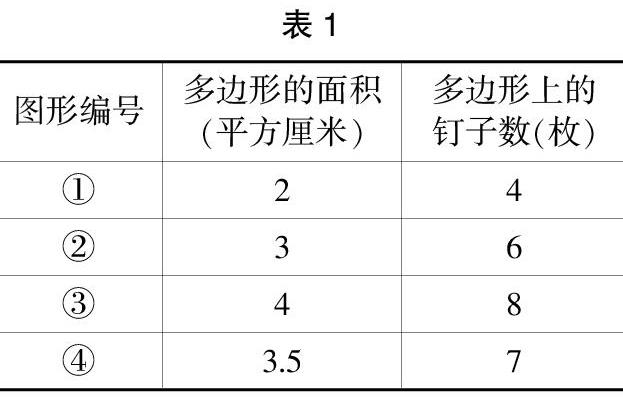
（2）觀察表格（見表1），合理猜想。

生：我發現多邊形邊上的釘子數是多邊形面積的兩倍。

師：如果用S表示多邊形的面積，n表示邊上釘子數，你能用字母簡潔地表示出它們之間的關系嗎？（S=n÷2）

（3）設法驗證，質疑反思。

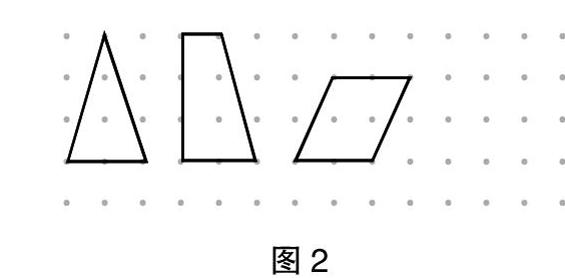
師：分別計算下面三個圖形的面積和邊上釘子數，驗證剛剛的猜想是否正確。（圖2）

（4）觀察反思，得出結論。

師：現在把兩組圖形放在一起，請你觀察比較，想一想為什么剛剛沒有驗證成功。（圖3）

生：上面一排的多邊形里面釘子數是1，下面一排的多邊形里面釘子數是2，我發現只有當多邊形里面只有一顆釘子時，S=n÷2才成立。

師：從上面幾個多邊形中我們得到了這樣的結論，那是不是只要多邊形里面有一顆釘子，就都符合S=n÷2？請你任意畫一個里面釘子數是1的多邊形，驗證這個猜想對不對。

集中交流學生驗證的結果并提問：有沒有誰的驗證是不符合S=n÷2的？

通過再次驗證且沒有找到反例，最終得出結論：當多邊形里面只有一顆釘子時，S=n÷2。

師：請你猜想，當多邊形里面有2顆釘子時，多邊形的面積和邊上釘子數有怎樣的關系？

學生猜想：S=n÷2+1。

師：請你設計一個里面有2顆釘子的多邊形，驗證你的猜想是否正確。

學生集中匯報驗證的成果，注意尋找有沒有驗證不成功的例子，在交流反饋中確認設法驗證后的結論。

2. 深入探究，完善規律。

師：請你繼續猜想，當多邊形里面有3顆釘子時，多邊形的面積和邊上釘子數又會有怎樣的關系？若多邊形里面的釘子數是4呢？是5呢？是6呢？……

出示活動要求： ①猜一猜：當里面釘子數是（? ?）時，S=（? ? ? ? ?）

②驗一驗：畫一個多邊形驗證你的猜想。

學生依次說出自己的猜想，并驗證猜想是否正確。

3. 拓展延伸，揭示規律。

（1）總結規律，得出結論。

師：通過剛才的驗證，我們發現這些猜想都是正確的。當多邊形里面釘子數就是a的時候，S=n÷2+a-1。通過今天的合理猜想和設法驗證，我們最終得出了這個結論。

（2）交流提升，應用拓展。

師：孩子們，你們知道嗎，你們今天做的事情，數學家們也在做。1899年，有一個偉大的數學家用了一種數學歸納法，證明這些結論都是正確的。播放音頻，介紹皮克定理的相關知識。

三、回顧反思，交流提升

師：本節課的最后請你說一說，我們是怎樣探究和發現規律的？你有哪些收獲？你會用今天學習的猜想驗證的方法探究事物的規律嗎？

師：回顧今天這節課，我們是先提出問題，然后進行合理猜想，設法驗證，得出結論，通過猜想驗證式的探究模式發現了數學家們也在研究的皮克定理。

■【案例反思】

本節課筆者創新教學，用猜想驗證式的學習模式貫穿始終，引導學生在多次的猜想和驗證中發現了皮克定理。回顧本節課，筆者始終在思考：如何才能讓學生的猜想合理？如何才能讓學生的驗證有效？如何才能開展高效的“猜想驗證”活動？要想解決這些問題，需要在實際教學中注意以下幾個方面的內容。

一、重視情境的有效性，激發學生的猜想欲望

本節課一開始，筆者給學生出示一塊釘子板，讓學生猜一猜今天可能要研究什么問題，接著提出問題：“多邊形的面積可能與什么有關？”學生大膽的猜想開啟了本節課的教學，通過從生活實例中抽象出數學問題，開門見山式的導入，激發了學生的好奇心和求知欲。要想激發學生合理猜想的欲望，一是要求所選的問題都對學生的猜想具有一定的啟發性和暗示性，這樣在猜想時，學生就不會做出漫無目的的猜想;二是要給學生充足的時間觀察和思考，表達自己的發現，并引導學生在發現的基礎上提出自己的猜想。

如果教師想要學生做出有一定的科學依據和針對性的猜想，那么就要重視問題情境的有效性，并且鼓勵學生先仔細觀察再提出猜想，這樣的“猜想”一定是有根有據的。在本節課中，學生通過觀察四個圖形，猜想：S=n÷2，并繼續讓學生猜想是不是所有圖形都有這個規律？怎么來驗證這個猜想呢？首先出示三個圖形讓學生驗證猜想是否正確，當學生產生認知沖突時，教師繼續引導學生在觀察比較中完善自己的猜想，接著通過舉例繼續驗證猜想的正確性。

選擇與運用恰當的情境，能夠引導學生自主參與到探索的活動中去，這對于學生興趣的激發、經驗的喚醒、數學的理解、思維的深刻等方面都起到了至關重要的作用，真正使課堂教學潛移默化、潤物無聲！

二、重視驗證的過程性，提升學生的驗證能力

如何使驗證的過程真實有效，是教學《釘子板上的多邊形》時一個值得深思的問題。

在本節課中，當學生初步感知得出S=n÷2后，筆者又出示了三個圖形讓學生驗證這個猜想是否正確，當學生產生認知沖突時，引導學生仔細觀察圖形，深入思考為什么沒有驗證成功，從而得出只有當多邊形里面僅有一顆釘子時，S=n÷2才成立。緊接著，筆者讓學生猜想當多邊形里面有2顆釘子時，多邊形的面積和邊上釘子數又有怎樣的關系。學生大膽猜想后，再自行設計一個里面有2顆釘子的多邊形，驗證猜想是否正確。接著，筆者繼續讓學生猜想當多邊形里面釘子數是3、4、5……又會有怎樣的規律，并設法一一進行驗證。通過這樣反復的猜想和嚴謹的驗證，最終得出規律：當多邊形里面釘子數是a的時候，S=n÷2+a-1。

驗證過程如果僅僅停留于表面，依樣畫葫蘆，那么僅僅只是一種“偽驗證”或“形式驗證”，起不到真正的作用。只有真正為得出結論服務的，與結論緊密結合的嚴謹的過程才是真正的驗證過程。

三、重視結論的反思性，激發學生的質疑能力

結論的驗證過程必須是科學的、嚴謹的，并且是具有一定挑戰性的。愛因斯坦曾言：“探索真理比占有真理更為可貴。”僅僅滿足于得到一個結論，那么依舊是老師“給”的，而不是自己“得”的，學生的學習能力便得不到發展。在本節課中，當學生發現S=n÷2后，筆者通過出示三個圖形讓學生驗證這個猜想是否正確，成功激起了學生的認知沖突，引導學生思考：為什么沒有驗證成功？學生在反思質疑中得出：只有當多邊形里面有一顆釘子時，S=n÷2才成立。在學生得出結論的過程中，筆者引導學生反思整個猜想驗證的過程，說一說“我們是怎樣探究和發現規律的？你會用今天學習的猜想驗證方法進行驗證嗎？”通過這一環節，讓學生感受驗證過程對得出結論的支撐作用，激發學生思考問題和解決問題時的質疑能力。

在新課程理念的影響下，數學課堂正在發生著悄然的質的變化，教學內容應具備數學思維性與數學研究的理性精神。學生學習的過程應該經歷這樣幾個步驟：提出問題―合理猜想―設法驗證―得出結論―回顧反思。作為教師，一定要踐行這樣的教學模式，讓學生在“猜想”“驗證”“歸納”到最后得出結論的過程中發展自己的思維，提升自我的數學素養，實現數學水平的大飛躍。