HPM視角下的初中數學教學

王亞美

【摘要】 勾股定理是平面幾何定理中的重要定理之一，也是中學數學教學過程中重要的一部分，它不僅是對直角三角形性質的拓展，而且為后面學習解直角三角形奠定了基礎，是把幾何問題轉化為代數問題的典范，而本文主要是探討了HPM視角下的勾股定理的教學設計，主要從勾股定理產生的背景，勾股定理證明過程中數學史的插入，以及從古至今，勾股定理的應用等幾個方面詳細闡述了數學史對于數學學習產生的影響和意義。

【關鍵詞】 數學史 勾股定理 教學設計

【中圖分類號】 G633.6

【文獻標識碼】 A

【文章編號】 1992-7711（2020）01-067-010

HPM視角下數學教學設計的主要依據之一就是發生教學法，利用發生教學法，讓所學的知識和相關的數學史聯系起來，促進學生學習數學的興趣，并提高學生理解學習的能力。數學史融入教學課堂對于學習數學具有重大的意義，數學史融入課堂分為顯性融入和隱形融入，顯性融入是指選用與本節課相關的數學史內容，直接引入課堂，在課堂教學過程中進行運用，例如本文所探討的勾股定理這節，就是明顯的顯性融入，隱性融入是指根據歷史對數學教學過程進行重新的加工和重構，使數學史融入數學課堂中。

1.勾股定理的發現與提出

勾股定理是“人類最偉大的十個科學發現之一”，是初中數學中的一個重要定理，在講授勾股定理這節課的時候，如果可以適當引入勾股定理的來源，以及與其相關的歷史，對學生的學習會有很大的幫助。

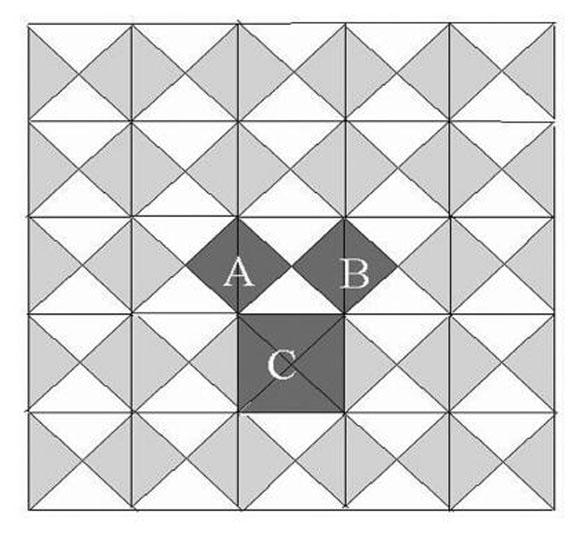
勾股定理又被稱作畢達哥拉斯定理，商高定理，百牛定理等，相傳2500年前，畢達哥拉斯有一次在朋友家做客時，發現朋友家的用磚鋪成的地面中反映了直角三角形三邊的某種數量關系，如圖所示，在這里，可以讓同學們考慮下正方形A、B、C之間的關系，這樣引入課堂會點燃學生學習的激情，會取得事半功倍的效果。很容易的發現正方形C的面積等于A的面積加B的面積，假設A的邊長為a，B的邊長是b，C的邊長是c，則發現的面積關系可以表示為a2+b2=c2.那么這是一種偶然的特殊情況還是公理呢？下面就讓同學們自己再畫幾組這樣的圖形，驗證一下這個結論的正確性。

2.勾股定理的證明

勾股定理是我們初等幾何中最重要的定理，是數形結合的重要典范，而且這個定理也有悠久的歷史，勾股定理在實際生活當中應用也十分廣泛，是數學史發展中的一大亮點，所以，兩千多年來，很多數學家對勾股定理的證明都很感興趣，上至皇帝，下至平民，都證明過勾股定理，而勾股定理常用的證明方法就有相似三角形法、面積法、鄒元志法、趙爽證法、美國總統切菲爾德證法、梅文鼎證法等，這些證法都各有優點，這既體現了數學是一門發散性思維的學科，更體現了數學文化的博大精深。因為勾股定理的證法太多，在這里，我就不一一介紹說明，在本文中，我重點通過趙爽證明法來闡釋數學史對中學數學的影響。

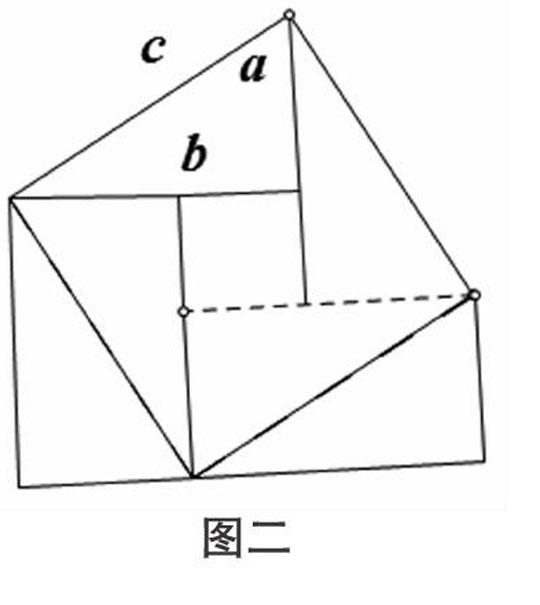
趙爽是我國三國時代的吳國人，他主要是通過創制一副“勾股圓方圖”，對勾股定理進行證明的，在這幅圖畫中，趙爽用四個全等的直角三角形圍成了一個大的正方形，而圖形中間部分是一個小的正方形，在這個圖形中，我們可以設直角三角形的兩條直角邊分別為a，b，斜邊我們可以設為是c。而這個圖形是怎么得來的呢？其實他的思路很清晰，也很容易理解，他是先構造一個由邊長為a，b的兩個正方形組成的圖形。

然后再在邊長為b的正方形上作一個直角邊分別為a和b的直角三角形，并且令這個直角三角形的斜邊為c，并連接一下，這樣就很明顯的看到形成了左右兩個直角三角形，并且很容易知道這兩個三角形是全等三角形，把這兩個三角形移動到圖（2）所示的位置，這就形成了一個邊長為C的正方形，很容易的知道，這個正方形的面積是c2，而這個圖形是由兩個正方形變化而來的，所以總面積不變，總面積又等于a2+b2，所以a2+b2=c2。

通過推理，證明了勾股定理的正確性，“勾股圓方圖”表現了我國人民對數學的鉆研的精神和聰明才智，它是我國古代數學的驕傲，所以，這個圖案也在2002年，被選為在北京召開的國際數學家大會的會徽。在課堂之余，把這些看似額外的東西告訴同學們，不僅會增強他們學習數學的興趣，而且會培養他們愛國主義情懷，除了這個證明方法外，還可以讓同學們課下搜索一下歐幾里德證法、切菲爾德證法等等，這樣既可以培養學生愛學習的能力，還可以提高他們的數學素養，而且有助于開放智力，開拓思維。

3.小結

本文只是通過中學數學中很小的一部分來介紹數學史與中學數學之間的聯系和影響，實際上數學史在中學數學中的應用非常廣泛，數學史對人類文明的進步有很大的影響，而數學史引入中學數學，對中學數學的影響也很大，首先可以通過數學史，獲取數學知識，例如本文中所講的勾股定理以及勾股定理的證明就是直接從數學史中獲得的，所以數學史是我們獲取數學知識的好途徑。然后在課堂中引入數學史不僅有利于培養學生的愛國情操，還有利于提高學生的學習興趣，增加數學的趣味性。最后，學習數學史最重要的是對學生數學思想的形成也有幫助，數學思想方法是的靈魂，只有形成掌握了思想方法，才可以提高數學成績，這對與中學學生來說，也是最實用和有意義的。

[ 參? 考? 文? 獻 ]

[1]汪曉勤：HPM視角下數學教學設計：以橢圓為例[J].數學教育學報，2011，20（5）;20-23.

[2]張永風：HPM視角下對傅立葉級數的教學設計[J].大學數學，2012，28（6）：128-133.

[5]齊黎明：勾股定理的教學設計與反思[J].中學數學，2011（4）;7-9.