恒成立問題的方法探究與建議

陳偉麗

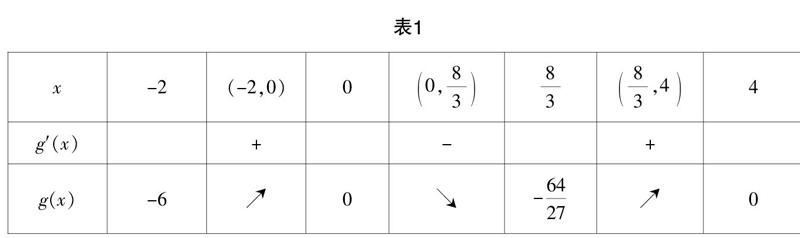
[摘? 要] 恒成立問題屬于綜合性較強的經典問題，綜合了數學的眾多核心知識、思想方法，其解法也極為靈活，對學生的解題思維要求較高. 文章結合實例講解恒成立問題的三種常用方法，并提出相應的教學建議.

[關鍵詞] 恒成立;綜合;分離變換;數形結合;差值比較

■問題綜述

恒成立問題是高中數學的典型問題，該類問題常設定在給定條件下某些結論恒定成立，進而分析關聯問題，如參數范圍、實數最值、曲線相交點. 該類問題常涉及函數、不等式、方程、圖像等知識，融合了換元、轉化、分類討論、數形結合、函數與方程等思想，對于學生的綜合解題能力有著較高的要求. 從問題的知識與思想的綜合視角分析，解析突破時主要有以下三個難點：一是問題條件隱晦，難以把握問題切入點;二是綜合性強，難以處理關聯知識;三是問題解題方法較多，難以準確選用方法來化簡. 下面結合實例簡單探討恒成立問題常用的幾種方法，構建相應的解題策略.

■方法探析

合理利用解題方法可以挖掘問題條件與結論之間的關聯，從而打開解題突破口，構建解題思路. 對于恒成立問題，常用的解法有分離變換法、數形結合法、差值比較法，下面加以探究.

解法一：分離變換法

分離變換是求解恒成立問題常用的方法之一，可用于方程、不等式有解的恒成立問題中，在實際解析時可根據研究的對象進行合理分離，如分離參數、分離整式、分離函數等. 以分離參數為例，解析時首先根據不等式或等式性質將參數分離，將問題變為一邊是參數，另一邊是變量式的形式;然后求解變量式的最值，并根據其最值來推理參數范圍或相應的結論.

例1：已知當m≤2時，不等式2x-1>m（x2-1）恒成立，試求x的取值范圍.

解析：題干所涉不等式中含有參數m，解析時可以采用分離參數的方法，只討論x2-1即可. 分析可知x2-1的符號將直接影響不等式成立的條件，因此需分三種情形加以討論，具體如下.

①當x2-1>0時，可將不等式變形為■>m，要確保不等式恒成立，只需■>2，可解得1

②當x2-1=0時，可將不等式簡化為2x-1>0，從而可解得x=1;

③當x2-1<0時，可將不等式變形為■

綜上可知，x的取值范圍為■，■.

解法點睛：上述求解不等式恒成立問題時，采用了分類討論與分離參數相結合的方式，針對數式符號來討論x的取值. 分離參數法常與其他思想方法結合起來解析問題，除了上述的分類思想外，還包括函數與方程思想.

解法二：數形結合

利用數形結合方法求解恒成立問題的核心是數形對照、數形轉換，該方法在求解函數不等式問題時有著良好的解析效果. 求解時常結合不等將其轉化為兩個函數圖像的位置關系，繪制相應的圖像曲線，然后通過函數圖像、性質分析來推導結論. 而在構建函數時需要注意一定的方法技巧，可以適度移項來構建簡潔的函數.

例2：已知f（x）=（x-2）lnx-ax+1，試回答下列問題.

（1）若f（x）在區間（1，+∞）上單調遞增，試求實數a的取值范圍;

（2）如果存在唯一的整數x■，使得f（x■）<0恒成立，試求實數a的取值范圍.

解析：（1）結合f（x）的導函數，利用函數性質即可確定a的取值. 要使f（x）在（1，+∞）上單調遞增，只需f′（x）=lnx+1-■-a≥0，即lnx+1-■≥a在（1，+∞）上恒成立. 令y=lnx+1-■，易知該函數在（1，+∞）上函數單調遞增，則只需a≤ymin即可. 當x=1時，y可取得最小值，ymin=-1，所以實數a的取值范圍為（-∞，-1].

（2）結合函數解析式可知，不等式f（x■）<0，即（x■-2）lnx■0），h（x）=ax-1，顯然g（x）的圖像為曲線，h（x）圖像為一條直線.

則g′（x）=lnx+1-■，g′（x）在（0，+∞）上單調遞增，可知g′（1）=-1<0，g′（2）=ln2>0，因此存在實數m∈（1，2），使得g′（m）=0. 當x∈（0，m）時，g′（x）<0，g（x）在（0，m）上單調遞減;當x∈（m，+∞）時，g′（x）>0，g（x）在（m，+∞）上單調遞增;所以g（x）的最小值為g（m），其中g（1）=g（2）=0.

h（x）的圖像恒過定點（0，-1），顯然a>0，圖像關系大致如圖1所示. 分析可知，若存在唯一的整數x■，使得f（x■）<0恒成立，則需kBC0，所以kAC>kDC. 因為kBC=■，所以■

解法點睛：數形結合方法最為顯著的優勢是圖像直觀，可以顯著降低思維難度. 其解法核心是移項變形、構造函數、性質解析，其中所構函數的簡易將直接影響到后續圖像繪制，而性質解析則主要利用函數的單調性、值域.

解法三：函數差值法

函數差值法的核心是作差、建函數，即對于不等式恒成立問題，可以通過移項作差的方式來構建函數，利用函數性質求解. 該方法尤其適用于f（x）>g（x）的問題，通過作差可將其轉化為f（x）-g（x）>0的形式，后續則可以據此構建新函數.

例3：已知函數f（x）=■x3-x2+x.

（1）求曲線y=f（x）的斜率為1的切線方程;