點關于直線對稱的一個新公式

胡接春

[摘? 要] 對于解析幾何中常見的點關于線對稱問題，有許多研究者給了一些直接計算的公式，如李雪松發表在《數學通訊》的《關于直線對稱點的一種求法》;張國治發表在《數學教學》的《點關于直線對稱點的簡便求法》等. 從點關于特殊直線對稱點的簡便求法出發，文章從一個全新角度思考這個陳題，得到一個新的計算公式.

[關鍵詞] 點的坐標;對稱;旋轉;矩陣變換

？搖問題1：求點P（2，3）關于直線y=x-1對稱點坐標.

方法一：設P′（x■，y■）為所求對稱點，有■=■-1，■=-1，得x■=4，y■=1，從而對稱點P′（4，1）.

方法二：x=2代入y=x-1有y=1，是對稱點縱坐標;y=3代入y=x-1有x=4，是對稱點橫坐標，故對稱點為P′（4，1）.

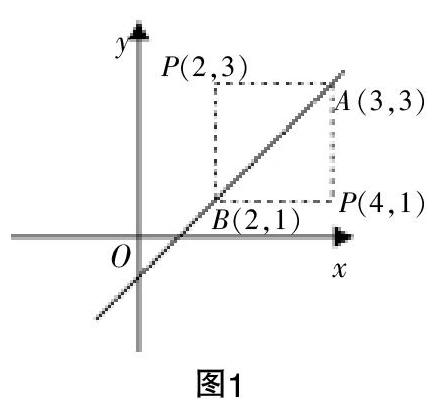
分析：方法二是將P（2，3）的橫坐標代入y=x-1得對稱點縱坐標，將P（2，3）的縱坐標代入y=x-1得對稱點橫坐標. 如圖1，四邊形PAP′B是矩形，且y=x-1恰好是對角線所在的直線. 又∠ABP′=45°，所以PAP′B是正方形，從而PP′垂直平分AB，即P與P′關于直線AB對稱.本題中，因為直線y=x-1的斜率為1，傾斜角為45°，從而能得出PAP′B是正方形，P與P′恰好對稱;類似的，當傾斜角為135°時，如，求點P（2，3）關于直線y=-x-1對稱點坐標時，用這個方法，很快得出答案P′（-4，-3）.

？搖？搖事實上，也只有求點關于斜率為±1的直線的對稱點時，能用上述快捷算法，當斜率不是±1，只能用上述方法一.筆者覺得通過坐標系旋轉，將斜率不是±1直線旋轉成新坐標系下斜率為±1的直線，然后用上述方法得到新坐標系下對稱點的坐標，再通過坐標逆旋轉成舊坐標系下的所求點的對稱點坐標.

問題2：求點P（2，3）關于直線y=3x對稱點坐標.

解：y=3x的斜率為3，令tanθ=3，我們將坐標系繞原點逆時針旋轉θ-■，由正交變換可得變換矩陣為A=cosθ-■? -sinθ-■sinθ-■? ?cosθ-■，故點P（2，3）在新坐標系下的點P■坐標為（2，3）·cosθ-■? -sinθ-■sinθ-■? ?cosθ-■，而直線y=3x在新坐標系下方程為y=x，由問題1的解答，易知對稱點P■坐標為（2，3）·-sinθ-■? cosθ-■cosθ-■? ?sinθ-■，易知，此正交變換的逆矩陣為A-1=cosθ-■? sinθ-■-sinθ-■ cosθ-■，將P■還原到舊坐標系下，得到P′坐標為（2，3）·-sinθ-■? cosθ-■cosθ-■? ?sinθ-■·cosθ-■? ?sinθ-■-sinθ-■? cosθ-■，化簡得（2，3）·cos2θ? sin2θsin2θ -cos2θ. 由tanθ=3，有cos2θ= -■，sin2θ=■，所以P′坐標為（2，3）·-■? ■■? ?■=■，■，通過用問題1中的傳統方法一驗證得，這個結果是正確的.

問題3：求點P（2，3）關于直線y=3x+5對稱點坐標.

解：直線y=3x+5的斜率為3，令tanθ=3，我們將坐標系繞原點逆時針旋轉θ-■，由正交變換可得變換矩陣為A=cosθ-■? -sinθ-■sinθ-■? ?cosθ-■，直線y=3x+5的特殊點（0，5）化為（0，5）·cosθ-■? -sinθ-■sinθ-■? ?cosθ-■=5sinθ-■，5cosθ-■，新坐標系下，直線方程為y-5cosθ-■=x-5sinθ-■，化為y=x-5sinθ-■+5cosθ-■，點P為（2，3）·cosθ-■? -sinθ-■sinθ-■? ?cosθ-■，對稱點為（2，3）·-sinθ-■? cosθ-■cosθ-■? ?sinθ-■+5sinθ-■-5cosθ-■，5cosθ-■-5sinθ-■，還原到原坐標系下（2，3）·-sinθ-■? cosθ-■cosθ-■? ?sinθ-■+5sinθ-■-5cosθ-■，5cosθ-■-5sinθ-■·cosθ-■? sinθ-■-sinθ-■ cosθ-■=（2，3）·cos2θ? ?sin2θsin2θ? -cos2θ+[-5sin2θ，5+5cos2θ]=（2，3）·-■ ■■? ■+-5×■，5-5×■=-■，■，通過用問題1中的傳統方法一驗證得，這個結果也是正確的.

下面我們來試試最一般的情況：

問題4：求點P（m，n）關于直線y=kx+b對稱點坐標.

解：y=kx+b的斜率為k，令tanθ=k，易知sin2θ=■，cos2θ=■，我們將坐標系繞原點逆時針旋轉θ-■（當θ小于■時，就繞原點順時針旋轉■-θ），類似于問題3的推導，對稱點為=（m，n）·cos2θ? sin2θsin2θ -cos2θ+[-bsin2θ，b+bcos2θ]=（m，n）·■? ■■? ■+-■，b+■=■，■=m-■，n+■，通過用問題1中的傳統方法一驗證得，這個結果也是正確的. 這個結論與《數學教學》2012年第10期的張國治的《點關于直線對稱點的簡便求法》的結果一致.

問題5：求點P（m，n）關于直線Ax+By+C=0（B≠0）的對稱點坐標.

解：由問題4，將k=-■，b=-■代入公式，得結論■

■. 這個結論與《數學通訊》2003年第6期的李雪松的《關于直線對稱點的一種求法》的結果一致.