淺談高中生主動探究能力的培養

陳奕

[摘? 要] 探究是創新的基礎，是能力發展的核心，培養學生的主動探究能力是體現新課改下“以學為本”教育理念的好方法，也是高中數學教學研究的一大熱點問題. 文章之中，研究者結合多年的教學實踐提出以下培養舉措：活用教學情境，激起探究欲望;探尋引導策略，預留探究空間;靈活變形手段，提升探究能力.

[關鍵詞] 高中數學;主動探究;策略;培養

《普通高中數學課程標準》指出：需改變學生的學習方式，由被動接受式學習轉變為主動探究式學習. 在教學實踐中，學生解決問題能力的培養得到了一線數學教師的認可和落實，而主動探究能力的培養則沒有得到足夠的重視. 基于“自主、合作、探究”這種新型學習模式，體現了新課改下“以學為本”的教學理念，并確立了新型的師生關系，角色的轉變促使當前數學教師需立足于“主動探究”這一新型模式，培養學生主動探究能力. 為此，本文結合多年的教學實踐，談談培養高中生主動探究能力的舉措，以期拋磚引玉.

■活用教學情境，激起探究欲望

培養學生的主動探究能力，首先需要培養興趣，而具有誘發性的、生動性的教學情境是調動學習積極性的有效手段. 教師要活用教學情境，創設合理而有趣、科學而生動的問題情境，將學生的思維領入相關情境之中，使他們主動去探索和研究，從而加深對新知的掌握.

案例1：以“等差數列”的概念引入為例

問題1：某校報告廳有20排座位，這個報告廳每排座位數組成了這樣一組數列：38，40，42，44，46，…你覺得這個報告廳在座位安排上有什么規律？

問題2：在統一鞋號中，每個成年女性的鞋子尺碼（以“cm”為單位）以從大到小的順序可以組成如下排列：25，24■，24，23■，23，22■，22，21■，21. 你覺得這種鞋子尺碼的排列有什么規律？

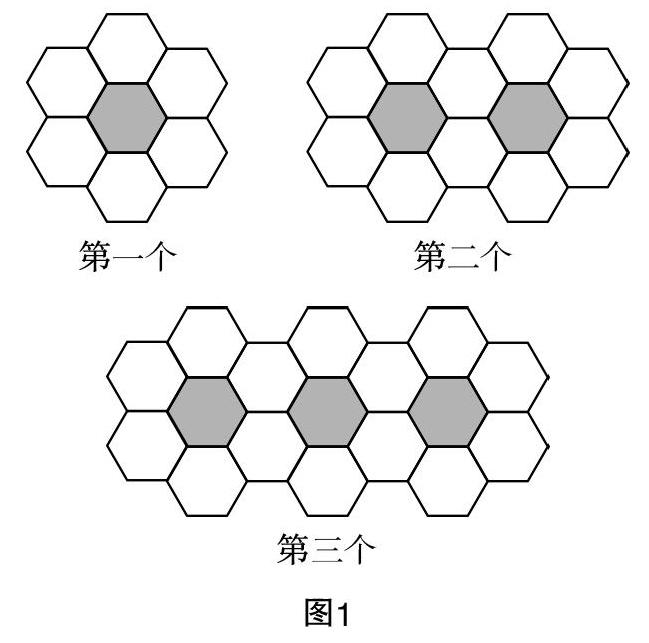
問題3：如圖1，以藍白兩色的正六邊形地磚按此規律拼圖，你知道前3幅圖中白磚的塊數依次是多少嗎？

成功的教學不是強制，也不是要求，而是一種積極主動的愿望，只有高漲的熱情才能自覺投入到探究過程中去. 以上情境中看似“紛繁”的生活場景都隱約著“等差數列”的本質，從中逐步抽象出概念并提出數學問題自然而合理，在潛移默化中激起探究的欲望，培養用數學的眼光看世界的素養. 通過學生深入觀察和實踐操作，與原有認知沖突的新問題一步步地被挖掘出來，從而激發了探求性質的創造愿望.

■探尋引導策略，預留探究空間

事實上，無論是新課的展開，或是新知的構建，又或是新技能的形成，并非是教師對學生的要求或強迫，而應是在教師的引導下，學生主動進行探索的過程. 因此，教師需探尋到引導學生探究的策略，并預留足夠的探究空間，鼓勵、激勵和誘導學生去自主探究，實現自主建構[1]. 這樣一來，不僅可以為學生的全面發展創造廣闊的空間，還可以為他們的終生發展奠定基礎.

案例2：以“離散型隨機變量的均值”的教學片段為例

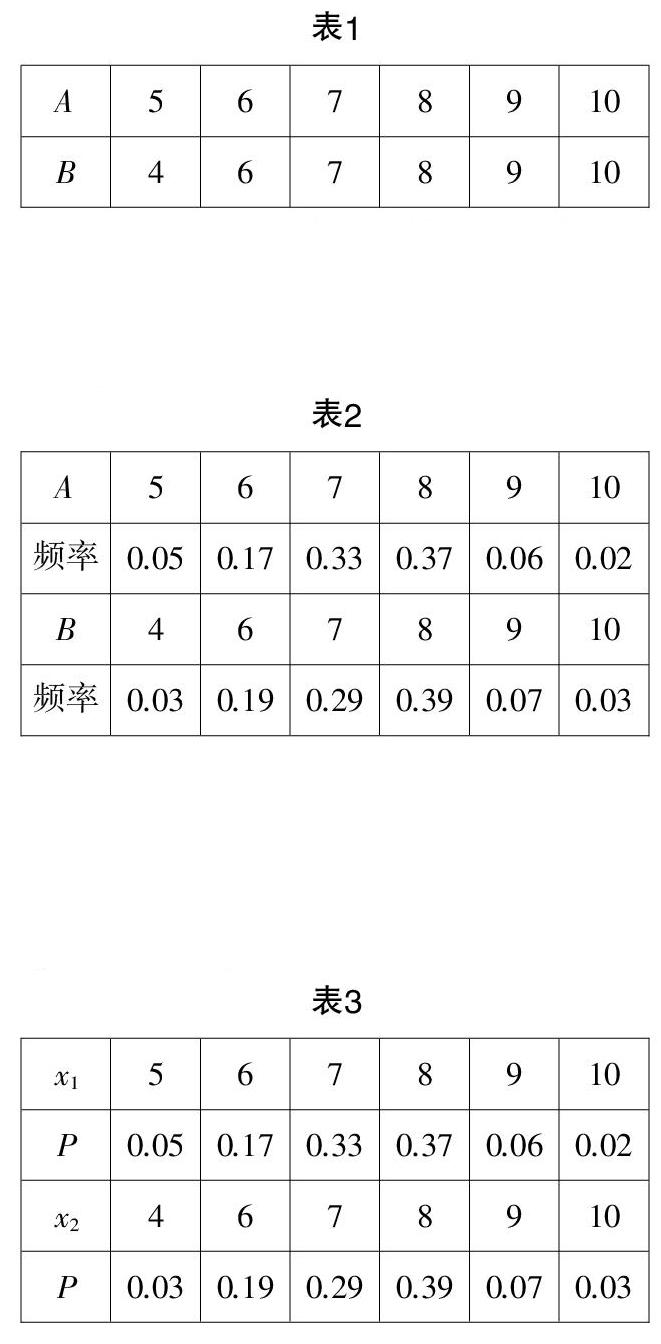
問題1：A，B二人進行了6次射擊比賽，并得出以下成績：

你覺得A與B誰的成績更加穩定呢？

問題2：A，B二人進行了100次射擊比賽，并得出以下成績：

你覺得A與B誰的成績更加穩定呢？

問題3：下表是A，B二人以往參加射擊比賽的成績匯總，其中x1是A的成績，x2是B的成績：

你覺得A與B誰的成績更加穩定呢？

師：請大家合作交流，并解決以上問題. （經過獨立思考和合作討論，學生逐一解決了問題1和問題2，當解決到問題3時卻思維卡殼，找不到解決思路）

師：大家先對比一下問題1和問題2，問題2和問題3，數據有何區別？并試著類比問題1和問題2的均值計算公式去解決你們無從下手的問題3. （學生很快投入到討論和辨析活動中去了）

生1：我發現問題1中每人擊中的環數各只出現了1次，問題2中每人擊中的環數出現的次數不是1且各不相同，而問題3中每人擊中的環數出現的次數沒有規律.

生2：我覺得問題1中每人擊中的環數的出現頻率均是■，而問題2與問題3中，盡管都不相同，但前者表現在“頻率”上，后者則是“概率”.

師：大家的觀察都非常仔細，都能發現3個表格的區別在于頻率與概率，那頻率可否以概率來替代呢？

生3：在之前的學習中，曾經提及當實驗的次數趨近于無窮時，一個事件發生的頻率趨近于一個穩定值，該值即為這個事件發生的概率.

師：現在哪位學生可以來歸納一下它的概念呢？

生4：若隨機變量X分布列入下表：

則可以稱E（X）=x■p■+x■p■+…+xnpn為離散型隨機變量的均值.

師：下面請從以上問題的均值計算公式進行比較，說一說隨機變量的均值與算術平均值、樣本均值有何區別，又有何聯系;并試著舉例說明，他們是否可以相同. 下面請各小組展開討論. （學生又一次進行討論）

……

以上3個問題的設計有效地將學生的注意力引入了主要的關注對象，并將一切不利于概括的因素均排除在外，此為引領學生展開自主探究的一種較好的教學策略. 縱觀整個教學過程，不難看出，學生通過探究、討論和交流，對以上3個問題的數據有了更好的甄別，自然關注到頻率和概率的區別，得出二者的意義，跨越了本節課教學的難點. 在整個過程中，教師給學生預留了足夠的探究空間，注重活動的思維性和有效性，幫助學生自然而然地完成探究，使其在頭腦中不斷進行“再創造”，做到真正意義上的“以生為本”[2].

■靈活變形手段，提升探究能力

隨著教育課程改革的深化和素質教育的推進，傳統教學中的照本宣科式教學模式已然遭到了學生的“遺棄”，課堂教學中的價值取向也逐步由“應試”轉型為“能力”. 因此，在傳授知識的同時，教師要有意識地靈活變形手段，自然滲入變式教學，開發學生思維的靈活性，讓學生在自主探究中培養創新意識，使能力的培養得以落實[3].

案例3：三角函數最值問題

問題：已知函數f（x）=-■sin2x+sinxcosx，試求出f（x）在區間x∈0，■上的最小值.

變式1：已知函數f（x）=-■sin2x+cosx，試求出f（x）在區間x∈0，■上的最小值.

變式2：已知函數f（x）=■+■，試求出f（x）在區間x∈0，■上的最小值.

變式3：已知函數f（x）=■+■，試求出f（x）在區間x∈0，■上的最小值.

以上案例中，教師以“三角函數最值問題”中的一道典型問題為指引，很好地落實了學生的數學基礎，并通過螺旋上升的變式練習，讓學生在主動探究的過程中感受方法和知識. 教師在此要做的更多的是多角度、多層次去設計變式，讓學生去思考、去觀察、去發現、去聯想、去探索，從而得出解決問題的策略，在活動中親身領悟，優化解題方法，從而使探究精神和創新思維的培養落到實處.

總之，學習數學應該是一個積極主動的、生動活潑的、富有個性的過程，這里不僅需要學生從“要我學”轉變為“我要學”，而且還需更進一步從“我要學”轉型為“我會學”. 我們每位數學教師若能深入思考如何去適應新課標的要求，去培養學生自主探究的能力，引導學生用自己的“所有”去探究“所無”，通過自主探究學思考、學創新、學創造，使學生學會思考、學會探究、學會成長、學會發展，我們的數學課堂才是真正精彩的課堂.

參考文獻：

[1]? 謝月華. 讓學生“探索”數學天地的“奧秘”——新課標下初中數學教學中探究性教學策略運用芻議[J]. 新課程（中），2012（09）.

[2]? 張浩. 進步融于探究之中——芻議數學探究能力培養策略[J]. 理科考試研究（高中版），2013，20（07）.

[3]? 任長松. 探究式學習：學生知識的自主建構[M]. 北京：教育科學出版社，2005.