談審辨式復習課新樣態的構建與實施

蔣巧君

審辨思維是指思維活動中善于嚴格估計思維材料和精細檢查思維過程的智力品質，體現著思維過程中獨立分析和批判的程度，應作為問題解決和創造性思維的一個組成部分。我們基于審辨思維“質疑批判、分析論證、綜合生成、反思評價”這四要素，構建審辨式復習課新樣態。

復習課不僅是認知與技能方面的復習與操練，更重要的是問題解決策略方面的復習并會活學活用。為了幫助學生形成解決問題的一些基本策略，北師大版教材在每冊都安排了“數學好玩”，將重點放在學習解決問題的策略上。六下最后一課是“解決問題的策略”，目標是梳理在小學階段常用到的問題解決策略，如畫圖、列表、猜想與嘗試、從特例開始尋找規律等。但教材上安排各種解題策略的數學素材都不相同，策略間的勾連難以體現，而“雞兔同籠”問題能很好地把這些策略串聯起來。以下談談如何開展審辨式復習，如何引領學生在解題方法策略的復習中溫故知新。

一、引發追憶，質疑問難

復習課不同于新課，它沒有固定的教材，應該基于學情的需求有針對性地進行復習。復習課中首先要引發學生對復習內容進行自主追憶。追憶既是提取舊知的過程，也是進一步強化記憶的過程，還是互相啟發獲得聯想結果的過程。在學生追憶的過程中，教師應該創設合適的時空讓學生質疑問難，充分暴露復習的需求點，同時培養學生質疑問難的意識、方法、能力與習慣。在信息爆炸的社會，質疑批判為我們辨別信息來源、分析評價信息內容，進而做出正確選擇和決策奠定了基礎，是分析論證、綜合生成、反思評估發生和發展的基礎。與質疑批判相關的具體行為表現有：對既有的觀點或做法持懷疑態度;能從不同角度不斷提出新問題;堅守真理的相對性，不迷信權威;考慮并包容不同意見，特別是與自己相左的意見。

在本課第一環節，教師在課前放手讓學生自主解題“籠子里有若干只雞和兔，從上面數，有35個頭，從下面數，有94條腿，雞和兔各有幾只？”通過解題引發學生追憶小學階段解決“雞兔同籠”的多種方法，并在四人小組里互相交流討論（有畫圖法、列表法、算術法、方程法等）。教師展示學生的各種解題方法，為他們創設質疑問難的機會：“通過課前對‘雞兔同籠的獨立思考和小組交流之后，現在你對哪種解題方法有疑問？”學生提出自己的疑惑，并由其他同學解說。此時，教師要當好“踢球高手”，把學生的“不懂和疑問”導回到學生中去，讓學生之間的多維互動互評得以開展。

學生用什么方法解決“雞兔同籠”問題，往往體現出他當時所處的思維水平或喜歡選用的解題思路。此時，教師可以提問：“你喜歡用哪種方法解決‘雞兔同籠問題，為什么？”這既能充分暴露學生此時的學情，又能在集中討論辨析中進一步理解其他解題方法，更能體現出對每種解題方法的反思評價。因此，教師應該適時展開“方法選優”，讓習慣于用形象思維解決問題的學困生能夠在掌握畫圖法與列表法后，積極主動地去理解比較抽象的算術法和方程法。

二、觀察思考，辨析論證

審辨思維是提出恰當問題并進行合理論證的能力，包括對各種信息的理解、識別、分析、綜合、比較、判斷等方面的能力，其中，分析和論證能力最為重要，是最常見的審辨思維技能。因此，審辨式復習課在呈現學生思維多元化表征之后，教師要讓學生對它們進行歸類比較，在深度辨析中走向深度思考，進行深度學習，由此得出更深層次的結論，真正實現溫故知新。

“雞兔同籠”復習課在展示學生各種解題策略之后，教師要引導學生仔細觀察板書，辨析論證：如果把畫圖法、列表法、算術法、方程法這四種方法分成兩類，該如何分？為什么這樣分，說說理由。學生可能會作如下分類。

（1）畫圖法、列表法、算術法分為一類，方程法分為一類。理由是：方程法中有未知數“x”，用字母表示數是算術與代數最顯著的區別。

（2）畫圖法、列表法分為一類，算術法、方程法分為一類。理由是：畫圖法、列表法的特點是具體形象，不用式子表示;算術法、方程法的特點是概括抽象，都用式子表示。

（3）畫圖法和算術法分為一類，列表法和方程法分為一類。理由是：畫圖法和算術法假設全部是雞或者兔，算術法就是把畫圖的過程變為算式，畫圖的每一步都對應一個算式。列表法和方程法也有聯系，列表法和方程法兩邊都是未知數。如果雞是1，兔就是（35-1），如果雞是2，兔就是（35-2）……如果雞是x，兔就是（35-x）。每只雞兩條腿，所以要乘2，兔子要乘4，雞腿加兔腿等于94條腿。所以列表法和方程法也是對應的。

該環節通過學生從多角度對方法進行觀察分類、辨析概括，透過不同方法的表象找到不同策略之間的異同。學生在充滿激情的思辨中走向深度學習，呈現了思維的深刻性和獨創性，提高自身審辨思維技能。

三、綜合生成，溫故知新

審辨式復習課既要體現出學生思維深刻性和獨創性的培養，又要充分體現學生思維系統性與宏觀性的培養。“綜合生成”是一種高層次思維能力，它建立在分析和論證的基礎上，最終形成的可能是觀點、策略。在信息紛繁復雜的當今社會，綜合生成將不同信息片段整合成一個新的統一體，有助于我們得到更多解決方案，進而做出正確決策。

“雞兔同籠”復習課在學生對方法進行多維分類辨析之后，教師追問：“這些方法有沒有相通的地方？”學生仔細思考前文第（3）種分類的理由：畫圖法和算術法假設全部是雞或者兔;列表法和方程法兩邊都是未知數，實際上也是假設。學生最終發現畫圖法、算術法、方程法、列表法都在運用假設的思想方法解決“雞兔同籠”問題，只是表現手段多元化而已。

此時，教師再追問：“哪些同學喜歡的解題方法有變化啦？”有些學困生會由原先喜歡列表法改選為喜歡用方程法解決“雞兔同籠”問題。教師及時引導學生反思評價，讓學生感悟到：解決數學問題的方法殊途同歸，沒有最好，只有更好;解題思路越簡潔方便，其思維品質越好。

四、活用策略，提升學力

審辨式復習課的目標不僅是為了讓學生能舉一反三、觸類旁通，更重要的是培養學生能創造性地活學活用解題策略解決新問題。如果在復習課尾只是追求對前面同類題型的“熟能生巧”，長此以往會導致學生解題思路的僵化，結果往往會“熟能生笨”。

“雞兔同籠”復習課的最后環節是解決綜合復習題，與前面題目不一樣，此時需要學生活學活用解題策略。學生即使不能獨立解決該問題，也能在討論交流環節獲得面對新問題要活用策略的意識。

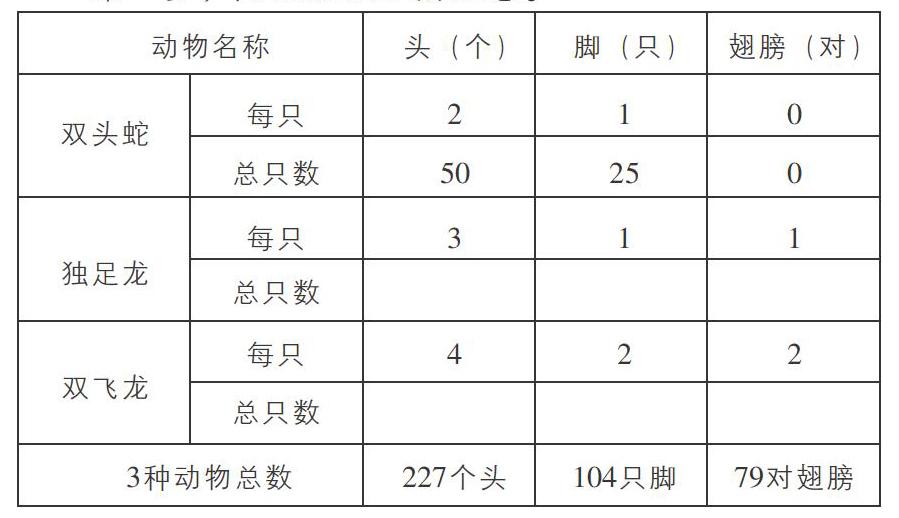
習題：神秘的太空有一個“克洛王國”，這里的動物都非常奇特，有雙頭一腳沒有翅膀的雙頭蛇，有三頭一腳一對翅膀的獨足龍，還有四頭兩腳兩對翅膀的雙飛龍。一天，雙頭蛇家族、獨足龍家族和雙飛龍家族在林間聚會，蘑菇怪數了數發現這些雙頭蛇、獨足龍、雙飛龍一共有227個頭、104只腳、79對翅膀。請你幫蘑菇怪算一算到會的雙飛龍有多少只？

第一步，用圖表法理解題意。

第二步：用假設法求出雙頭蛇的只數。引導學生觀察上表，可知獨足龍一腳一對翅，雙飛龍兩腳兩對翅，假設雙頭蛇也有1對翅膀，那么應該有104對翅膀，而實際上只有79對翅膀，說明“104-79”的差是雙頭蛇的只數，因為雙頭蛇沒有翅膀。

第三步：用算術法求出雙頭蛇的只數。104-79=25（只），雙頭蛇的頭25×2=50（個），“雙頭蛇”的腳有25只;獨足龍和雙飛龍的頭共有“227-50=177（個）”，獨足龍和雙飛龍的腳共有“104-25=79（只）”。

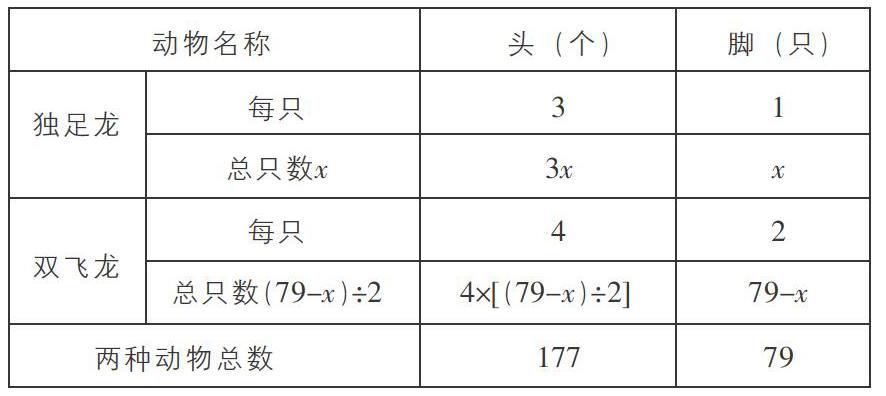
第四步：用圖表法和方程法厘清獨足龍和雙飛龍的數量關系。

根據表中的已知條件，用方程法解決。設獨足龍有x只，那么雙飛龍有（79-x）÷2只。根據題意列出方程：3x+4×[（79-x）÷2]=177，求出方程的解是19，即獨足龍有19只。

第五步：用算術法求出雙飛龍的只數（79-19）÷2=30（只）。

教師也可以根據學情，給學有余力的學生介紹一下“三元一次”方程法，拓展學優生的解題思路。

（作者單位：浙江省義烏復旦實驗學校）