“再發現”是突破教學難點的有效策略①
——《數學歸納法》的課堂實錄與思考

2019-12-26 07:15:26陶兆龍

數學通報 2019年11期

陶兆龍

(江蘇省南京市金陵中學 210005)

突破教學難點一直是教師關注的問題.在長期的教學實踐中，廣大教師總結了很多突破教學難點的方法與措施.這些措施與方法，對于數學知識的學習與理解，確實發揮了良好的作用.但隨著課改的深入，教學理念的更新，我們已經愈來愈清晰地認識到：數學學習不僅僅是為了獲得數學知識與技能，更為重要的是如何提升學生的數學學科核心素養.在核心素養的背景下，突破教學難點，更應關注學生的數學思維過程.因而，“再發現”是突破教學難點的有效策略.本文結合《數學歸納法》的教學實踐，談談如何通過“再發現”來突破教學難點的探索與思考.

1 內容分析

數學歸納法是以數學歸納法原理為根據的演繹推理,它將一個無窮推理過程轉化為一個有限步驟的演繹過程,是證明有關自然數問題的有力工具.

蘇教版2-2將數學歸納法安排在推理與證明這一單元,排在合情推理,數學證明之后,這樣的編排既有利于數學歸納法的教學,也有利于合情推理與數學證明的教學.

推理與證明這一單元的學習可以較為系統地讓學生掌握推理(合情推理與演繹推理)與數學證明的基本方法,對提高學生的邏輯推理能力,培養其數學核心素養有一定的促進作用.這也是本單元教學要達成的重要教學目標.數學歸納法作為本單元的收官之作理應承擔這方面的任務.

數學歸納法教學存在的問題主要有:

(1)數學歸納法的引入過程簡單化,只是強化數學歸納法的解題應用,導致不少學生不能理解數學歸納法原理,尤其是對遞推步不知何意,解題時只會生搬硬套兩個步驟.

較為常見的是通過多米諾骨牌的演示直接引入數學歸納法, 實際上即使經過討論學生也很難將多米諾骨牌與數學歸納法建立起聯系,難以促進學生的理解.

(2)缺乏整體考慮,在進行數學歸納法教學時不關注合情推理.歐拉說過,類比是偉大的引路人，類比和歸納是數學發現的重要工具.在學習了合情推理,數學證明后,如果不聯系這些內容學習數學歸納法,學生不僅難以形成合理的知識結構，也錯過了運用類比與歸納進行“再發現”學習的最好時機.

(3)問題(含例題)的選擇不能體現數學歸納法的優勢,有很多問題不用數學歸納法解決更簡單,強行應用數學歸納法反而使學生感受不到學習新知識的必要性,對數學歸納法的學習產生抵觸情緒,思維活動無法展開.

由以上的分析可以看到,不論從單元教學,還是數學歸納法本身教學出發,數學歸納法的教學都應突出類比與歸納在數學“再發現”過程中的作用，強化邏輯推理這一核心數學素養的培養.

本節課的教學目標：了解數學歸納法原理，能用數學歸納法證明一些簡單的命題，體會演繹推理將無窮歸納過程轉化為一個有限步驟演繹過程的魅力,感受邏輯推理在數學發現和證明中的強大作用.

教學難點是“由n=k推證n=k+1”的遞推過程.

2 課堂實錄

2.1問題情境

師:提出問題: 求和 13+23+33+…+n3=?(記為P(n)=?)

引導學生采用歸納推理形成猜想,并注意利用P(2)算P(3),利用P(3)算P(4).

[教學意圖:由P(2)算P(3)或者P(3)算P(4)一是簡化計算,更重要的是為后面的遞推作鋪墊]

生:猜想:

師:上述猜想是否正確呢?怎樣判斷?

生:利用猜想再算幾個看看!

……

師:回顧一下前面的討論,實際上是這樣的一個思路:

P(4)?P(5)?P(6)?P(7)?……

這樣依次由前一個推出后一個,推算的再多也只是有限個,也不能保證猜想對所有正整數都成立.

既然由特殊不能推一般,那么應該怎樣推證?

生:……一般化,由一般推一般!

師:你這里是利用

來推證

13+23+33+…+k3+(k+1)3

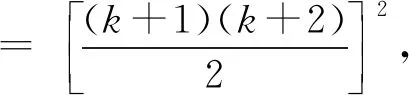
[教學意圖:幫助學生理清思路,有不少學生還沒弄清是怎么回事]

師:但是P(k)是不是正確,還沒有證明啊?

生:假設它成立.

師:怎么敢假設它成立呢?

[教學意圖:這里是一個疑點,關系到學生對數學歸納法的理解,要作停頓,逼學生交待清楚!]

生:P(k)是否為真可以先不看,只要看命題:P(k)?P(k+1)是否為真即可.

師:哦,上面的證明實際上是得到這樣一個結論:假如P(k)為真,則P(k+1)也為真.那這樣能保證上面的猜想成立嗎?

生:可以,因為k可以取任意正整數,所以對任一個正整數n,有

P(1)?P(2)?P(3)?P(7)?P(8)…

?P(n)

師:這一招真好,一招制勝!

只要這一招就行了嗎?

[教學意圖:闡明數學歸納法的兩個步驟的必要性]

生(討論):沒有P(1)成立不行,無法啟動.

師: 兩個步驟缺一不可!

觀看多米諾骨牌視頻(蘋果手機廣告片),讓學生討論怎樣才能保證骨牌全部倒下?

最終得出結論:

(1)前一張倒下要能推倒后一張,(2)推倒第一張.

再與與前面的問題相比較,弄清其中蘊含的遞推思想: “(1)前一張倒下要能推倒后一張”相當于“命題:P(k)?P(k+1)是否為真”,而“(2)推倒第一張”相當于P(1)成立.

[教學意圖:先解決前面的問題,再演示多米諾骨牌視頻,為前面較為抽象的方法提供一個直觀的背景,通過對比,有利于學生進一步理解前面的方法]

師: 我們前面解決問題的方法就是以下的數學歸納法公理.

2.2數學理論

對于某些與正整數有關的數學命題，我們有數學歸納法公理：

(1)當n取第一個值n0(例如n0=1，2等)時結論正確；

(2)假設當n=k(k∈N*，且k≥n0)時結論正確，證明當n=k+1時結論也正確.

那么，命題對于從n0開始的所有正整數n都成立.

師: 有了上述公理,要解決與正整數有關的問題,可以采用數學歸納法,只要看其是否滿足(1)(2)兩步即可.

由上面的討論可知,第(2)步實際上就是要證明一個結論:“P(k)?P(k+1)”,所以要先假設P(k)成立,再由此推證P(k+1)成立.

2.3數學應用

例1：用數學歸納法證明：

給出完整的證明過程.

[教學意圖:讓學生熟悉數學歸納法證明的流程,了解有關的書寫規范]

最后指出:在用歸納推理得到猜想后,由數學歸納法進行了嚴格的證明,得到了我們需要的結論.歸納讓我們得到猜想,用數學歸納法給出嚴格的證明,先猜后證,相得益彰.

例2：求和：12+22+32+…+n2=?

歸納推理受阻后,引導學生類比

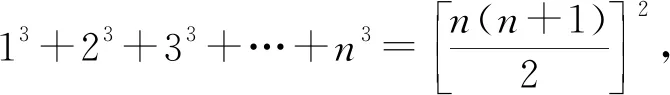
得出猜想: 結果應該是關于n的三次式,但系數不好猜!

師:猜的合理吧? 即

12+22+32+…+n2=an3+bn2+cn+d.

現在的問題是:a,b,c,d能否想辦法求出來?

生:特殊化,n取4個特殊值1,2,3,4,可以求出a,b,c,d.

師:現在我們得到

這個結果還需要證明嗎?

生:要！結果是猜出來的,要用數學歸納法證明.

師: (在讓學生寫出證明后)回顧一下,是怎么猜出來的?

生:類比和特殊化.

師:和例1采用歸納推理作出猜想不同,我們用類比的方法猜出右端應為關于n的三次式,再用特殊化的方法求出系數,最后用數學歸納法進行了論證.

合情推理可以幫助我們發現結論,得到猜想,數學歸納法使我們多了一種嚴格證明有關猜想成立的方法.有數學歸納法保駕護航,我們就可以大膽地進行有關猜想!

2.4課堂練習

設n為正整數,試比較2n與n2的大小.

最后指出

(1)n的初值n0不一定是1.

(2)僅由P(k)?P(k+1) 不能保證結論正確.

[教學意圖：本題的結論較復雜,正確結論是

21>12; 22=22; 23<32; 24=42,當n≥5時,2n>n2.

但當k≥3時,

若2k>k2,則2k+1>2k2,

2k2-(k+1)2=k2-2k-1=k(k-2)-1,

上式大于0，所以2k+1>2k2>(k+1)2，

即可由P(k)?P(k+1),

但23<32, 24=42與2n>n2矛盾.這表明遞推步不能保證命題成立.因此,本題可以進一步訓練學生歸納猜想能力,加深對數學歸納法兩個步驟缺一不可的認識]

2.5課堂小結

(1)討論:用數學歸納法證明有關正整數問題的兩個步驟及表達規范，強調遞推步實際上是證明一個命題“P(k)?P(k+1)”成立.

(2)合情推理讓我們體驗到數學發現的樂趣,而數學歸納法又使我們感受到了演繹推理

的力量,這種感覺真好!

3 教學思考

普通高中數學課程目標要求通過高中數學課程的學習，學生能夠獲得進一步學習以及未來發展所必需的數學“四基”(包括基本思想、基本活動經驗)，提高“四能”.在學習和應用數學的過程中發展數學學科核心素養.普通高中數學課程標準還提倡教師要善于根據不同的內容和學習任務采用不同的教學方式，優化教學，抓住關鍵的教學和學習環節，增強實效.

在日常教學中，教學難點幾乎是師生每節課都要面臨的問題，所以教學難點的破解策略直接關系到高中數學教育目標的落實.作為課堂教學關鍵環節教學難點的教學不能僅僅滿足于使學生理解有關內容，還應承擔發展學生數學核心素養的任務.

3.1“再發現”是突破教學難點的有效策略

怎樣在突破教學難點的同時，學生的數學核心素養也得到一定的培育？

普通高中數學課程標準大力提倡教師注意引導學生獨立思考、自主探索、合作交流.

荷蘭著名數學教育家弗賴登塔爾認為，通過再創造(再發現)獲得的知識與能力要比被動方式獲得者，理解的更好，也更容易保持.

“再發現”是我們突破教學難點的必然選擇.

“再發現”不是讓學生完全經歷數學家發現或發明數學的過程，而是基于學生的數學現實(原有的認知結構)，讓學生在教師的引導下運用數學思維方法與數學思想方法，經歷操作、實驗、猜想、想象、類比、歸納、交流、概括、反思等有意義的數學活動，實現數學化.

引導學生運用“再發現”學習數學知識，實際上就是讓學生主動地參與到新知識的產生過程中去,由于數學思維方法與數學思想方法的運用可以極大地提高發現和提出問題、分析和解決問題的效率，因此，“再發現”可以有效地突破教學難點，與此同時，數學思維方法與數學思想方法學習或應用促進了數學核心素養的發展.

在本節課的教學中，針對學生學習數學歸納法存在的困難，采用了“再發現”的教學策略，在教師的引導下,學生們通過自主探索、合作交流實際上“再發現”了數學歸納法,取得了較好的教學效果.

3.2“再發現”需要精心設計與有效引導

從上述教學過程看，“再發現”突破教學難點教學策略的有效實施，離不開教師的精心設計與有效引導，以下兩個方面值得關注.

3.2.1 “再發現”需要好問題的驅動

數學歸納法引入或應用的教學中,如果選用一些簡單的不用數學歸納法也能解決的問題(例題),那么學生就會對數學歸納法產生疑問：學習這一方法干嗎?學生的思維會完全處于抑制狀態.本節課中選擇的三個問題,充分體現出數學歸納法的應用價值,還解決了困擾他們很久的問題:會猜想而不會證明.這樣的選擇,激發了學生學習數學歸納法的興趣,激活了學生的思維.引入部分的問題對學生來說有一定的挑戰性，通過合作交流得到猜想使他們得到了成功的體驗，問題的解決最終帶來了新知識的“再發現”.課堂上學生情緒飽滿,討論熱烈,取得了很好的教學效果.

“再發現”需要好問題的驅動.突破教學難點時，教師首先要對新知識的形成、發展過程作出邏輯模擬，在此基礎上設計好適合學生數學現實的問題，然后引導學生運用數學思維方法和數學思想方法分析問題、解決問題，從而發現新知識.

3.2 .2 “再發現”需要聚焦思維過程

教學難點的確定并非輕而易舉的事.要突破突破教學難點，首先要準確地確定教學難點.

這就需要教師聚焦學生的思維過程，進行換位思考.精準地定位后才能有的放矢地去破解.

本節課的教學難點是“遞推步”，學生對此感到難以理解：明明是要證明P(n)，卻竟然假設P(k)成立！不是循環論證了嗎？

所以在教學過程中,抓住機會，直面這一難點,反問提出設P(k)成立的同學,怎么可以這樣做(假設P(k)成立!)？這個問題實際上是替學生問的,提出了他們的困惑!而問題解法的本質是要推證出一個真命題“P(k)?P(k+1)”,即:如果P(k)成立,那么P(k+1)也成立.

這樣的處理使學生厘清了“遞推步”的真實含義,對學生理解數學歸納法至關重要.

由學生提出“由一般到一般”的想法,老師再去質疑,是教學設計時最希望出現的場景,實際上就是希望學生能夠“再發現”數學歸納法.為了達到這一目的,新課引入部分的問題設計及解決問題過程中的鋪墊(P(2)?P(3)…)都起到了推波助瀾的作用.

即使沒有學生提出這樣的思路,老師還可以進一步引導 “既然由特殊不能推一般,那么由什么可以推一般?” ,“P(k)?P(k+1)”是什么意思?怎么可以假設P(k)成立?等等。

充分的數學活動可以將學生的困惑，想法暴露無遺，再加上教師疑學生所疑,思學生所思,師生,生生之間就會產生思維碰撞,再發現就有可能產生，教學難點的突破就會水到渠成.

3.3“再發現”是發展數學核心素養的需要

從課堂教學的效果來看,在“再發現”的過程中合情推理與演繹推理的聯袂使用起到了多米諾骨牌根本無法替代的作用!這種經歷和感受對發展學生的邏輯推理素養意義重大，發展學生的數學核心素養離不開“再發現”，“再發現”不僅是突破教學難點的有效策略，也是發展學生數學學核心素養的需要.

課堂上有學生提出一般化的思路：“由一般推一般，即P(k)?P(k+1)”并非偶然.滴水穿石非一日之功,這是我們長期堅持不懈地運用“再發現”的策略進行有關訓練的結果.

邏輯推理能力持續不斷地訓練提升了學生“再發現”的能力，能促使“再發現”的發生，而“再發現”的產生又進一步激發了學生學習合情推理的熱情，兩者相輔相成，相得益彰.