閔科夫斯基平面M2和閔科夫斯基變換

趙旭安

(北京師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，教育部數(shù)學(xué)和復(fù)雜系統(tǒng)重點(diǎn)實(shí)驗(yàn)室 100875 )

平面歐氏幾何是中學(xué)數(shù)學(xué)教學(xué)的重要內(nèi)容.對(duì)其中的經(jīng)典結(jié)果，人們非常熟悉.而對(duì)和歐氏幾何完全平行的另一種幾何，閔科夫斯基幾何，很多人都不了解.閔科夫斯基幾何和歐氏幾何有諸多相似之處，但也有一些本質(zhì)的差異.利用閔科夫斯基變換可以很容易地解釋狹義相對(duì)論中關(guān)于運(yùn)動(dòng)的參照系中所謂的尺縮和鐘慢效應(yīng).本文不討論閔科夫斯基幾何的物理背景，只介紹相關(guān)的幾何內(nèi)容.下面為了敘述方便，我們把閔科夫斯基幾何簡稱為閔氏幾何.

平面歐氏幾何是空間的幾何，而平面閔氏幾何是時(shí)空的幾何.如果選取適當(dāng)?shù)淖鴺?biāo)系，兩個(gè)歐氏坐標(biāo)都是空間坐標(biāo)，而閔氏坐標(biāo)同時(shí)包含時(shí)間坐標(biāo)和空間坐標(biāo).愛因斯坦革新了牛頓的存在獨(dú)立的時(shí)間和空間的錯(cuò)誤認(rèn)識(shí)，將對(duì)引力的研究歸結(jié)為對(duì)時(shí)空幾何的研究.本文也秉承這一思想，在討論中將閔氏幾何的坐標(biāo)用(x,y)而不是(x,t)表示，這樣也可以更好地與歐氏幾何進(jìn)行比較.根據(jù)Klein關(guān)于幾何學(xué)的觀點(diǎn)，研究一種幾何，首先要看這種幾何允許什么樣的變換.因此下文會(huì)仔細(xì)介紹平面閔科夫斯基變換的概念.

1 閔科夫斯基平面M2

首先我們引進(jìn)閔氏平面M2的概念.在平面上選取原點(diǎn)O和坐標(biāo)軸x,y軸，對(duì)于向量(x,y)，定義閔科夫斯基度量d2(x,y)=x2-y2.如果這里將減號(hào)改為加號(hào)，我們的就得到歐氏度量.平面帶上閔科夫斯基度量稱為閔科夫斯基平面，簡稱閔氏平面.對(duì)于歐氏情形，d2(x,y)≥0成立，可以開方得到距離d(x,y).對(duì)于閔氏情形，d2(x,y)可以大于、小于或等于零，一般不能開方.因此可以給出以下定義.

定義1若d2(a)>0，=0或<0，則稱向量a=(x,y)為類時(shí)、類光或類空向量.

類光向量a=(x,y)滿足x2-y2=0，它們給出平面上過原點(diǎn)的兩條直線，稱為原點(diǎn)處的光錐.光錐(兩條相交直線)將平面分成四部分，左右兩部分中點(diǎn)的坐標(biāo)滿足x2-y2=k2>0，上下兩部分中點(diǎn)的坐標(biāo)滿足x2-y2=-k2<0.

在歐氏幾何中，曲線x2+y2=1稱為單位圓，它是非常重要的幾何對(duì)象.而在閔氏幾何中，沒有圓的概念.其原因在于圓在歐氏變換(平移、旋轉(zhuǎn)和反射)下仍然變成圓.而這一性質(zhì)在閔氏變換下不再成立.單位圓x2+y2=1的參數(shù)方程大家都很熟悉，它可以由x=cos(t),y=sin (t)給出，這里t是歐氏的角度參數(shù).在閔氏幾何下，最重要的曲線是將單位圓的方程中加號(hào)變成減號(hào)得到的單位雙曲線x2-y2=1.

在歐氏情形下，我們有

引理1單位圓周x2+y2=1的參數(shù)方程為x=cos(t),y=sin (t)，這里t滿足0≤t<2π.

證明設(shè)x2+y2=1，則有(x+iy)(x-iy)=1.這說明(x+iy)和(x-iy)都是單位復(fù)數(shù).于是存在實(shí)數(shù)t使得x+iy=eit，且x-iy=e-it.根據(jù)歐拉定理eit=cos(t)+isin (t)可知引理成立.

順便地我們得到了

和歐氏情形不同的是雙曲線x2-y2=1包含兩個(gè)連通分支，如果我們只選取x>0的分支，則相應(yīng)的參數(shù)方程為

下面我們通過求參數(shù)方程的過程，也可以得到閔氏幾何類似于角度的參數(shù).

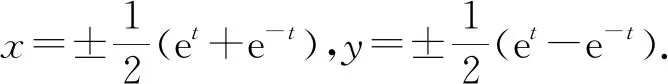
如果和歐氏情形進(jìn)行比較，不難看出這里的參數(shù)t也具有某種類似角度的屬性，差別是這里參數(shù)t的取值范圍是整個(gè)實(shí)數(shù)軸.

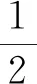
上面結(jié)果進(jìn)一步說明閔氏和歐氏情形之間存在緊密的聯(lián)系.對(duì)應(yīng)于與三角函數(shù)的等式cos2(t)+sin2(t)=1.我們有雙曲三角函數(shù)對(duì)應(yīng)的結(jié)果cosh2(t)-sinh2(t)=1.

為了書寫方便，下面我們把cosh和sinh簡寫為ch和sh.

2 閔科夫斯基變換

為了定義平面閔氏變換，我們先討論歐氏情形是如何定義的.平面歐氏變換群Euc(2)包含平移、旋轉(zhuǎn)和反射三種基本的變換.

下面我們定義平面閔氏變換群Min(2).它包含平面上的平移變換群及平面上保持原點(diǎn)不動(dòng)的子群O(1,1).這里O(1,1)稱為(1,1)型的正交群.

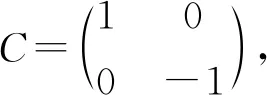
下面我們來求T的具體形式.將TtCT=C寫成分量形式得到

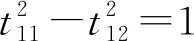
這里有四類解的原因是關(guān)于時(shí)間和空間都可以做反射.

定義5參數(shù)為t的閔氏旋轉(zhuǎn)由表達(dá)式

給出.對(duì)應(yīng)于上面其它三種矩陣的變換分別是閔科夫斯基旋轉(zhuǎn)和關(guān)于x軸、y軸的反射的復(fù)合變換和關(guān)于原點(diǎn)的中心對(duì)稱的復(fù)合變換.

根據(jù)定義不難看出閔氏變換把平面上的雙曲線x2-y2=k2，x2-y2=-k2<0和光錐保持不變.閔氏旋轉(zhuǎn)可以把雙曲線x2-y2=1某一分支的一點(diǎn)旋轉(zhuǎn)至此分支上的任意其它點(diǎn).平面上關(guān)于x軸的反射將坐標(biāo)y變號(hào)，并且保持坐標(biāo)x不變；關(guān)于y軸的反射將坐標(biāo)x變號(hào)，并且保持坐標(biāo)y不變.利用這兩種反射及其復(fù)合變換可以把平面上一點(diǎn)變換到第一象限(包括邊界)或者把光錐分割出的左右(或者上下)兩個(gè)區(qū)域相互交換.容易驗(yàn)證參數(shù)為s的閔氏變換將雙曲線x2-y2上參數(shù)為t的點(diǎn)變?yōu)閰?shù)為s+t的點(diǎn).這類似于歐氏平面上的參數(shù)為θ的旋轉(zhuǎn)將單位圓上參數(shù)為φ的點(diǎn)映為參數(shù)為θ+φ的點(diǎn).

參數(shù)s的閔氏旋轉(zhuǎn)和參數(shù)t的閔氏旋轉(zhuǎn)的復(fù)合是參數(shù)s+t的閔氏旋轉(zhuǎn).這在代數(shù)上等價(jià)于公式ch(s+t)=ch(s)ch(t)+sh(s)sh(t)和sh(s+t)=ch(s)sh(t)+sh(s)ch(t).讀者可以利用雙曲函數(shù)的定義與指數(shù)函數(shù)的性質(zhì)直接證明.

一個(gè)一般的閔氏變換是O(1,1)中變換和一個(gè)平移變換的復(fù)合變換.它具有形式

(x,y)=(x′,y′)T+(x0,y0).

對(duì)于歐氏情形有以下簡單的結(jié)論.

命題1E2中的任一向量a=(x,y)可以通過以原點(diǎn)為中心的歐氏旋轉(zhuǎn)變換變成標(biāo)準(zhǔn)形式(k,0),k>0或者(0,0).

對(duì)于閔氏幾何，事情會(huì)更復(fù)雜一些.

命題2M2中的任一向量a=(x,y)可以通過以原點(diǎn)為中心的閔氏旋轉(zhuǎn)和關(guān)于x和y軸的反射變換變成四類標(biāo)準(zhǔn)形式(k,0),(0,k),k>0,(1,1),(0,0)之一.

證明任取一點(diǎn)，設(shè)其坐標(biāo)為(x,y).若a=(0,0)，則它變?yōu)?0,0).若它在光錐上，且不是原點(diǎn)，則x2-y2=0，利用反射可以將它變?yōu)?x,x),x>0.再通過閔氏旋轉(zhuǎn)可以變?yōu)?/p>

=(x,x)et

若x>0，通過選取適當(dāng)?shù)膖可以使得(x,x)et=(1,1).

類似的若x2-y2=k2>0，則能夠?qū)?x,y)變?yōu)?k,0)；若x2-y2=k2<0，則(x,y)可以變?yōu)?0,k).讀者可以自己去驗(yàn)證.

3 閔科夫斯基空間的直線和二次曲線的分類.

歐氏平面上的任意直線可以通過歐氏變換變成x軸.閔氏平面上的直線可以通過閔氏變換變成x軸、y軸或者直線y=x.出現(xiàn)這三種情形是因?yàn)橹本€的方向向量有類時(shí)、類空和類光三種情形.

我們也可以討論閔氏空間中的二次曲線的分類，因?yàn)榉诸惐容^復(fù)雜，所以不再贅述.讀者可參考文獻(xiàn)[1]中歐氏情形的討論，自己嘗試去給出相應(yīng)結(jié)果.