老師，我為什么算得這么慢
——導數篇

江蘇省蘇州中學 王思儉

考完試后有幾位同學議論：

解答題第19題運算量超大，有的結果超繁瑣，單調區間含有根式；

填空題最后兩題運算量太大了，如同解答題，題目條件不知道怎么用；

暑假期間我刷了很多高考導數壓軸題，各地38套模擬題，但有的題還是不會做；

看來只刷題并不能真正提高運算速度，必須要加強解題回顧；

我在運算方面的經驗是：概念定理要清晰、方法策略要合理、運算步驟要簡潔、解題過程要嚴謹、答案結論要規范、解題回顧要常看，簡稱清晰、合理、簡潔、嚴謹、規范、常看；

……

為此邀請五位同學就“導數及應用問題的運算”進行交流，旨在提高他們的運算質量和速度，提升數學核心素養.

生甲：關于函數f（x）=（x2-2x）ex的判斷正確的是（ ）

（A）f（x）既有最大值，也有最小值 （B）f（x）只有最大值，沒有最小值

（C）f（x）只有最小值，沒有最大值 （D）f（x）既無最大值，也無最小值

因為f′（x）=（x2-2）ex，令f′（x）=0，得列表討論知，當時，f（x）有極大值當時，f（x）有極小值.故選A.

生乙：根據其圖象類似于三次函數圖象，應該選D.

教師：你們有沒有研究函數f（x）的圖象，函數f（x）有幾個零點？

生丙：f（x）只有兩個零點，當x＜0時，f（x）＞0，且x→-∞時，f（x）→0；當0＜x＜2時，f（x）＜0，當x＞2時，f（x）＞0.而且，當時，f（x）單調遞減，當時，f（x）單調遞增，因此，當時，f（x）有極小值，也是最小值.所以選C.

教師：很好！分析正確.其圖象大致為圖1.

生乙：函數（其中a為常數）在開區間（2，3）內存在極小值，則a的取值范圍為_______.

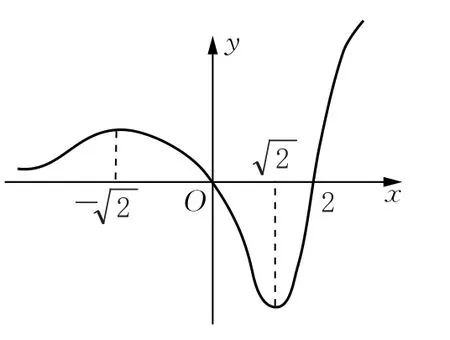
圖1

生丙：雖然答案正確，但過程不嚴謹，應該分類討論，當a≤2時，解出當2＜a＜4或a≥4時，經過討論不等式無解.

生丁：分離變量法求解，因為a（x-1）=x2-2x，x∈（2，3），因此，令x-1=t∈（1，2），轉化為求函數值域，利用單調遞增，值域為）.故a的取值范圍為

教師：很好！生丁的運算簡潔明了，不同的運算策略，解題鏈長短大不相同，因此，要想使運算速度快，結果又正確，同學們必須要學會從不同角度思考問題，積累經驗.

若題目改為：

選擇哪種方法求解呢？

生戊：利用二次函數圖象分析法求解，接上述過程，函數g（x）=x2-（a+2）x+a在（-1，2）內有兩個零點的充要條件為Δ＞0且g（-1）＞0且g（2）＞0且解之得所以a的取值范圍為

生丁：利用分離變量法與幾何直觀法，令x-1=t∈（-2，0）∪（0，1），作出函數圖象，當時，直線y=a與函數圖象有兩個不同交點.

教師：兩種解法都是基本方法，但后一種解法的運算量較小，速度較快.

生甲：若函數f（x）=x3+ax2+cx+2在（0，+∞）內有且只有一個零點，且f（x）-2是奇函數，則f（x）在[-2，3]上的最大值與最小值的和為_________.

根據奇函數求出a=0后，求出f（x）=x3+cx+2的導數f′（x）=3x2+c.但怎樣使用條件“在（0，+∞）內有且只有一個零點”？因此就沒有解下去.

教師：該函數是奇函數向上平移兩個單位而得到的，你分析三次函數圖象與零點個數關系了嗎？

生甲：我討論當c≥0時，在（0，+∞）上無零點，不合適；當c＜0時，求出f′（x）=0的解，經過列表討論知，極大值點極小值點x2=在（0，+∞）內，還是沒有辦法確定c的值.所以最終的答案是含有c的式子.

教師：函數零點和極值點的概念一樣嗎？

生丙：因為f（x）在（0，+∞）內有且只有一個零點，因此f（x）有極小值為0，即解之得c=-3.再計算區間端點的值和極值，可得最大值為20，最小值為0，故答案為20.

教師：正確.利用函數的極值再結合函數圖象控制零點的個數，這種數形結合思想是高考中常考的思想方法，你們應該學會靈活運用數學思想方法解題，這樣才會提高解題能力.

若改為：

求f（x）在[t，t+1]上的最大值與最小值之差g（t）的解析式.

如何解決呢？

生戊：求出極大值與極小值，然后就極值點在區間[t，t+1]外和內進行分類討論，當極值點在內部時，作差f（t+1）-f（t）與0比較大小.答案為：當t≤-2或t≥1時，g（t）=3t2+3t-2；當時，g（t）=-t3+3t+2；當時，g（t）=-t3-3t+4；當-1＜t＜0時，g（t）=-3t2-3t+2；當時，g（t）=t3-3t+2；當時，g（t）=t3+3t2.

教師：非常好！

生甲：已知函數f（x）=（ax2-2x）ex（其中a為常數）.

（1）求f（x）的單調區間；

（2）若a≠0，記函數f（x）的極大值為M，極小值為m，求證：為定值.

我只做出（1），第（2）題不會，但結果太繁瑣了，因為f′（x）=（ax2+2（a-1）x-2）ex，令f′（x）=0，得ax2+2（a-1）x-2=0（*）.因為Δ=4（a2+1）＞0，f′（x）＞0，即ax2+2（a-1）x-2＞0，解之得，或f′（x）＜0，即ax2+2（a-1）x-2＜0，解之得

教師：你確定方程（*）是一元二次方程嗎？

生甲：需要分類討論，a≠0與a=0的情況，若a≠0，就是上述情況，若a=0，此時f′（x）=-（x+1）ex，若f′（x）＞0，則x＜-1，若f′（x）＜0，則x＞-1.

生乙：上述結果是a＞0時的情況，當a＜0時，f′（x）時開口向下的二次函數，相應解集與a＞0的情況相反，即f′（x）＞0解為f′（x）＜0的解為或

教師：在a＜0的情況下，你比較的大小了嗎？

生丙：根據二次函數零點與二次不等式的解，f′（x）＞0，解之得，解之得，或

綜上所述，當a=0時，f（x）單調增區間為（-∞，-1），單調減區間為（-1，+∞）；當a＞0時，f（x）單調增區間為）和），單調減區間為；當a＜0時，f（x）單調增區間為單調減區間為）和

教師：正確！利用導數求函數單調區間，實質就是解含有參數a的不等式，需要分類討論，同時要結合二次函數圖象與二次不等式解的關系求解，充分運用幾何直觀想象.

生丁：由（1）知，當a≠0時，方程（*）有兩個不同的解.由（1）的討論知，x1，x2是函數f（x）的兩個極值點，因此Mm=f（x1）f（x2）=將x1+x2和x1x2代入得，，所以為定值.

眾生：我們是先將x1，x2代入求出f（x1），f（x2），再計算其乘積，運算量特別大，而且繁瑣.

教師：正確！本題先判斷極大值點和極小值點，要先化簡再求值，再利用根與系數關系求解.

生乙：已知函數的極值點構成數列為｛xn｝（n∈N*）.

（1）求數列 ｛xn｝（n∈N*）的通項公式，并證明｛xn｝（n∈N*）為等差數列；

（2）求證：數列｛f（xn）｝（n∈N*）是等比數列；

教師：正確！關于極值點問題和證明等比數列，一定要嚴格按照定義求解，即回到定義去，這是解決問題最基本的方法.

生丙：不等式等價轉化為.構造函數g（x）=于是令g′（x）=0，得x=1，經過列表討論知，x=1時，g（x）有極大值，也就是最大，所以

生戊：不對，x=1時n無解，因此要比較與對應的函數值大小因為因此，）即，g（x）max=所以，故a的取值范圍為

教師：正確！因為x=1實質就是數列｛xn｝中的某一項為1，即無正整數解.

關于導數及應用的運算問題：

首先，要弄清楚題目中所涉及的概念及運算法則，如導數的四則運算法則和常用函數的求導公式，再如“在某一點處的切線”與“過某點的切線”，再如“零點與極值點”等等；

其次，理清要求的結論與題設條件的關系，抓住關鍵詞，如“函數在某區間是單調函數”，再如“求含有參數的函數的單調區間”“不等式在某區間上恒為正數或圖象在x軸上方”等；

再次，選擇正確合理的運算方法及解題策略，如函數與方程、分類討論、數形結合、等價轉化、構造法等；

最后，解題過程要簡潔明了，嚴謹規范，答案正確.如“極值點”是“數”而不是有序數對，再如取值范圍的區間端點能否取到等，都要仔細檢查核對.

同時還要加強解題回顧，對于同一個問題，要學會從不同角度去思考、分析，想一想還有沒有其他解法，能否推廣，改編原題，如“ex”與“lnx”可以互換嗎，“乘積”可以改為“相除”嗎，等等.只有這樣，才能提升你們的解題能力，才能提高你們的解題速度，才能提升你們的核心素養！

1.已知函數f（x）=cosx+ax在[0，π]上單調遞增，則實數a的取值范圍為_______.

（1）求過原點作曲線f（x）切線的方程；

（2）求函數f（x）在區間[k，k+1]（k為常數）的最大值（用k表示）.

答案：

1.[1，+∞）.2.a的取值范圍為

4.（b-a）min=

5.（1）切線方程為y=2x或y=ex.