優(yōu)化“農(nóng)夫式”課堂教學(xué) 培養(yǎng)學(xué)生創(chuàng)新能力

劉宗安 柯炳春

摘? ?要：結(jié)合初中數(shù)學(xué)“農(nóng)夫式”課堂教學(xué)實(shí)踐，從觀察歸納型、開放型、閱讀理解型、方案設(shè)計(jì)型、探究型等五種解題類型的設(shè)計(jì)，闡述如何優(yōu)化“農(nóng)夫式”課堂教學(xué)， 培養(yǎng)學(xué)生創(chuàng)新能力.

關(guān)鍵詞：“農(nóng)夫式”課堂教學(xué);教學(xué)實(shí)踐;創(chuàng)新能力

引言

創(chuàng)新能力是社會(huì)發(fā)展的需要，是新時(shí)期社會(huì)對(duì)人才的要求.培養(yǎng)學(xué)生的創(chuàng)新精神和實(shí)踐能力是新時(shí)期義務(wù)教育課程改革的重點(diǎn)，也是初中數(shù)學(xué)教育的重點(diǎn)，更是培養(yǎng)人才的需要.初中數(shù)學(xué)“農(nóng)夫式”課堂教學(xué)是一種建立在激發(fā)學(xué)生學(xué)習(xí)興趣的基礎(chǔ)上，讓學(xué)生會(huì)學(xué)、愛學(xué)、樂學(xué)的數(shù)學(xué)課堂教學(xué)模式.本文結(jié)合近幾年來的教學(xué)實(shí)踐，就如何優(yōu)化“農(nóng)夫式”課堂教學(xué)，培養(yǎng)學(xué)生創(chuàng)新能力，談點(diǎn)粗淺的看法.

1? “農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)“觀察歸納型”問題，培養(yǎng)學(xué)生的創(chuàng)新能力

【例題1】觀察下列算式： 21=2，22=4，23=8，24=16，25=32，26=48，27=128，28=256，…，則2+22+23+24+25…+22018的未位數(shù)字是__________________.

【簡(jiǎn)析】通過觀察發(fā)現(xiàn)：2n的未位數(shù)字是四個(gè)一循環(huán)，分別為2，4，8，6.因?yàn)?018÷4=504…2，所以22018的未位數(shù)字與22的未位數(shù)字一樣，都是4，從而得出本題答案.本題考查的是尾數(shù)特征，根據(jù)題意找出數(shù)字循環(huán)的規(guī)律是解答此題的關(guān)鍵.

【答案】6.

【點(diǎn)評(píng)】觀察歸納型問題要求學(xué)生用歸納方法從實(shí)例中發(fā)現(xiàn)其存在的規(guī)律，把潛藏在表面現(xiàn)象中的本質(zhì)挖掘出來，當(dāng)規(guī)律被找出后就達(dá)到了創(chuàng)新的目的，這符合學(xué)生的認(rèn)識(shí)規(guī)律，也為創(chuàng)新能力的培養(yǎng)提供了前提條件.

2? “農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)“開放型”問題，培養(yǎng)學(xué)生的創(chuàng)新能力

【例題2】如圖1，在四邊形ABCD中，∠ACB=∠ACD，要使△ABC ≌△ADC，則應(yīng)添加的條件是? ? ? ? ? ? ?.（添加一個(gè)條件即可） .

【簡(jiǎn)析】本題已知一邊（公共邊）和一角對(duì)應(yīng)相等，要使△ABC ≌△ADC，有三種思路可供選擇：（1）若依據(jù)SAS，則應(yīng)填BC=DC;（2）若依據(jù)ASA，則應(yīng)填∠BAC=∠DAC。（3）若依據(jù)AAS，則應(yīng)填∠B=∠D.本題主要考查學(xué)生對(duì)全等三角形判定定理掌握的熟練程度，此類添加條件題是開放型問題，答案并不唯一，只要符合全等三角形的判定定理即可.

【答案】BC=DC或∠BAC=∠DAC或∠B=∠D.

【點(diǎn)評(píng)】開放性問題常提供一些在問題的條件、結(jié)論、解題策略或應(yīng)用等方面具有一定的開放程度的問題，解題時(shí)要靈活運(yùn)用所學(xué)基礎(chǔ)知識(shí)，多層次多角度地分析、思考問題.開放性問題可以使學(xué)生從不同角度去探索，留給學(xué)生更多的空間去發(fā)揮創(chuàng)造，從而培養(yǎng)學(xué)生的創(chuàng)新能力.這類問題有三種類型：（1）條件開放型（條件在不斷變化）;（2）結(jié)論開放型（結(jié)論有多個(gè)或結(jié)論無固定）;（3）策略開放型（思維的方法和思維的途徑有多種）.

3? “農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)“閱讀理解”問題，培養(yǎng)學(xué)生的創(chuàng)新能力

【點(diǎn)評(píng)】閱讀理解題主要考查學(xué)生的閱讀能力和對(duì)所學(xué)知識(shí)的整理、歸納能力.閱讀理解題多以新運(yùn)算、新概念、新方法的形式呈現(xiàn).閱讀理解題常見的類型有：（1）閱讀新知識(shí)，解決新問題;（2）閱讀解題過程，模仿解題策略;（3）概括歸納型;（4）閱讀糾正錯(cuò)誤，提高辨別能力[ 1 ].解決這類問題的關(guān)鍵要把握兩點(diǎn)：一是掌握問題原型的特點(diǎn)及解決問題的思想方法;二是根據(jù)問題情境的變化，把握其規(guī)律，領(lǐng)會(huì)問題的本質(zhì)內(nèi)容，合理進(jìn)行思想方法的遷移.[ 2 ]

4? “農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)“方案設(shè)計(jì)型”問題，培養(yǎng)學(xué)生的創(chuàng)新能力

【例題4】某工廠計(jì)劃生產(chǎn)甲、乙兩種機(jī)器共10臺(tái)，其生產(chǎn)成本和利潤(rùn)如表1：

（1）若工廠計(jì)劃獲利14萬元，問甲、乙兩種機(jī)器應(yīng)分別生產(chǎn)多少臺(tái)？

（2）若工廠投入資金不多于44萬元，且獲利多于14萬元，問工廠有哪幾種生產(chǎn)方案？并說明哪種方案獲利最大？最大利潤(rùn)是多少？

【簡(jiǎn)析】（1）根據(jù)“工廠計(jì)劃生產(chǎn)甲、乙兩種機(jī)器共10臺(tái)和工廠計(jì)劃獲利14萬元”，建立方程組求解即可得出結(jié)論;（2）根據(jù)“工廠投入資金不多于44萬元，且獲利多于14萬元”，建立不等式組即可得出結(jié)論.本題主要考查了二元一次方程組、一元一次不等式組的應(yīng)用，正確找出相等關(guān)系和不等關(guān)系是解本題的關(guān)鍵.

【答案】（1）甲、乙兩種機(jī)器應(yīng)分別生產(chǎn)6臺(tái)和4臺(tái);（2）方案一：甲種機(jī)器生產(chǎn)3臺(tái)，乙種機(jī)器生產(chǎn)7臺(tái)，獲利17萬元;方案二：甲種機(jī)器生產(chǎn)4臺(tái)，乙種機(jī)器生產(chǎn)6臺(tái)，獲利16萬元;方案三：甲種機(jī)器生產(chǎn)5臺(tái)，乙種機(jī)器生產(chǎn)5臺(tái)，獲利15萬元.所以方案一獲利最大，最大利潤(rùn)為17萬元.

【點(diǎn)評(píng)】方案設(shè)計(jì)型問題是通過實(shí)例，提出解決問題的要求，讓學(xué)生尋求恰當(dāng)?shù)慕鉀Q方案.這類題型一方面考查了學(xué)生的探究意識(shí)和創(chuàng)新精神，另一方面考查了學(xué)生的實(shí)踐能力.方案設(shè)計(jì)型題涉及生產(chǎn)生活的方方面面，如購(gòu)物、生產(chǎn)配料、汽車調(diào)配、圖形拼接等，所用到的數(shù)學(xué)知識(shí)有方程、不等式、函數(shù)等，即能夠針對(duì)不同的實(shí)際問題，通過建立數(shù)學(xué)模型，把實(shí)際問題轉(zhuǎn)化為數(shù)學(xué)問題，選擇最優(yōu)方案[ 2 ].解答此類題要注重綜合運(yùn)用轉(zhuǎn)化、數(shù)形結(jié)合、方程函數(shù)及分類討論等數(shù)學(xué)思想.

5? “農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)“探究型”問題，培養(yǎng)學(xué)生的創(chuàng)新能力

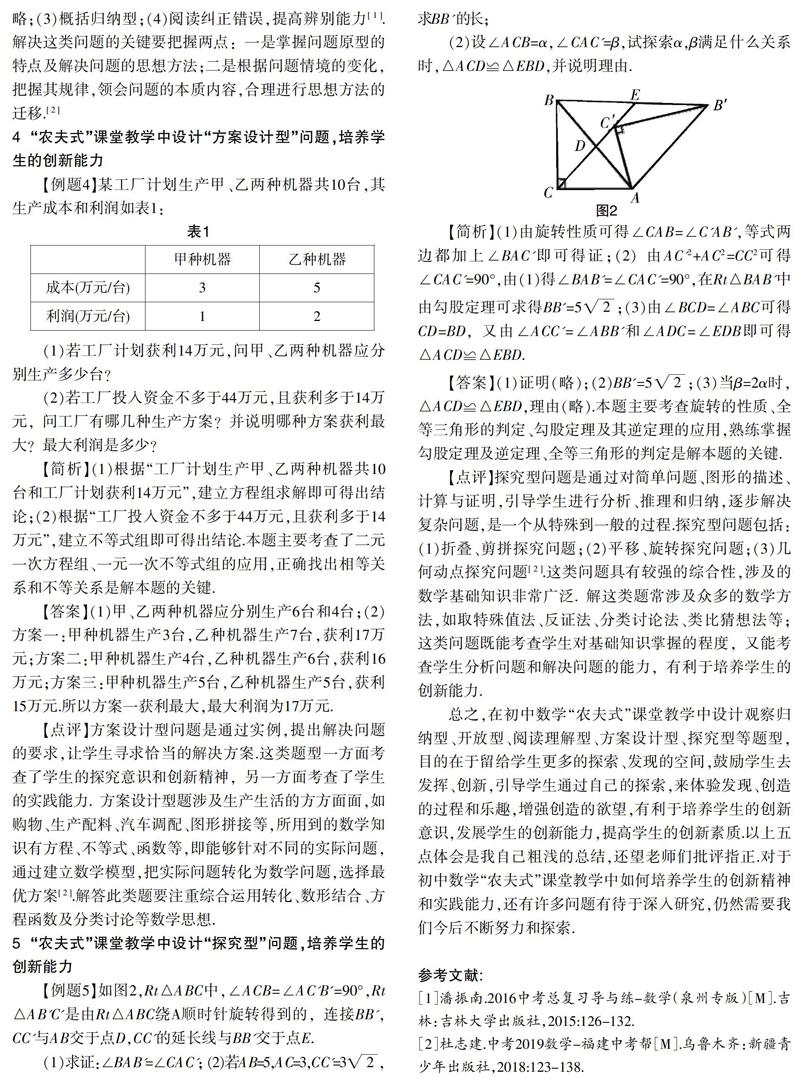
【例題5】如圖2，Rt△ABC中，∠ACB=∠AC'B'=90°，Rt△AB'C'是由Rt△ABC繞A順時(shí)針旋轉(zhuǎn)得到的，連接BB'，CC'與AB交于點(diǎn)D，CC'的延長(zhǎng)線與BB'交于點(diǎn)E.

（2）設(shè)∠ACB=α，∠CAC'=β，試探索α，β滿足什么關(guān)系時(shí)，△ACD≌△EBD，并說明理由.

【點(diǎn)評(píng)】探究型問題是通過對(duì)簡(jiǎn)單問題、圖形的描述、計(jì)算與證明，引導(dǎo)學(xué)生進(jìn)行分析、推理和歸納，逐步解決復(fù)雜問題，是一個(gè)從特殊到一般的過程.探究型問題包括：（1）折疊、剪拼探究問題;（2）平移、旋轉(zhuǎn)探究問題;（3）幾何動(dòng)點(diǎn)探究問題[ 2 ].這類問題具有較強(qiáng)的綜合性，涉及的數(shù)學(xué)基礎(chǔ)知識(shí)非常廣泛.解這類題常涉及眾多的數(shù)學(xué)方法，如取特殊值法、反證法、分類討論法、類比猜想法等;這類問題既能考查學(xué)生對(duì)基礎(chǔ)知識(shí)掌握的程度，又能考查學(xué)生分析問題和解決問題的能力，有利于培養(yǎng)學(xué)生的創(chuàng)新能力.

總之，在初中數(shù)學(xué)“農(nóng)夫式”課堂教學(xué)中設(shè)計(jì)觀察歸納型、開放型、閱讀理解型、方案設(shè)計(jì)型、探究型等題型，目的在于留給學(xué)生更多的探索、發(fā)現(xiàn)的空間，鼓勵(lì)學(xué)生去發(fā)揮、創(chuàng)新，引導(dǎo)學(xué)生通過自己的探索，來體驗(yàn)發(fā)現(xiàn)、創(chuàng)造的過程和樂趣，增強(qiáng)創(chuàng)造的欲望，有利于培養(yǎng)學(xué)生的創(chuàng)新意識(shí)，發(fā)展學(xué)生的創(chuàng)新能力，提高學(xué)生的創(chuàng)新素質(zhì).以上五點(diǎn)體會(huì)是我自己粗淺的總結(jié)，還望老師們批評(píng)指正.對(duì)于初中數(shù)學(xué)“農(nóng)夫式”課堂教學(xué)中如何培養(yǎng)學(xué)生的創(chuàng)新精神和實(shí)踐能力，還有許多問題有待于深入研究，仍然需要我們今后不斷努力和探索.

參考文獻(xiàn)：

[1]潘振南.2016中考總復(fù)習(xí)導(dǎo)與練-數(shù)學(xué)（泉州專版）[M].吉林：吉林大學(xué)出版社，2015：126-132.

[2]杜志建.中考2019數(shù)學(xué)-福建中考幫[M].烏魯木齊：新疆青少年出版社，2018：123-138.