基于卡爾曼濾波器的半捷聯導引頭控制系統設計

韓宇萌,賈曉洪

(中國空空導彈研究院， 河南 洛陽 471009)

在現代戰爭中，精確制導武器已成為最主要和最有效的攻防手段，紅外制導空空導彈由于具有制導精度高、目標識別能力強、隱蔽性好等優點，成為空戰近距格斗不可或缺的精確制導武器[1]。近距格斗中紅外導引頭的主要作用是對目標進行自主搜索、自動識別、快速捕獲和精確跟蹤。目前紅外型空空導彈已經發展到第四代，以滾仰式兩軸框架結構和紅外成像制導技術為標志，具有較強的目標識別能力和較高的制導精度。滾仰式兩軸框架結構減小了導引頭的體積，增大了導引頭的跟蹤場和隨動范圍。其小型化對改進導彈氣動性能、提高射程具有重要的現實意義，大跟蹤場和隨動范圍對擴大發射區實現越肩跟蹤、降低載機機動占位等方面具有重要的現實意義[2-3]。滾仰式兩軸半捷聯導引頭是第四代紅外空空導彈的理想選擇，美國研制的AIM-9X是其中的典型代表。

1 導引頭控制現狀分析

隨著光電對抗技術的不斷發展，在現代戰爭中，沒有人工干擾的凈空作戰條件已經不復存在。紅外空空導彈在鎖定并攻擊目標的過程中，各種紅外有源干擾和目標逃逸相互交織，對紅外導引頭目標識別和穩定跟蹤造成嚴重影響[1,4]。同時，近距格斗中導彈高速飛行時的大過載、高機動使得彈體姿態處在復雜變化中，再加上導彈外部氣流的擾動，對導引頭的目標跟蹤和穩定控制造成嚴重影響。為了提高導引頭控制系統的動態響應性能和跟蹤精度，國內外學者進行了大量的研究。目前，導引頭控制器設計大部分應用的是傳統的PID控制算法[5]。PID控制器結構簡單，對信號具有較好的控制作用，能使系統快速收斂到平穩狀態，應用廣泛。但PID控制效果依賴于模型，對控制擾動和噪聲的處理能力不足，其控制器參數的選擇對控制效果影響較大。為了提高導引頭穩定平臺的抗擾動能力和跟蹤精度，諸多控制算法被應用于導引頭控制系統中。如滑模控制方法被應用到導引頭控制器設計中，它能夠有效隔離彈體擾動，提高導引頭的跟蹤精度和控制魯棒性[6-8]。采用神經網絡的導引頭控制策略，一般是通過對控制系統性能的自適應學習，實現PID控制器參數的最佳組合從而得到理想的控制效果，但這種神經網絡自適應學習控制策略，其參數整定過程繁瑣、算法復雜，實際應用中計算的實時性難以滿足要求[9]。

卡爾曼濾波對控制干擾和測量噪聲具有良好的濾波作用[10]，本文針對滾仰式半捷聯導引頭提出了一種基于目標狀態估計的卡爾曼濾波方法應用于導引頭控制，該方法結合了卡爾曼濾波器在濾除干擾噪聲方面的良好性能，能夠使滾仰式半捷聯導引頭在外部擾動和系統噪聲的作用下保持對運動目標的精確跟蹤。

2 導引頭控制原理

滾仰式半捷聯導引頭具有滾轉和俯仰兩個自由度，其光學系統安裝在穩定平臺框架上，穩定平臺內外框架在各框架力矩電機驅動下可繞相應框架軸轉動[11]。導引頭控制系統在設計時，首先根據穩定平臺的外形尺寸和性能要求，制定系統的基本控制方案，然后選擇系統主要元器件，最后建立數學模型分析系統動態響應，并根據期望的性能指標設計調節器。穩定平臺由臺體、傳動機構、力矩電機、驅動功放、校正網絡、角度傳感器、角速度傳感器等構成[12-13]。其控制回路多采用位置-速度雙回路控制系統，其中位置回路主要用來提高控制系統的精度，速度回路主要用來減小控制系統的超調量，改善回路的動態性能，以滿足系統的穩態和動態要求。滾仰式半捷聯導引頭控制原理框圖如圖1。

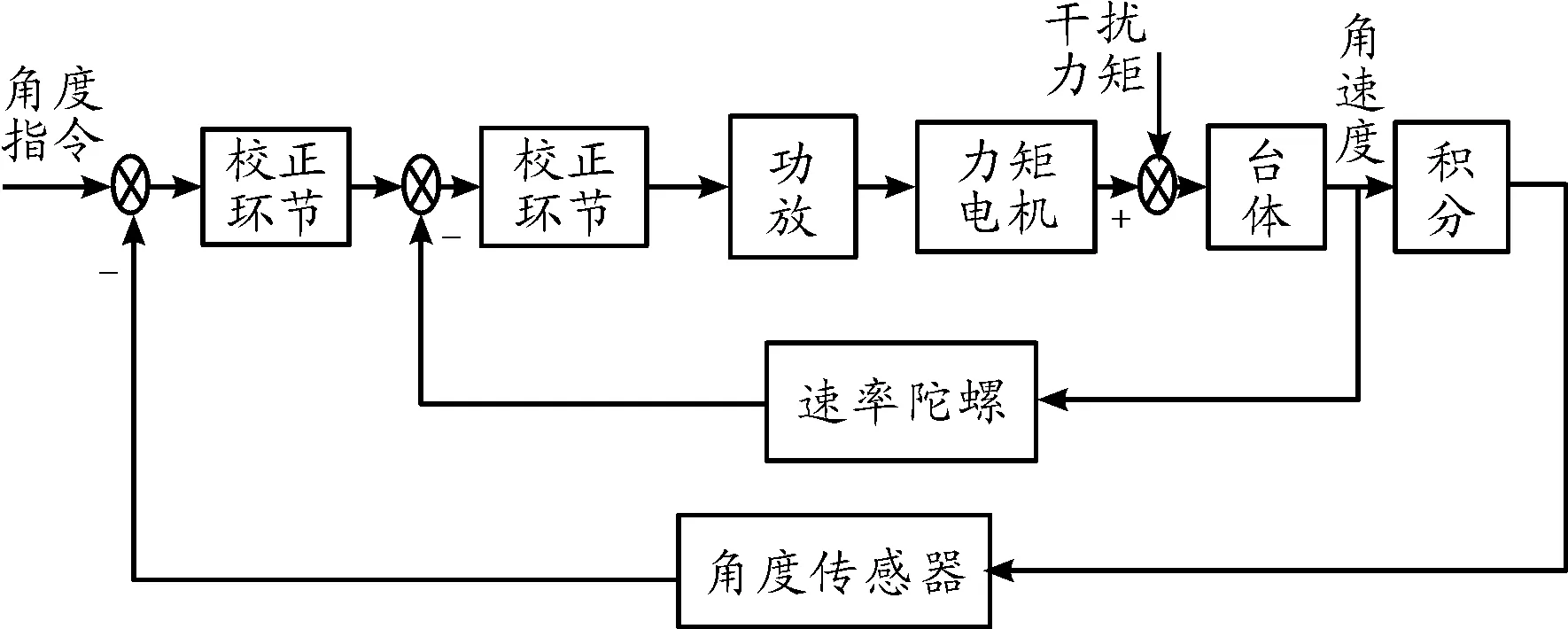
圖1 導引頭控制系統原理框圖

滾仰式半捷聯導引頭穩定平臺的主要功能是保持導引頭光軸穩定，隔離彈體擾動，對目標實現精確跟蹤。當彈體姿態劇烈變化或導引頭受到外界擾動時，圖像系統輸出的失調角有可能會出現跳動現象，進而影響導引頭跟蹤的穩定性。為避免這種影響，導引頭控制系統應該具有較高的跟蹤精度和穩定精度、具有對目標的快速跟蹤能力，其控制器的設計和控制策略的選擇是實現導引頭功能的關鍵所在。同時為實現對目標的精確制導，要求導引頭必須具備良好的控制性能以確保交會過程中對目標快速穩定跟蹤。

3 基于卡爾曼濾波的導引頭控制

3.1 卡爾曼濾波原理

卡爾曼濾波算法中利用到了系統狀態方程、量測方程、測量誤差的統計特性和白噪聲激勵的統計特性等，卡爾曼濾波本質是遞推無偏線性最小方差估計，估計結果在線性估計中精度最佳[10]，下面簡單介紹下卡爾曼濾波原理。

設系統的狀態方程為

Xk=Φk,k-1Xk-1+Γk,k-1Wk-1

(1)

設系統的量測方程為

Zk=HkXk+Vk

(2)

其中:Xk為狀態向量，Xk-1為上一時刻的狀態向量，Φk,k-1為狀態轉移矩陣，Γk,k-1為過程噪聲輸入矩陣，Wk-1為過程噪聲序列，Zk為量測值，Hk為量測矩陣，Vk為測量噪聲序列。

若滿足式(1)和式(2)的線性隨機系統的過程噪聲和量測噪聲為高斯白噪聲且它們不相關，則可得到下述卡爾曼濾波方程。

比較兩組的手術時間、術中出血量和手術費用。采用日本骨科協會評分（JOA評分）評估患者神經功能，改善率計算方式如下：神經功能改善率=（治療后JOA評分-治療前JOA評分）/（17-治療前評分）×100%。

1) 狀態一步預測方程：

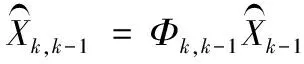
(3)

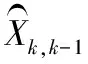
2) 一步預測均方誤差：

(4)

其中:Pk,k-1為狀態預測的均方誤差矩陣，Qk-1為過程噪聲方差。

3) 濾波增益：

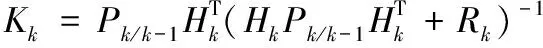
(5)

其中Rk為量測噪聲方差陣。

4) 狀態估計方程:

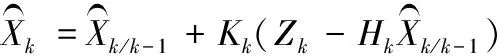
(6)

Pk=(I-KkHk)Pk/k-1

(7)

式(3)～式(7)即為離散形式的卡爾曼濾波基本方程，該濾波方法能夠在線性高斯模型條件下，對目標狀態做出最優估計[10]。

3.2 導引頭狀態方程與量測模型

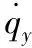
圖2 慣性坐標系和視線坐標系的關系

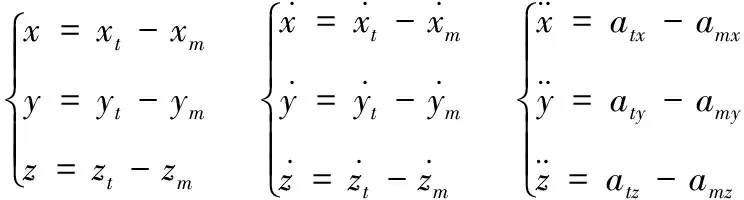
(8)

假設目標為常加速度運動模型，把目標的加加速度作為隨機白噪聲處理，可得：

(9)

wx、wy、wz為高斯白噪聲，則導引頭的狀態方程可表示為

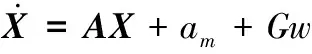
(10)

由于導彈自身加速度可量測，式(10)中導彈加速度am為已知輸入量。因此在慣性坐標系下導引頭的狀態方程是線性的，其中：

由圖2慣性坐標系與視線坐標系的位置關系可得：

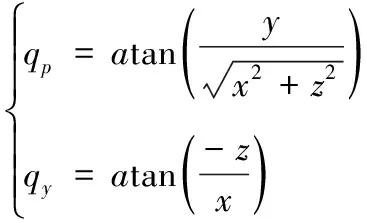
(11)

根據導引頭框架角、圖像失調角等可以得到彈目視線角，因此導引頭量測方程為

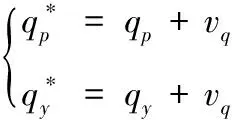
(12)

根據導引頭狀態方程和量測方程，可采用卡爾曼濾波器進行目標運動狀態估計，實現對半捷聯導引頭的穩定控制與快速跟蹤。

4 仿真分析

根據滾仰式半捷聯導引頭穩定與跟蹤原理，采用基于目標運動狀態估計的卡爾曼濾波方法對導引頭進行控制，導引頭控制仿真模型如圖3所示。其中PID控制器的參數設置為kp=10、ki=1、kd=1，取采樣時間為1 ms。設導引頭控制干擾信號其均值為0度，方差為0.02。設導引頭探測器測量值的偏差其均值為0度，方差為0.02。

為了評估半捷聯導引頭采用卡爾曼濾波方法對運動目標的跟蹤效果，給系統輸入正弦激勵信號u=sin(2πt)。理想信號及帶有噪聲的信號如圖4所示、理想信號及濾波后的信號如圖5所示。從圖5中可以看到，卡爾曼濾波方法對控制干擾和測量噪聲具有良好的濾波作用，導引頭控制系統的響應結果很好的復現了期望的軌跡，控制誤差接近于0。

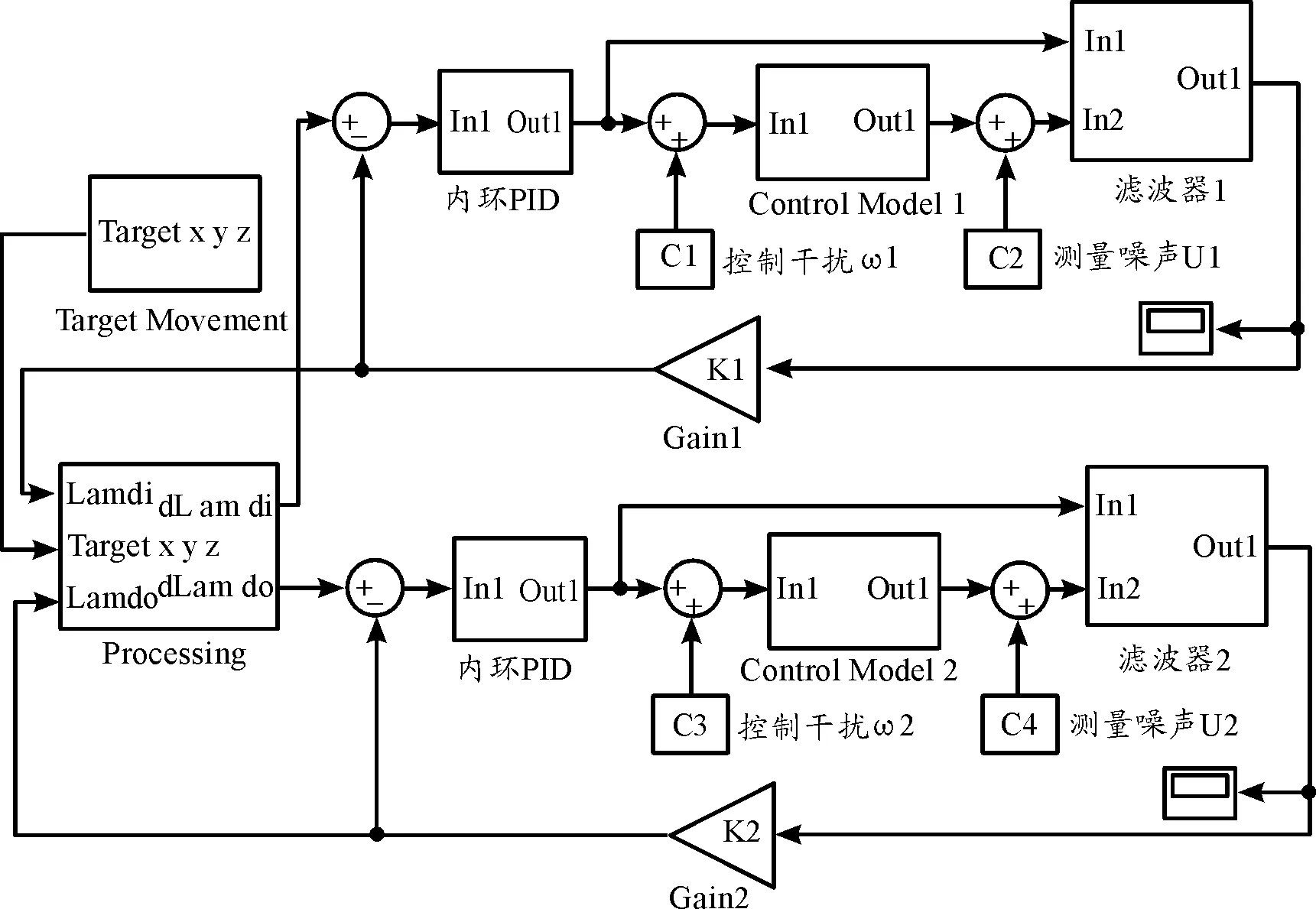
圖3 滾仰式半捷聯導引頭控制仿真模型示意圖

圖4 理想信號及帶有噪聲的信號

圖5 理想信號及濾波后的信號

從以上仿真結果可以看出：基于目標運動狀態估計的卡爾曼濾波方法應用于半捷聯導引頭控制系統，對控制干擾和測量噪聲具有良好的濾波作用，能夠有效提高導引頭控制系統的魯棒性。

為了進一步驗證該控制算法的性能，在半捷聯導引頭穩定與跟蹤一體化仿真模型中，假設目標的運動方程為x(t)=8 000，y(t)=2 000+300*sin(0.5t)，z(t)=2 000+300*cos(0.5t)。設導引頭控制干擾信號其均值為0度，方差為0.02。設導引頭探測器測量值的偏差其均值為0度，方差為0.02的白噪聲。考察在噪聲作用下滾仰式半捷聯導引頭對運動目標的跟蹤性能。由圖6、圖7可知：在干擾信號和測量噪聲作用下滾仰式半捷聯導引頭可始終保持對目標的穩定跟蹤，跟蹤誤差可控制在2個像素以內。運動目標在滾仰式半捷聯導引頭瞬時視場內的軌跡如圖8所示，可以看出目標始終在導引頭瞬時視場內。基于目標運動狀態估計的卡爾曼濾波方法能夠使滾仰式半捷聯導引頭在擾動和噪聲作用下保持對運動目標持續穩定的跟蹤。

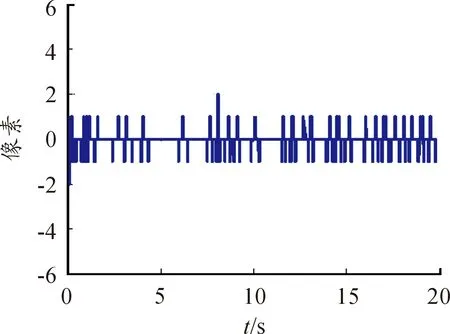
圖6 X向導引頭跟蹤誤差

圖8 導引頭瞬時視場中目標運動軌跡

5 結論

本文提出的基于目標運動狀態估計的卡爾曼濾波方法應用于半捷聯導引頭控制，使導引頭對控制干擾和測量噪聲具有良好的濾波作用，能夠有效提高導引頭控制系統的魯棒性。仿真結果表明，采用基于目標運動狀態估計的卡爾曼濾波方法應用于導引頭控制，能夠使導引頭控制回路的自適應能力得到提高，能夠使導引頭在干擾和噪聲作用下實現對運動目標的穩定跟蹤，為滾仰式半捷聯導引頭的控制系統設計提供參考。