吊掛橫梁螺栓拉力計算結果差異性分析
林海彬,陳 雷,孫英超,2,朱利媛,毛端華
(1.航空工業洪都 導彈設計所,南昌 330024;2.哈爾濱工程大學 航天與建筑工程學院,哈爾濱 150001)
吊掛橫梁是導彈上一個重要的連接結構件,作為導彈與發射架連接的機械接口,要滿足導彈掛機飛行過程中各種沖擊、振動、過載等苛刻的工作條件。吊掛橫梁通過螺栓和定位銷與彈身連接,螺栓傳遞彈體產生的拉力載荷,定位銷傳遞彈體產生的剪力載荷,有必要在組合加載載荷下對各個螺栓的受力進行計算[1-3]。吊掛橫梁連接結構研究文獻很少,多見類似吊掛橫梁的端板連接結構研究,對于端板結構中連接螺栓的載荷計算沒有確定的方法,傳統規范中計算理論僅按抗拉進行驗算,一些文獻認為應按照抗拉和抗彎同時驗算,理論上存在爭議[4]。任艷然等[5]考慮了螺栓屈服后塑性對連接螺栓的拉力影響進行了分析。施剛等[6]對端板連接的剛度和承載力特性進行了試驗研究,認為端板連接大多屬于半剛性連接,在加載載荷作用下,節點發生明顯的轉動變形。趙偉等[7]對外伸端板加勁肋進行了試驗和有限元仿真研究。本文針對國內外關于端板螺栓的螺栓力計算方法進行敘述,確定吊掛橫梁螺栓受力工程計算方法,在單一加載載荷下與有限元計算結果逐一對比,得到了兩種計算方法結果的差異性,可供類似連接結構螺栓受力計算參考。
1 計算模型
計算模型采用導彈掛機著陸的過載,引用彈體局部坐標系Oxyz,原點O為彈身頭部頂點,X軸正方向為導彈逆航向,Y軸在彈身對稱面內向上為正,Z軸方向符合右手法則(順航向向左為正)。吊掛橫梁承受彈體傳遞的3個方向載荷分別為Nx(軸向),Ny(法向),Nz(側向),由于彈體質心與吊掛受力面存在高度差,彈身的側向過載載荷Nz產生彎矩載荷Mx,彈身的軸向過載載荷Nx(軸向)產生的彎矩載荷Mz可分配到前后吊掛的法向載荷Ny中,彈身的法向過載載荷Ny直接分配到前后吊掛的法向載荷Ny中,不產生附加彎矩。三個方向集中力載荷Nx,Ny,Nz和一個彎矩載荷Mx作為載荷輸入。吊掛加載載荷為Ny=130 000 N,Nz=50 000 N,Mx=15 000 000N·mm。吊掛橫梁示意圖如圖1,其中N1,N2,N3,N4,N5,N6為6個連接螺栓的編號,螺栓只承拉力載荷,不傳遞剪力載荷,剪力載荷由位于吊掛橫梁底部的定位銷傳遞,編號為N7。
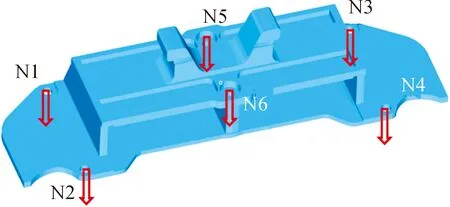
圖1 吊掛模型示意圖
2 工程算法
2.1 彎矩載荷計算
根據傳統的工程估算方法,結構受彎矩載荷時,吊掛橫梁上的螺栓載荷可參考鋼結構梁柱端板計算方法,國內外彎矩載荷計算方法如圖2所示。
國內假設轉動平面為剛體,吊掛橫梁上的螺栓呈線性分布;英國規范按照線彈性方法進行螺栓拉力計算,認為最外兩排螺栓承受相同拉力;歐洲規范按塑性設計,認為相對分布中心最遠端的螺栓受力至最大后,拉力重新分配到下一排螺栓上;美國規范認為彎矩應簡化一對力偶,按照杠桿分配原理確定節點承載力[8-9]。
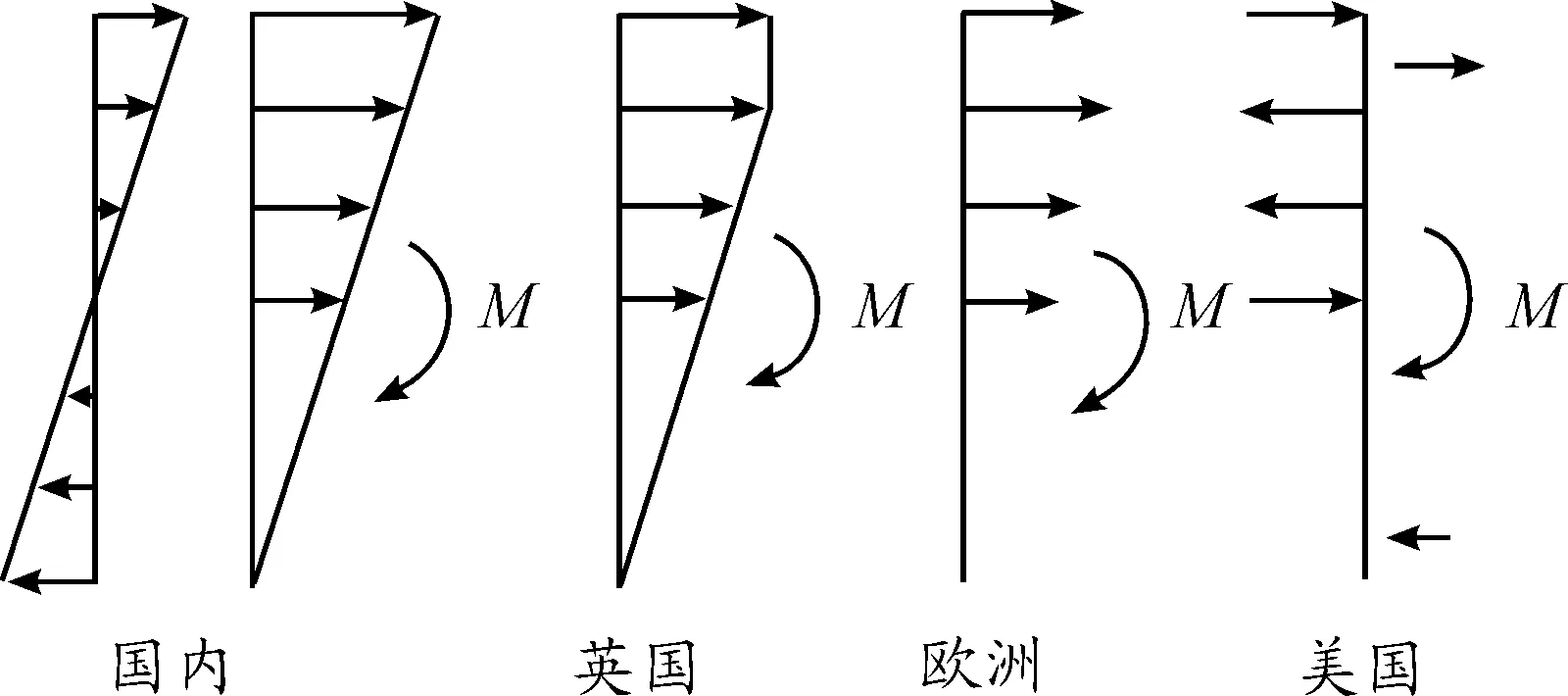
圖2 國內外彎矩載荷計算方法
從上述受力模型看,螺栓組連接載荷分配方法還需進一步完善,設計時采用的計算方法比較保守,與實際受力狀態并不一致。在文獻[10]中提到平齊式連接結構采用平截面假定計算,對于外伸式端板連接,還沒有成熟的改進方案,可認為受拉翼緣兩側螺栓拉力相等,該計算方法與英國規范計算方法類似。
2.2 拉力載荷計算
結構受軸向拉力載荷時,當力作用線通過螺栓組的形心時,吊掛橫梁上的螺栓均參與承載,并且平均分配該載荷。當力作用線不通過螺栓組的形心時,國內工程算法按大小偏心進行區分計算[8-9],并考慮端板效應。其中大小偏心載荷產生的附加彎矩載荷分配方法與吊掛橫梁自身存在的彎矩載荷分配方法相同如下敘述。
當力作用線不通過螺栓組的形心時,有一定偏心距離,如圖3所示。根據螺栓實際受力狀態,螺栓只能承受拉力,不會產生壓力,理論計算時,根據螺栓組位置計算出形心o,認為轉動中心位于該處。F為偏心拉力載荷,e為偏心距離,假設條件如下時:
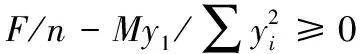
(1)
螺栓最大拉力值為拉力的平均分配值和彎矩分配的值相疊加,最大螺栓受拉力計算結果如下公式所示:
(2)
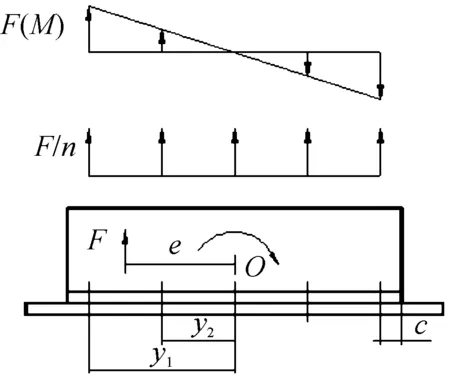
圖3 小偏心載荷分配簡化
螺栓承載計算時需考慮其真實受力狀態,每個螺栓承載狀態為拉力產生正值載荷與彎矩產生的正值或負值載荷相疊加,螺栓承載計算結果會出現負值情況,吊掛橫梁螺栓連接處有一定厚度,螺栓受壓狀態在真實工作中不會出現,需對轉動中心重新定義,認為在最外排螺栓o′處為螺栓組的轉動形心。大偏心載荷分配簡化如圖4所示。
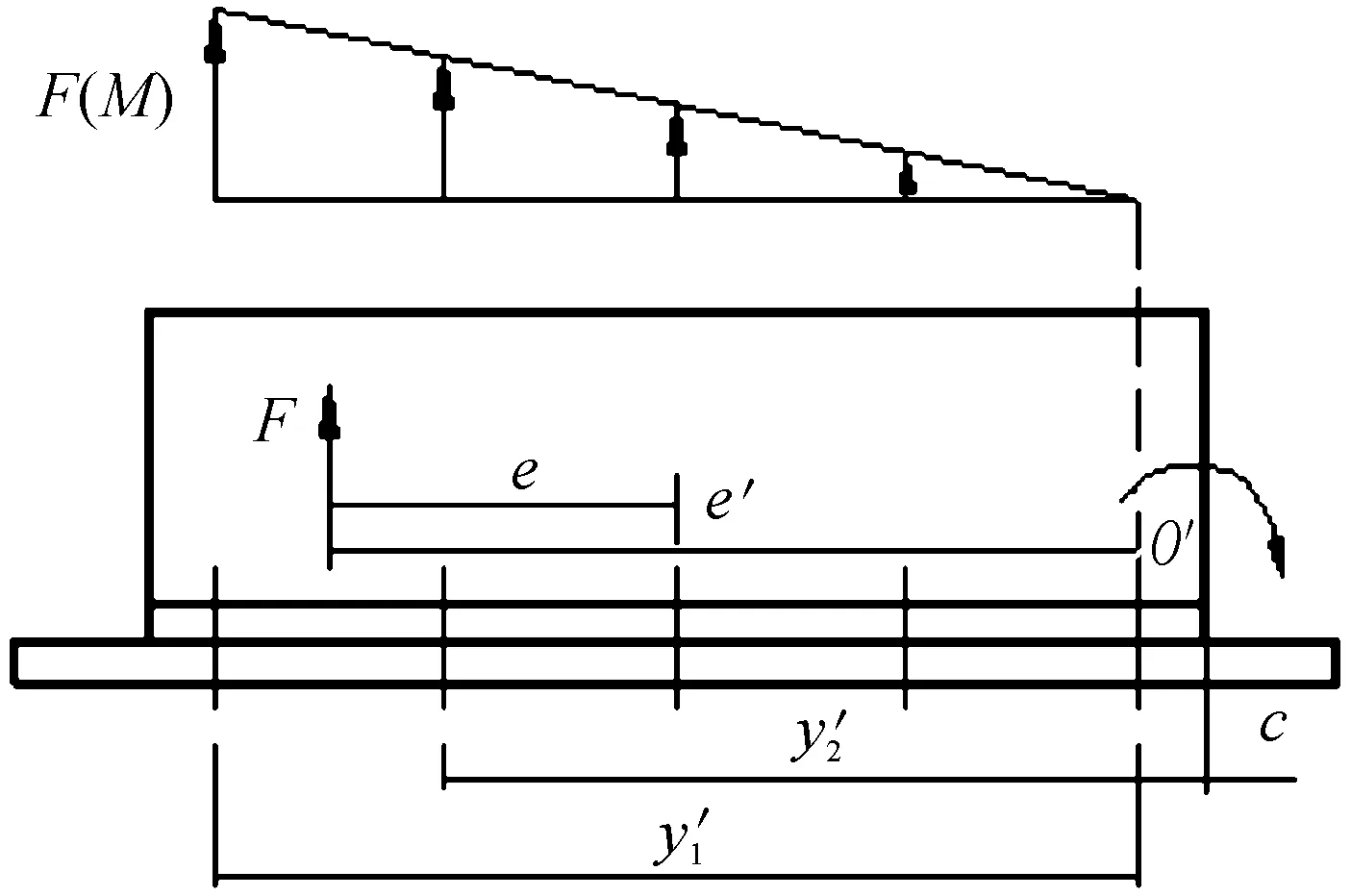
圖4 大偏心載荷分配簡化
F為偏心拉力載荷,e為偏心距離,e′為判別后的偏心距離,c為轉動形心位置最外排螺栓到端板邊界的距離。假設條件如下時:
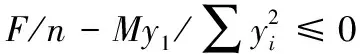
(3)
螺栓最大拉力值為拉力的平均分配值和彎矩分配的值相疊加,最大螺栓受拉力結果如下公式所示:
(4)
由于在最外排螺栓o′處為螺栓組的轉動形心,沒有考慮端面兩板之間受壓,計算內力不平衡,所以計算時需要考慮兩板端面受壓臨界值。需增加判別公式如下:
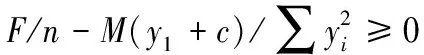
(5)
2.3 吊掛橫梁工程算法
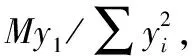

圖5 大偏心載荷分配簡化
3 計算結果對比
3.1 有限元建模
對吊掛橫梁結構建立有限元模型,材料為30CrMnSiA。彈身傳遞的載荷通過MPC單元加載到兩側吊耳上,吊耳加載Y方向力載荷、Z方向力載荷、X方向彎矩載荷。
有限元軟件中模擬螺栓、螺釘常見的單元為彈簧單元、梁單元、桿單元[11-16]。在ABAQUS有限元軟件中還提供了fastener單元,該單元采用基于獨立網格技術,可通過空間任意一點或多點沿指定方向被連接件的釘孔處投影而創建,無需人工操作使其與被連接件模型的網格節點一一對應。Fastener單元采用Bushing連接屬性,該連接屬性允許被連接的兩個節點在局部三維笛卡爾坐標系下相對獨立運動。對于非耦合線彈性的Bushing連接屬性具有6個自由度,其屬性如圖6所示,均遵循胡克定律:
Fi=Diiuii(i=1,2,…,6)
(6)
式中:uii表示局部坐標系下的自由度i方向的位移或轉角;Dii表示自由度i方向的等效彈簧剛度;Fi表示連接單元在自由度i方向所受的力或矩。
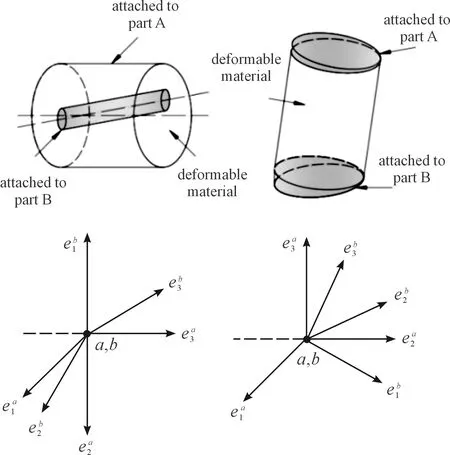
圖6 BUSH單元6自由度屬性
3.2 工程算法和有限元結果
有限元軟件計算時,對螺栓連接分別采用BUSH單元、ROD單元、MPC單元模擬,表1給出了連接螺栓分布位置及載荷分配系數,表2給出了工程算法計算結果和不同模擬螺栓單元的有限元計算結果,其中負載荷表示螺栓受壓載荷。

表1 螺栓空間位置及分配系數
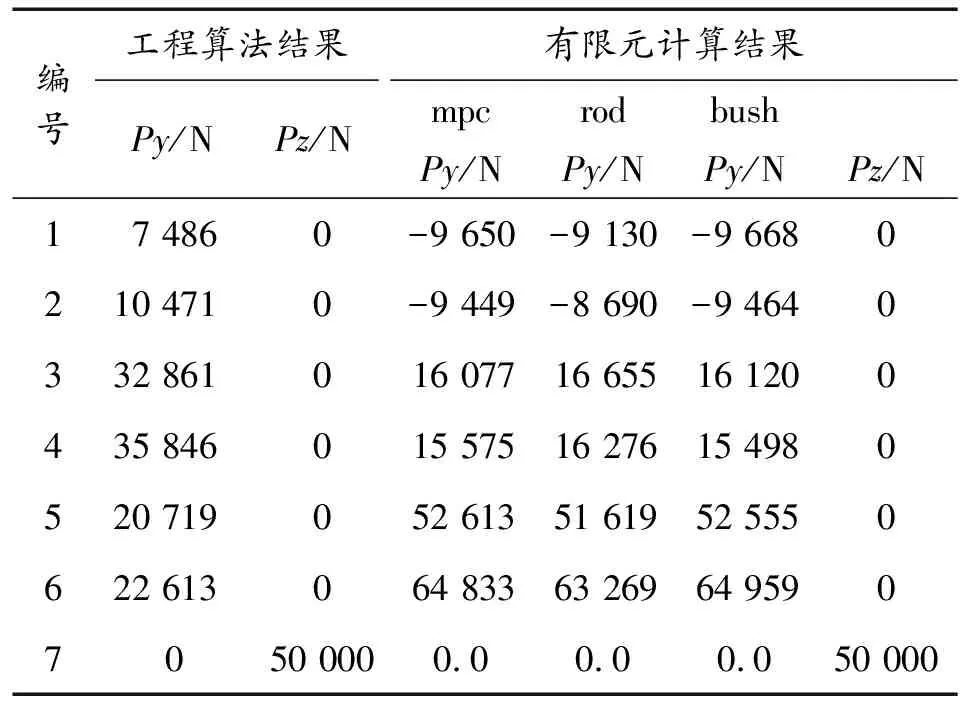
表2 兩種算法計算結果
從表2可以看出,在組合加載載荷下螺栓計算的結果有明顯差異。為了找出計算結果差異,將組合載荷拆分成單一載荷,單一載荷分別為拉力載荷、彎矩載荷、側向載荷,在單一載荷下,對工程算法計算結果和不同模擬螺栓單元的有限元計算結果進行對比,計算結果如表3~表5。

表3 拉力載荷下計算結果
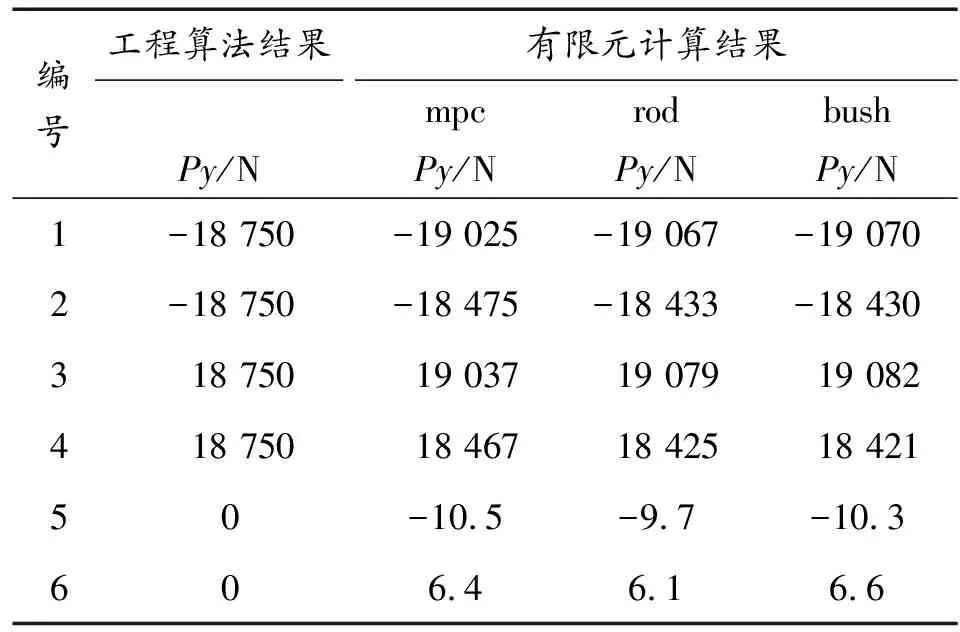
表4 彎矩載荷下計算結果
從表3~表5計算結果對比可以得到,在彎矩加載載荷、側向加載載荷下,兩種計算方法得到的6個螺栓的受力值比較接近。在拉力加載載荷下,兩種計算方法得到的6個螺栓受力值存在差異。在工程算法計算時,只根據螺栓空間分布位置和載荷空間位置對各個螺栓進行載荷計算,沒有考慮內部結構對結果的影響,有限元仿真計算時,以實際結構建模進行仿真分析,載荷按結構剛度和傳力路徑的長短來分配。
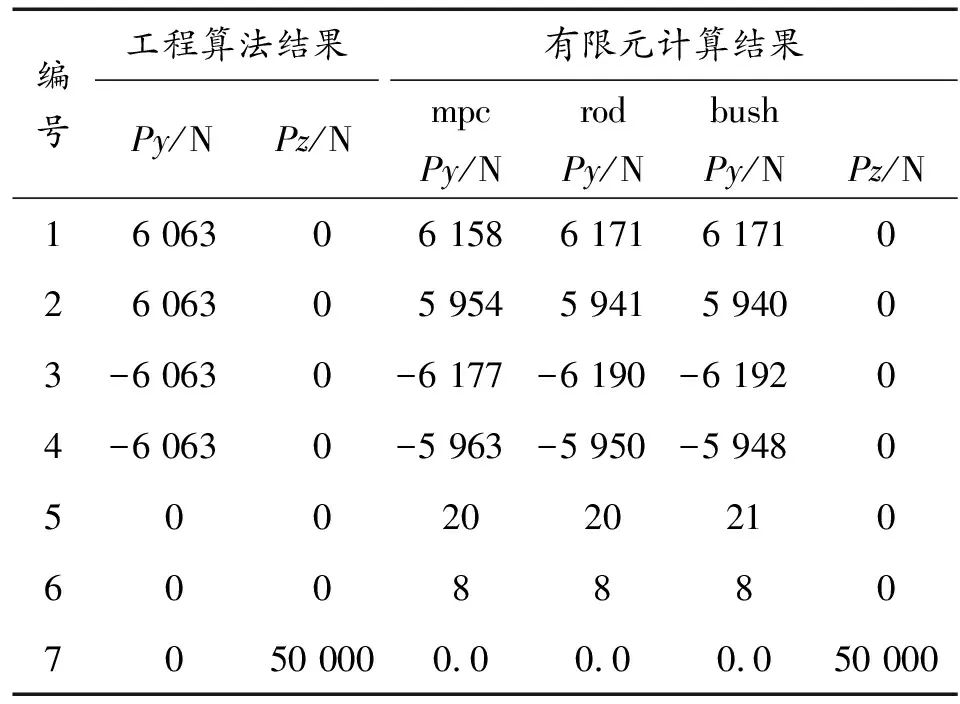
表5 側向載荷下計算結果對比
3.3 有限元驗證模型
為了驗證拉力載荷下,不同內部結構對載荷傳遞的影響,建立簡化有限元模型,采用桿元模擬螺栓連接,模型見圖7所示,該模型保留吊掛橫梁螺栓孔位置和載荷加載的位置。
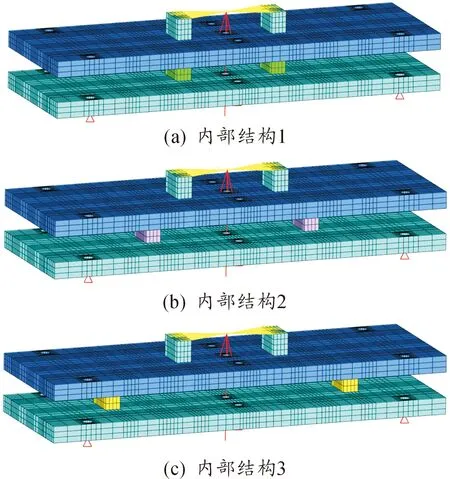
圖7 有限元簡化模型
3種簡化有限元模型內部連接支撐位置不同,相對應計算模型描述為內部結構1、內部結構2、內部結構3,對相同加載載荷下各螺栓受拉力的計算結果如表6所示。
對比3個有限元計算模型結果,各個螺栓分配的載荷存在差異,該差異性是工程算法無法得到的。對內部結構1模型,由于連接支撐位置靠近中間兩個連接螺栓,所以中間編號為N5、N6的螺栓分配載荷多于其余四個螺栓的載荷分配。對內部結構2模型,由于連接支撐位置在最外端螺栓和中間螺栓中間,N5、N6螺栓會進行兩次載荷分配疊加,進而分配載荷大于兩側螺栓分配的載荷。對內部結構3模型,由于連接支撐位置靠近最外端連接螺栓位置,N5、N6螺栓分配的載荷小于兩側螺栓分配的載荷。
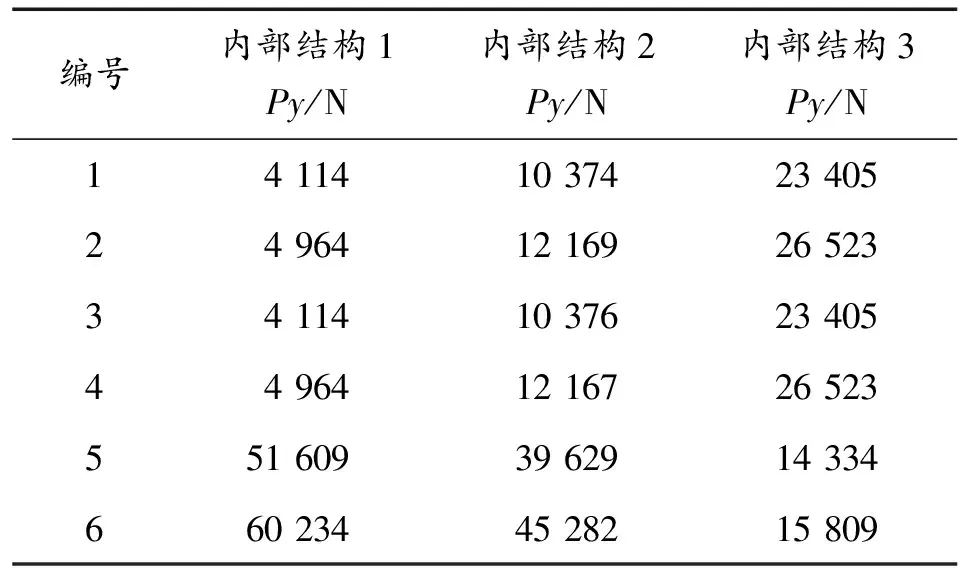
表6 3種有限元簡化模型計算結果
4 結論
1) 對吊掛橫梁結構的螺栓分配的載荷分別進行了工程算法和有限元仿真兩種方法計算,計算結果存在差異。有限元計算時采用了BUSH單元、桿元,MPC單元模擬螺栓,得到的螺栓拉力結果基本無差異。
2) 對組合載荷拆分成單一載荷加載,拉力加載載荷下螺栓承載結果存在差異,彎矩加載載荷、側向加載載荷下兩種計算方法得到的螺栓承載結果一致。
3) 對連接結構簡化成3種不同的有限元模型,從有限元計算結果中看出加載位置和約束位置相同情況下,螺栓計算結果與連接結構的內部結構有關,不同的內部結構對傳力路線和連接結構剛度有影響。
4) 螺栓載荷計算時,假定連接結構剛度無限大,忽略內部結構差異的影響,可采用工程算法。如內部結構對螺栓計算結果影響很大時需考慮有限元仿真計算方法。
5) 橫梁結構有限元計算結果相對于工程算法計算結果更符合螺栓實際受力狀態。由于螺栓受力需要考慮材料彈塑性,當某一螺栓分配載荷達到某一值時,其他螺栓上的載荷會重新分配,并需考慮接觸邊界的變化和載荷疊加對轉動中心或中性軸假設的影響。

