Markov-Hurwitz 型方程研究

上海市世界外國(guó)語(yǔ)中學(xué) 熊浩明

定義1：我們稱x2+y2+z2=kxyz為Markov 方程（其中k是正整數(shù)），有以下結(jié)論：

定理1：如果Markov 方程有正整數(shù)解，那么k≤3。

具體地，當(dāng)k=1，3 時(shí)，有正整數(shù)解；而當(dāng)k=2 時(shí)，沒(méi)有正整數(shù)解。

事實(shí)上，我們有更一般的結(jié)果：

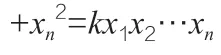
一、主要結(jié)果

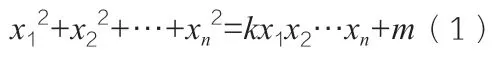
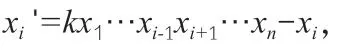
定義4：如果通過(guò)韋達(dá)變換使得方程（1）的正整數(shù)解(x1，x2，…，xi，…，xn）→(x1，x2，…，xi'，…，xn），對(duì)1 ≤i≤n，其中xi'=kx1…xi-1xi+1…xn-xi＞0，則稱(x1，x2，…，xi，…，xn）與(x1，x2，…，xi'，…，xn）是等價(jià)的。

對(duì)Markov-Hurwitz 方程所有等價(jià)的解記為某個(gè)等價(jià)類，即相同等價(jià)類中的兩個(gè)解可以通過(guò)一系列的韋達(dá)變換得到，而不同等價(jià)類中的解是無(wú)法通過(guò)韋達(dá)變換得到的。如果一個(gè)正整數(shù)解通過(guò)韋達(dá)變換無(wú)法得到另一個(gè)正整數(shù)解，則它本身構(gòu)成一個(gè)等價(jià)類。在每個(gè)等價(jià)類中，我們記最小的那個(gè)解為極小解（即各變量的和為最小，但未必唯一）。如果有s個(gè)等價(jià)類，那么就有s個(gè)極小解。極小解也稱為基本解，各個(gè)不同的基本解是無(wú)法通過(guò)韋達(dá)變換轉(zhuǎn)化的。

如果令0 ＜x1≤x2≤…≤xn，當(dāng)k≥2 時(shí)，由韋達(dá)變換的定義，我們發(fā)現(xiàn)一般的韋達(dá)變換會(huì)將解的各變量的和增大，除非i=n，即變換xn'=kx1x2…xn-1-xn，它是唯一可能使解減小的變換。我們得到如下的重要結(jié)果：

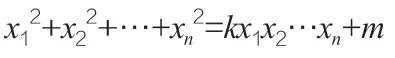
二、定理的證明

首先我們給出定理2 的證明。

定理2：對(duì)n≥3，k為給定正整數(shù)，如果不定方程x12+x22+…+=kx1x2…xn有正整數(shù)解，那么k≤n。

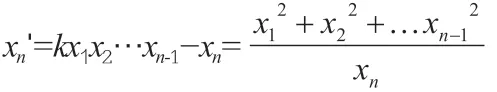
如果xn=1，那么x1=x2=…=xn=1，這就得到k=n。

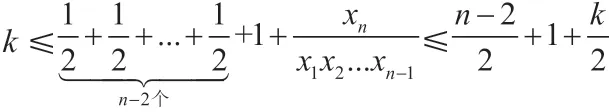
即得k≤n。

所以我們證明了定理2。

定理3 是本文的核心定理。接著給出定理3 的證明：

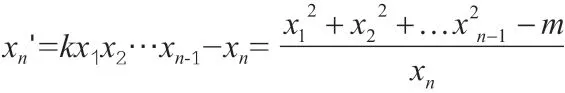
所謂“醫(yī)養(yǎng)結(jié)合”就是指將醫(yī)療資源與養(yǎng)老資源結(jié)合起來(lái)，實(shí)現(xiàn)資源效率的最大化，使養(yǎng)老機(jī)構(gòu)既具有養(yǎng)老功能又具有醫(yī)療功能，是一種把生活照料與醫(yī)療服務(wù)融為一體的新型養(yǎng)老模式。然而，廣西在“醫(yī)養(yǎng)結(jié)合”工作方面進(jìn)展緩慢，地方政府及相關(guān)部門沒(méi)有按照“醫(yī)養(yǎng)結(jié)合”的本質(zhì)要求來(lái)研究和制訂實(shí)施方案，因此，包括營(yíng)利性養(yǎng)老服務(wù)機(jī)構(gòu)在內(nèi)的廣西各類養(yǎng)老服務(wù)機(jī)構(gòu)的“醫(yī)養(yǎng)結(jié)合”工作沒(méi)有太大起色。

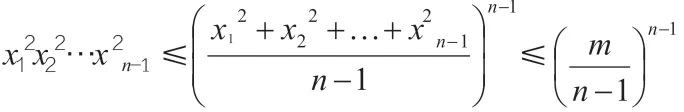
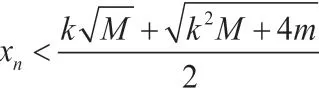
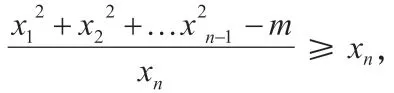
這就證明了基本解的個(gè)數(shù)是有限個(gè)，即存在一個(gè)基本解的有限集合{A1，A2，…，As}，方程的所有解都可以由這個(gè)集合中的元素生成。

我們現(xiàn)在對(duì)k=1,2 的情況作些說(shuō)明，這時(shí)的方程有可能出現(xiàn)無(wú)限多組基本解：

（1）如果k=2，更細(xì)致地分析上述不等式（＊）：

當(dāng)xn-2=1 時(shí)，此時(shí)方程成為x2+y2+n-2=2xy+m，即（x-y）2=m+2-n，令m+2-n=s2，則xn=a+s,xn-1=a是最小解，如果s＞0，由于韋達(dá)變換將（a，a+s）→（a+2s，a+s），所以基本解為（1，…，1，1+s）,（1，…，1，2，2+s，），…，（1，…，1，s，2s）這s組；如果s=0，那么(x，y)=(a，a)無(wú)法通過(guò)韋達(dá)變換互相得到，此時(shí)原方程有無(wú)窮多組基本解：(1，…，1，a,a)。

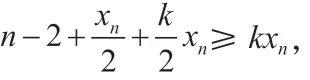
當(dāng)xn-2=2，且x1=x2=…=xn-3=1 時(shí)，原方程變?yōu)椋簒2+y2+n+1=2xy+m，即（x-y）2=m-n-1，當(dāng)m=n+1 時(shí)，x=y=a，此方程的基本解為(1，…，1，2，a,a)，為無(wú)限多組，當(dāng)m-n-1=s2＞0 時(shí)，此方程的基本解為(1，…，1，2，a,a+s)，a=1,2,…，s，共s組。

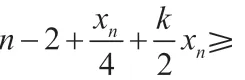
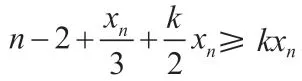
上述分析指出，只有在k=2，m=n-2 時(shí)或者k=1，m=n+1 時(shí)，方程存在一組無(wú)限的基本解，其余情況方程的基本解都是有限組，我們可以得到如下的結(jié)果：

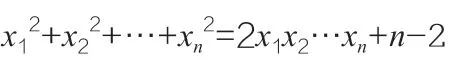
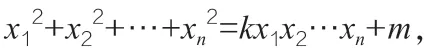
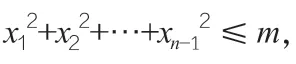
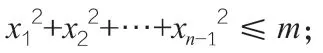
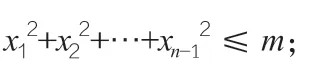
注：當(dāng)m＞0 時(shí)，上述xn的不等式是嚴(yán)格的，即等號(hào)不成立。

實(shí)踐證明，當(dāng)n不太大時(shí)，這種方法是有效的，而在m不是很大時(shí)，我們甚至還能證明某些方程無(wú)解。但對(duì)k=1 的情況較復(fù)雜。

對(duì)n=3，我們研究一些特殊的Markov-Hurwitz 方程的解的結(jié)構(gòu)。

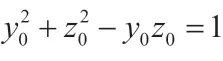
【命題2】Markov-Hurwitz 方程x2+y2+z2=xyz+1 無(wú)正整數(shù)解。

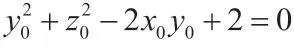
【命題3】Markov-Hurwitz 方程x2+y2+z2=65(xyz+1)的基本解是(1,8,520)與(4,7,1820)。

四、總結(jié)

本文圍繞Markov-Hurwitz 方程展開(kāi)研究，在這個(gè)過(guò)程中提出了一些頗有意義的定理和推論，并給出了自己的證明。