羅經(jīng)方位對準(zhǔn)的收斂時間分析

何東旭，葛磊，張鑫，臧新樂

1 哈爾濱工程大學(xué)自動化學(xué)院，黑龍江哈爾濱150001

2 北京計算機技術(shù)及應(yīng)用研究所，北京100854

0 引 言

羅經(jīng)對準(zhǔn)是慣性導(dǎo)航系統(tǒng)常用的一種初始對準(zhǔn)方法，該方法基于“羅經(jīng)效應(yīng)”原理［1］，應(yīng)用經(jīng)典控制理論，在頻域上設(shè)計羅經(jīng)對準(zhǔn)回路，羅經(jīng)對準(zhǔn)具有設(shè)計參數(shù)少、計算量小、易于實現(xiàn)等優(yōu)點，因此，該方法一直是初始對準(zhǔn)研究方向的熱點。

羅經(jīng)對準(zhǔn)分為水平對準(zhǔn)和方位對準(zhǔn)2 種，一般來講，水平對準(zhǔn)速度快、精度高，難度較小，而方位對準(zhǔn)則是整個對準(zhǔn)過程的關(guān)鍵和難點。李瑤等［2］研究了搖擺狀態(tài)下的捷聯(lián)慣導(dǎo)系統(tǒng)羅經(jīng)法自對準(zhǔn)技術(shù)，設(shè)計優(yōu)化了水平和方位對準(zhǔn)參數(shù)，該方法在不同海情、不同初始姿態(tài)誤差和全方位條件下具有良好的對準(zhǔn)結(jié)果。徐博等［3］研究了航行轉(zhuǎn)臺下的羅經(jīng)回路初始對準(zhǔn)，并基于器件誤差情況等效分析了航行狀態(tài)下的對準(zhǔn)誤差；張娟秀等［4］分析了隨機噪聲對羅經(jīng)方位對準(zhǔn)的影響，并創(chuàng)新性地提出了時域下的分析方法；Gao 等［5］研究了基于姿態(tài)逆向解算的羅經(jīng)對準(zhǔn)方法，并提出陀螺輸出的周期震蕩誤差會使羅經(jīng)方位對準(zhǔn)產(chǎn)生額外的震蕩誤差，且方位誤差會隨切換次數(shù)的增加而放大；He 等［6］提出了基于最優(yōu)模型的時變參數(shù)羅經(jīng)對準(zhǔn)算法，并利用遺傳算法對大方位失準(zhǔn)角條件下的羅經(jīng)對準(zhǔn)參數(shù)進行了優(yōu)化。

盡管研究羅經(jīng)對準(zhǔn)的文獻較多，但是針對羅經(jīng)對準(zhǔn)收斂時間的研究較少。而對于羅經(jīng)對準(zhǔn)來說，收斂時間也是一項較為重要的指標(biāo)，因為在固定的初始對準(zhǔn)時間內(nèi)，既希望系統(tǒng)抗干擾能力強，能將環(huán)境的隨機干擾降低到最小，又要使系統(tǒng)能在初始對準(zhǔn)時間內(nèi)收斂，而這二者往往相互矛盾［6］。嚴(yán)恭敏［7］設(shè)計了四階羅經(jīng)方位對準(zhǔn)控制系統(tǒng)，指出羅經(jīng)方位對準(zhǔn)收斂時間與設(shè)置的二階阻尼震蕩周期有關(guān)，但其只對經(jīng)典的二階系統(tǒng)進行了分析，并以此類比了四階羅經(jīng)方位對準(zhǔn)控制系統(tǒng)，但是采用二階系統(tǒng)的分析方法類比分析四階系統(tǒng)顯然不夠嚴(yán)謹(jǐn)。高鐘毓［8］設(shè)計了三階羅經(jīng)對準(zhǔn)系統(tǒng)，指出在選擇相應(yīng)的參數(shù)時，該系統(tǒng)會在30～50 min收斂，但是并沒有給出具體的分析方法。

基于以上原因，本文將基于通常設(shè)置的四階羅經(jīng)方位對準(zhǔn)系統(tǒng)，分析東向陀螺漂移和初始方位誤差對羅經(jīng)方位對準(zhǔn)收斂時間的影響。提出將方位誤差的頻域響應(yīng)轉(zhuǎn)化成時域響應(yīng)函數(shù)，并在時域上分析收斂時間，巧妙地將方位誤差從頻域轉(zhuǎn)化到時域進行研究，并得出相關(guān)結(jié)論，為羅經(jīng)方位對準(zhǔn)設(shè)置相關(guān)參數(shù)以及控制收斂時間提供理論參考。

1 羅經(jīng)方位對準(zhǔn)原理

羅經(jīng)方位對準(zhǔn)是一種利用“羅經(jīng)效應(yīng)”原理、基于經(jīng)典控制理論的自對準(zhǔn)方法，羅經(jīng)初始對準(zhǔn)分為水平對準(zhǔn)和方位對準(zhǔn)2 個階段，其中方位對準(zhǔn)是在水平對準(zhǔn)的基礎(chǔ)上進行的，這里只簡單介紹羅經(jīng)方位對準(zhǔn)的原理。

羅經(jīng)方位對準(zhǔn)原理如圖1 所示。圖中：R為當(dāng)?shù)刈游缛Π霃剑籹 為拉普拉斯算子；εU為天向陀螺漂移，一般來說，對初始對準(zhǔn)精度的影響較小；ωie為地球自轉(zhuǎn)角速度；L為當(dāng)?shù)氐乩砭暥龋籫為重力加速度；ΔN為北向加速度計偏置；εE為東向陀螺漂移；δVN為北向速度誤差；φx為東向失準(zhǔn)角，φz為方位失準(zhǔn)角；K1，K2為北向水平回路的設(shè)計參數(shù)；K(s) 為羅經(jīng)回路控制環(huán)節(jié)，K(s)=K3[ωiecosL(s+K4)]，其輸入信號為δVN，輸出信號為K(s)δVN，以代替天向控制指令角速度。在羅經(jīng)方位對準(zhǔn)過程中，從φz開始，經(jīng)羅經(jīng)效應(yīng)的各個環(huán)節(jié)，到輸出δVN，再經(jīng)過方位控制環(huán)節(jié)K(s)，調(diào)整輸出φz。

圖1 羅經(jīng)方位對準(zhǔn)原理圖Fig.1 Schematic diagram of compass azimuth alignment

根據(jù)上面羅經(jīng)方位對準(zhǔn)原理圖，可知該四階系統(tǒng)的響應(yīng)為

式中：φx(0)為初始東向失準(zhǔn)角，當(dāng)羅經(jīng)對準(zhǔn)經(jīng)水平調(diào)平后，這一項的值非常小，對羅經(jīng)方位對準(zhǔn)無影響；φz(0)為初始方位角誤差，該誤差會影響羅經(jīng)方位對準(zhǔn)的收斂特性，是需要重點研究的對象；εE會影響方位對準(zhǔn)精度；Δ(s)為羅經(jīng)方位對準(zhǔn)系統(tǒng)的特征方程，且

一般來說，較為成熟的參數(shù)設(shè)置方法是將1 個四階系統(tǒng)變成2 個相同的二階系統(tǒng)的串聯(lián)形式，且該系統(tǒng)的特征根有如下形式［2］：

因此，在羅經(jīng)方位對準(zhǔn)中，只需設(shè)定好Td的值，其它參數(shù)也就相應(yīng)確定［10］。實際上，參數(shù)Td的設(shè)置與初始對準(zhǔn)時間、初始方位誤差、慣性器件的隨機漂移以及載體晃動干擾情況都有關(guān)，也是羅經(jīng)方位對準(zhǔn)中需重點研究的方向，不過在本文中，不討論參數(shù)Td的設(shè)置問題。

從φz的頻域響應(yīng)函數(shù)可知，φz的輸出受5 個參數(shù)的影響，但由相關(guān)文獻可知，ΔN，φx(0)和εU對羅經(jīng)方位對準(zhǔn)的影響也較小，且其數(shù)量級都很小，所以這里不考慮這3 個參數(shù)對收斂速度的影響，本文重點分析東向陀螺漂移εE和初始方位角誤差φz(0)對羅經(jīng)方位對準(zhǔn)收斂時間的影響。

2 羅經(jīng)方位對準(zhǔn)收斂時間分析

2.1 羅經(jīng)方位對準(zhǔn)收斂判定

一般在自動控制理論中，通常被控制參數(shù)進入到某個誤差帶中，則認(rèn)為系統(tǒng)進入穩(wěn)態(tài)過程，即系統(tǒng)收斂。并且在自動控制理論中，一般取誤差帶為穩(wěn)態(tài)值的2%或5%。但在研究羅經(jīng)方位對準(zhǔn)時不宜這樣選取，因為初始方位誤差對羅經(jīng)方位對準(zhǔn)影響的穩(wěn)態(tài)值為0，無法以穩(wěn)態(tài)值的百分比取誤差帶；另外，在初始對準(zhǔn)時，通常需要根據(jù)慣性器件精度及對方位角精度的要求，綜合考慮方位收斂的判據(jù)，因此，本文以方位角進入到以角度為單位的誤差帶作為羅經(jīng)方位對準(zhǔn)收斂的判據(jù)。

在本文中，限定陀螺零偏穩(wěn)定性在0.05（°）/h以內(nèi)，根據(jù)初始對準(zhǔn)誤差公式可知，在北緯53 °以內(nèi)，其初始對準(zhǔn)誤差在0.35 °以內(nèi)，再綜合考慮隨機誤差對初始對準(zhǔn)的影響，本文取0.01 °的誤差帶，這對于中等慣性器件精度的初始對準(zhǔn)來說，可以認(rèn)為已經(jīng)收斂。當(dāng)然，在實際應(yīng)用中，可根據(jù)實際應(yīng)用環(huán)境、慣性器件精度及對準(zhǔn)精度的要求，對收斂判據(jù)進行調(diào)整。如果陀螺零偏穩(wěn)定性在0.001（°）/h 的量級，則可將誤差帶提高至0.005 °，如果陀螺零偏穩(wěn)定性在0.1（°）/h 量級，則可將誤差帶放寬至0.02°或0.03°。

2.2 陀螺常值漂移對收斂時間的影響

由第1 節(jié)可知，與東向陀螺漂移有關(guān)的系統(tǒng)響應(yīng)項為

為了考察該響應(yīng)的時間特性，將其頻域響應(yīng)轉(zhuǎn)化成時域響應(yīng)函數(shù)Td，對φz1(s)求取拉普拉斯反變換，則有

按照第1 節(jié)相關(guān)參數(shù)取值，有σ=ωd=2πTd，gK3=4σ4，因ωd與σ只是在數(shù)值上相等，其物理含義并不相同，因此，涉及到正余弦運算的ωd不用σ替換。式（5）可簡化為

由上式可以看出，φz1(t)收斂于-εEωiecosL，這與相關(guān)文獻中東向陀螺漂移對初始對準(zhǔn)的影響的相關(guān)公式吻合［11］，而這里要考慮的是φz1(t)何時收斂。

由于在本文中限定陀螺零偏穩(wěn)定性小于0.05（°）/h，則陀螺常值漂移一般小于0.05（°）/h，再取緯度為53°，則此時有

考慮上式中的4 個衰減震蕩誤差項，有

式中，φ1～φ3為相位角。

取0.01°誤差帶判定羅經(jīng)方位對準(zhǔn)收斂，則有

則 可 解 得σt=5.57 ，從 而 有t=5.57σ=5.57Td2π ≈0.9Td，即經(jīng)過約0.9 個阻尼震蕩周期，羅經(jīng)方位對準(zhǔn)收斂到0.01°的誤差帶。

因此，可以得出結(jié)論：東向陀螺漂移對羅經(jīng)方位對準(zhǔn)造成的影響至多可在0.9 個阻尼震蕩周期內(nèi)收斂。本文的分析過于保守，隨著陀螺精度的提高，其常值漂移會減小，則其收斂時間將會更短。表1 列出幾個典型陀螺常值漂移條件下的收斂時間。

表1 不同陀螺常值漂移的收斂時間Table 1 Convergence time of different gyros constant drift

從表1 可以看出，羅經(jīng)方位對準(zhǔn)的收斂時間與設(shè)置的二階阻尼震蕩周期和陀螺常值漂移有關(guān)，當(dāng)陀螺常值漂移確定時，收斂時間與二階阻尼震蕩周期存在固定的比例關(guān)系；而當(dāng)二階阻尼震蕩周期確定時，陀螺常值漂移越大，則收斂時間越長，陀螺常值漂移越小，則收斂時間越短。

還有一點要說明，在進行收斂時間的理論計算時，由于采用了不等式放大，故實際收斂時間往往會小于所計算的理論時間，因此，此處的收斂時間較為保守，是系統(tǒng)穩(wěn)定所需的最長時間。

2.3 初始方位誤差對收斂時間的影響

由第1 節(jié)可知，與初始方位誤差有關(guān)的系統(tǒng)響應(yīng)項為

按照第1 節(jié)的相關(guān)參數(shù)取值，則有

對其求拉普拉斯反變換，得到時域響應(yīng)函數(shù)：

由于在參數(shù)設(shè)置中有ωd=σ，故有

從上式可以看出，φz2(t) 最終收斂于0，而本文研究的目標(biāo)是其何時收斂。

由于

因此有

以0.01°的誤差帶為判定初始對準(zhǔn)收斂的判據(jù)，則有

根據(jù)上式可知，φz2(t)的大小與初始方位誤差φz(0)成比例關(guān)系，因此其收斂時間與初始方位角誤差的大小有關(guān)。并且從上式還可以簡單看出，φz(0)越大，收斂時間越長。

一般來說，在進行羅經(jīng)對準(zhǔn)前，需要進行粗對準(zhǔn)［12］，以保證羅經(jīng)方位對準(zhǔn)誤差模型的線性特性。當(dāng)初始方位角誤差在5 °以內(nèi)時，慣導(dǎo)誤差模型具有較好的線性特性，利用羅經(jīng)方位對準(zhǔn)進行初始對準(zhǔn)效果較好；當(dāng)初始方位角誤差大于5 °時，慣導(dǎo)誤差模型的線性度逐漸變差，羅經(jīng)方位對準(zhǔn)的性能就會變差。因此，在實際應(yīng)用中，粗對準(zhǔn)的誤差一般要控制在5 °以內(nèi)，而本節(jié)也只研究初始方位誤差在5 °以內(nèi)的羅經(jīng)方位對準(zhǔn)收斂時間。并且，由于水面艦艇上的羅經(jīng)裝備在實際使用中初始方位誤差不會太大，一般會在1°以內(nèi)，因此本文重點列出初始方位誤差在1°以內(nèi)時羅經(jīng)方位對準(zhǔn)的收斂時間。根據(jù)式（16），列出了在一些典型初始誤差值條件下羅經(jīng)方位對準(zhǔn)的收斂時間，如表2所示。

表2 不同初始方位誤差的收斂時間Table 2 Convergence time of different initial azimuth misalignment

從表2 可以看出，羅經(jīng)方位對準(zhǔn)的收斂時間與設(shè)置的二階阻尼震蕩周期和初始方位誤差有關(guān)，當(dāng)初始方位誤差確定時，收斂時間與二階阻尼震蕩周期存在固定的比例關(guān)系；而當(dāng)二階阻尼震蕩周期確定時，初始方位誤差越大，則羅經(jīng)方位對準(zhǔn)的收斂時間越長，初始方位誤差越小，則羅經(jīng)方位對準(zhǔn)收斂時間越短。

與2.2 節(jié)同理，表2 所列的收斂時間也較為保守，一般情況下，實際收斂時間要小于理論計算出的時間。

2.4 兩種誤差共存時對收斂時間的影響

在慣導(dǎo)實際的初始對準(zhǔn)中，陀螺常值漂移和初始方位誤差是同時存在的，因此，分析2 種誤差同時存在，對收斂時間的影響很有必要，對實際應(yīng)用中羅經(jīng)方位對準(zhǔn)的參數(shù)設(shè)置具有重要的理論指導(dǎo)意義。

陀螺常值漂移和初始方位誤差相互獨立，則根據(jù)自動控制理論可知，二者經(jīng)羅經(jīng)方位對準(zhǔn)傳遞函數(shù)得到的響應(yīng)可以線性疊加，因此當(dāng)2 種誤差同時存在時，羅經(jīng)方位對準(zhǔn)誤差的響應(yīng)函數(shù)為

從上式可以看出，當(dāng)2 項誤差同時存在時，φz3(t)收斂于-εEωiecosL，誤差衰減震蕩項為

因此有

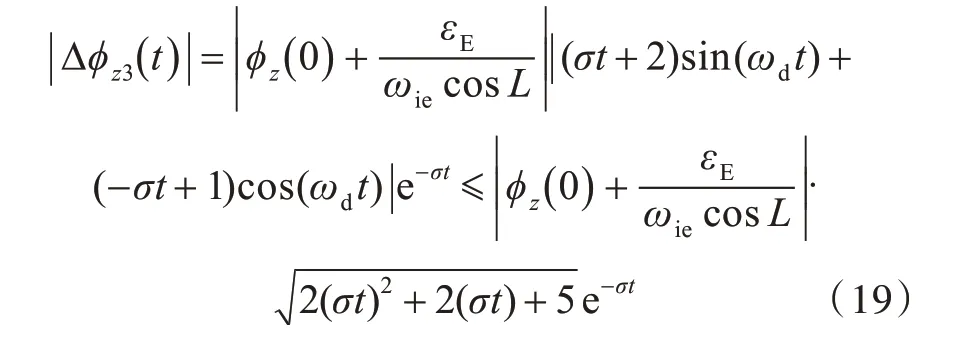
以0.01 °的誤差帶為判定初始對準(zhǔn)收斂的判據(jù)，則有

表3 列出了一些典型初始方位誤差和陀螺常值漂移下的收斂時間。

表3 典型初始方位誤差和陀螺常值漂移下的收斂時間Table 3 Typical convergence time of different initial azimuth misalignment and gyro constant drift

對比表2 和表3 可以看出，相對于初始方位誤差，陀螺常值漂移對收斂時間影響不大，主要影響收斂時間的因素是初始方位誤差。

因此，可以得出結(jié)論：當(dāng)陀螺常值漂移和初始方位誤差同時存在時，影響羅經(jīng)方位對準(zhǔn)的主要因素為初始方位誤差；當(dāng)陀螺常值漂移在0.05（°）/h以內(nèi)，初始方位誤差在5 °以內(nèi)時，羅經(jīng)方位對準(zhǔn)會在至多1.41Td時間內(nèi)收斂，初始方位誤差越小，收斂時間也會越短。

3 仿真驗證

在本節(jié)仿真中，首先分別驗證陀螺常值漂移和初始方位誤差對羅經(jīng)方位對準(zhǔn)收斂時間的影響，再驗證二者共同存在時對羅經(jīng)方位對準(zhǔn)收斂時間的影響，主要驗證這3 種條件下羅經(jīng)方位對準(zhǔn)收斂時間是否與理論分析相吻合。

3.1 陀螺常值漂移對收斂時間影響仿真

假設(shè)參考坐標(biāo)系為東北天坐標(biāo)系，當(dāng)?shù)氐乩砭暥葹?3 °，慣導(dǎo)只有X 軸陀螺具有0.05（°）/h 的常值漂移，慣導(dǎo)的姿態(tài)為0 °，0 °，0 °，初始姿態(tài)誤差皆為0°，設(shè)置Td分別等于200，300，400 和500 s，仿真時間為600 s，得到初始對準(zhǔn)誤差收斂曲線如圖2 所示。

圖2 陀螺常值漂移0.05（°）/h 時不同Td下的誤差收斂曲線Fig.2 Convergence curves in different Td with 0.05（°）/h gyros constant drift

由初始對準(zhǔn)相關(guān)理論可知，此時初始對準(zhǔn)誤差穩(wěn)定值為-0.316 5°。因此，結(jié)合上圖和本文0.01°誤差帶的定義可知，初始對準(zhǔn)誤差曲線在最后一次穿過-0.326 5 °時，即可認(rèn)為羅經(jīng)方位對準(zhǔn)收斂，此時，對于不同的Td，收斂時間分別如表4所示。

表4 陀螺漂移0.05（°）/h 時不同Td的收斂時間Table 4 Convergence time of different Td with 0.05（°）/h gyros constant drift

從表4 可以看出，對于不同的Td，雖然收斂時間不同，但是收斂時間與Td的比值與理論分析結(jié)果吻合較好，驗證了所提出分析方法的有效性。

限于篇幅，這里不再畫出其它陀螺漂移時的收斂曲線，只通過表5 列出陀螺漂移取0.01，0.02，0.03 和0.04（°）/h，Td取200，300，400 和500 s 時的收斂時間及收斂時間與Td的比值。

表5 不同Td和陀螺常值漂移下的收斂時間Table 5 Convergence time of different Td and different gyros constant drift

從表5 可以看出，當(dāng)陀螺漂移在0.02（°）/h 以上時，與理論計算結(jié)果吻合較好，而在0.02 和0.01（°）/h 時，實際收斂時間要小于理論收斂時間，其原因是在理論推導(dǎo)過程中采用了不等式的放大，使得理論計算的收斂時間過于保守，但從總體來說，本文的分析方法是有效的。

3.2 初始方位誤差對收斂時間影響仿真

假設(shè)慣性器件無誤差，初始方位誤差為5 °，設(shè)置Td分 別 為200，300 ，400 和500 s，仿 真 時間 為1 000 s，姿態(tài)為0 °，0 °，0 °，仿真結(jié)果如圖3和表6 所示。

圖3 初始方位誤差5°時不同Td值下的收斂曲線Fig.3 Convergence curves in different Td with 5°initial azimuth misalignment

表6 初始方位誤差5°時不同Td的收斂時間Table 6 Convergence time of different Td with 5°initial azimuth misalignment

從表6 可以看出，對于不同的Td，雖然收斂時間不同，但是收斂時間和Td的比值與理論分析結(jié)果吻合較好，驗證了所提出分析方法的有效性。

限于篇幅，本文不再畫出其它陀螺漂移時的收斂曲線，只通過表7 列出一些典型初始方位誤差條件下的收斂時間。特別考慮了水面艦艇上羅經(jīng)裝備初始方位誤差一般不超過1°的實際使用情況，也重點列出了初始方位誤差在1°以內(nèi)時對羅經(jīng)方位對準(zhǔn)收斂時間的影響。因此表7 列出了初始方位誤差為4 °，3 °，2 °，1 °，0.8°，0.6°，0.4°和0.2°，Td取200，300 ，400 和500 s 時的收斂時間及其與Td的比值。

表7 不同Td和初始方位誤差下的收斂時間Table 7 Convergence time of different Td and different initial azimuth misalignment

從表中可以看出，當(dāng)初始方位誤差大于2 °時與理論計算結(jié)果較為吻合，而當(dāng)初始方位誤差小于2°時，實際收斂時間要小于理論計算時間。這一現(xiàn)象是由于在理論分析中采用了不等式的放大而造成，但總體來說，本文所提出的分析方法有效。

3.3 兩種誤差共存時對收斂時間影響仿真

假設(shè)慣性器件無誤差，初始方位誤差為5 °，陀螺常值漂移為0.05（°）/h，設(shè)置Td分別為200 ，300，400 和500 s，仿真時間為1 000 s，姿態(tài)為0 °，0°，0°，仿真結(jié)果如圖4 和表8 所示。

限于篇幅，這里不再畫出其它條件下的收斂曲線，只通過表9 列出初始方位誤差取4 °，3 °，2 °，1 °和0.5 °，陀螺常值漂移取0.05（°）/h，Td取200，300，400 和500 s 時的收斂時間及其與Td的比值，以驗證理論分析的有效性。

圖4 不同Td值下的收斂曲線Fig.4 Convergence curves in different Td

表8 陀螺漂移0.05（°）/h 和初始方位誤差5°時不同Td的收斂時間Table 8 Convergence time of different Td with 0.05（°）/h gyro drift and 5°initial azimuth misalignment

表9 陀螺漂移0.05（°）/h 時不同Td和初始方位誤差下的收斂時間Table 9 Convergence time of different Td and different initial azimuth misalignment with 0.05（°）/h gyro drift

對比表9 可以看出，當(dāng)陀螺漂移設(shè)置到較大值0.05（°）/h 時，不同初始方位誤差條件下的收斂時間差別不大，且都與Td時間相關(guān)，成比例關(guān)系，進而驗證了本文所提分析方法的正確性。

4 結(jié) 論

羅經(jīng)方位對準(zhǔn)的精確性和快速性往往互相矛盾，在固定的初始對準(zhǔn)時間內(nèi)，既希望盡可能多地濾掉隨機干擾，又要求羅經(jīng)方位對準(zhǔn)收斂，因此，分析羅經(jīng)方位對準(zhǔn)的收斂時間特性就顯得十分有必要。本文在求得羅經(jīng)方位對準(zhǔn)傳遞函數(shù)的東向陀螺漂移和初始方位誤差的頻域響應(yīng)基礎(chǔ)上，通過拉普拉斯反變換將其轉(zhuǎn)化成時域響應(yīng)函數(shù)，在時域上針對東向陀螺漂移和初始方位誤差對羅經(jīng)方位對準(zhǔn)收斂時間的影響進行了分析。通過分析，主要得出以下結(jié)論：

1）通過分析時域響應(yīng)函數(shù)，表明羅經(jīng)方位對準(zhǔn)的收斂時間與陀螺常值漂移、初始方位誤差和設(shè)置的二階阻尼震蕩周期Td有關(guān)。

2）當(dāng)以0.01 °誤差帶為收斂判據(jù)時，由陀螺常值漂移引起的方位角誤差會在至多0.9Td時間內(nèi)收斂，由初始方位誤差引起的方位角誤差會在至多1.39Td時間內(nèi)收斂。

3）當(dāng)二者共同作用時，對收斂時間起主要作用的是初始方位誤差，陀螺常值漂移對收斂時間的影響較小，基本可忽略不計。

本文所提出的方法為設(shè)置羅經(jīng)方位對準(zhǔn)相關(guān)參數(shù)，控制羅經(jīng)方位對準(zhǔn)收斂時間提供了理論依據(jù)。