校政共建高校與區域發展互惠共贏
吳鐘輝 梁家榮 羅玉梅 廖曼琪

摘 要:本文立足于校政合作模式下,實證研究高等教育發展與區域發展互動雙贏的關系。首先,通過文獻研究梳理,從高校與地方政府協同辦學的理論框架入手,探究校政合作的內涵和現狀,闡述校政合作辦學的意義和效果。其次,基于珠海市發展狀況,以地方政府與高校協同辦學作為成功案例,從教育的投入、人力資本存量兩因素實證檢驗高等教育對區域經濟發展、社會發展、自主創新發展的影響。另一方面,再通過區域發展對高等教育必要性的闡述,協整檢驗兩者間存在的良性關系,進一步論證高等教育發展與區域發展存在互動雙贏的效果。最后,根據定性分析和實證分析結果,提出校政合作模式下,高等教育與區域發展互動雙贏良性共進的有效建議。
關鍵詞:區域發展;高等教育;校政合作;實證研究
一、文獻綜述
(一)研究背景
1.知識經濟的到來
知識是高等教育的邏輯起點,隨著信息時代的到來,經濟、知識與信息一體化,科學技術出現革命性發展,使得知識經濟已成為一種新興的社會形態。高校是經濟發展的動力源,以知識決策為導向的經濟,指明了經濟和社會發展的方向,因此,高等教育產生的知識已然成為促進時代進步、區域經濟蓬勃發展的高效催化劑。
2.高校與區域發展的需求
隨著高等教育大眾化趨勢的發展,各個地區為了提高自身的市場競爭力,對人才培養、人才要求程度也逐漸提高。一方面,高校在擴大辦學規模的同時,對土地資源的利用,遇到的瓶頸壓力也不斷增加。因此,校政合作作為有效辦學方式之一,高校與地方政府協同辦學的合作模式在社會發展中慢慢產生。另一方面,區域經濟作為內部因素和外部因素的共生體,新經濟的變革更需要教育和知識帶來的科技創新和進步,實現高等教育區域化,也將滿足實現地區經濟產業結構轉型的戰略需求。可見,高等教育在區域協調發展和規劃方面起到了至關重要的作用。
(二)國內外研究概述
美國學者亨利埃茨科威茲(Henry)提出了“大學——產業——政府”關系的三螺旋理論,通過大學、產業、政府這三個創新單元的聯動來推動知識創新、傳播和轉化生產力,用三者相互作用的合力來推動創新形成螺旋上升。隨著經濟不斷發展,社會職能轉變,1903年,英國率先采用了合作教育下的“工讀交替”模式,之后德國、澳大利亞、美國相繼建立了產學研教育制度,政府為高校與企業,高校與地區的“產學研合作”發揮了聯結的紐帶作用。
我國學者龍獻忠與張躍華(2006)指出創新性人才培養需要政府、企業、大學、社會的共同合作來完成;周清和車士義(2009)在三螺旋理論的基礎上,實證分析高等院校與區域經濟存在互動雙贏、良性發展的關系;學者劉金存(2010)提出“校政共建”的概念。在實踐層面上,2006年,江蘇科技大學與張家港市政府合作辦學,建立江蘇科技大學張家港校區,左婧(2015)以南寧學院和廣西壯族自治區質量技術監督局合作為例,深入分析了校政合作實踐中教育發展和社會經濟發展的關系。
(三)文獻簡評
總而言之,國內高校與地方政府協同辦學,是在經濟不斷發展,社會管理職能轉變,市場競爭加劇的形勢下所推出的合作模式,是在高等教育大眾化的趨勢下所逐漸形成的一種合作模式,大多數的理論研究都建立在校政合作的實踐層面上,高校與地方政府存在一種合作關系,地方政府具有主導協調作用,能夠發揮其行業職能,引導和推動高校與企業、高校與地區聯合發展。
二、研究內容
首先,本文基于珠海市發展狀況,以地方政府與高校協同辦學作為成功案例,從教育的投入、人力資本存量兩因素實證檢驗高等教育對區域經濟發展、社會發展、自主創新發展的影響。另一方面,再通過區域發展對高等教育必要性的闡述,協整檢驗兩者間存在的良性關系,進一步論證高等教育發展與區域發展存在互動雙贏的效果。最后,根據定性分析和實證分析結果,提出校政合作模式下,高等教育與區域發展互動雙贏良性共進的有效建議。
三、實證分析
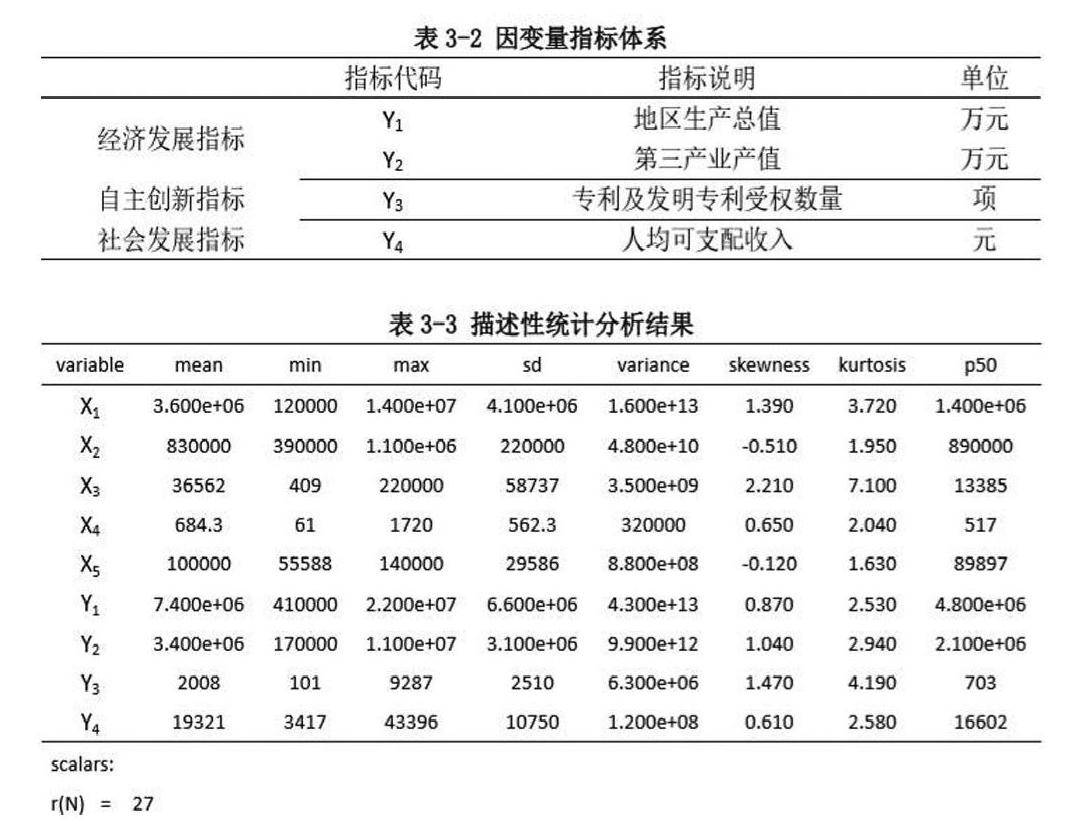
(一)描述性統計分析
本文選取了1990年到2016年的27年的數據為樣本,如表3-1和表3-2所示,對5個自變量,4個因變量進行描述性統計。描述性統計分析結果如表3-3所示,由統計分析的結果知,10個變量的均值與標準差之間相差不大,說明這些變量不存在極端異常值,可以進行后續的模型建立。根據收集到的變量數據,可以得到1990-2016年自變量及因變量的趨勢,x1-x5變量均呈現為穩步上升的變化趨勢,特別是在高等院校出現并完善之后(2004到2016年),五個變量的增量不斷上升。因變量y1-y4呈增長趨勢,尤其是在2004年以后。這說明了在有高等教育的情況下,經濟發展能力、自主創新能力和社會發展能力均有進步。說明了高等教育對經濟發展方式的轉變有一定的促進作用。
(二)線性回歸分析
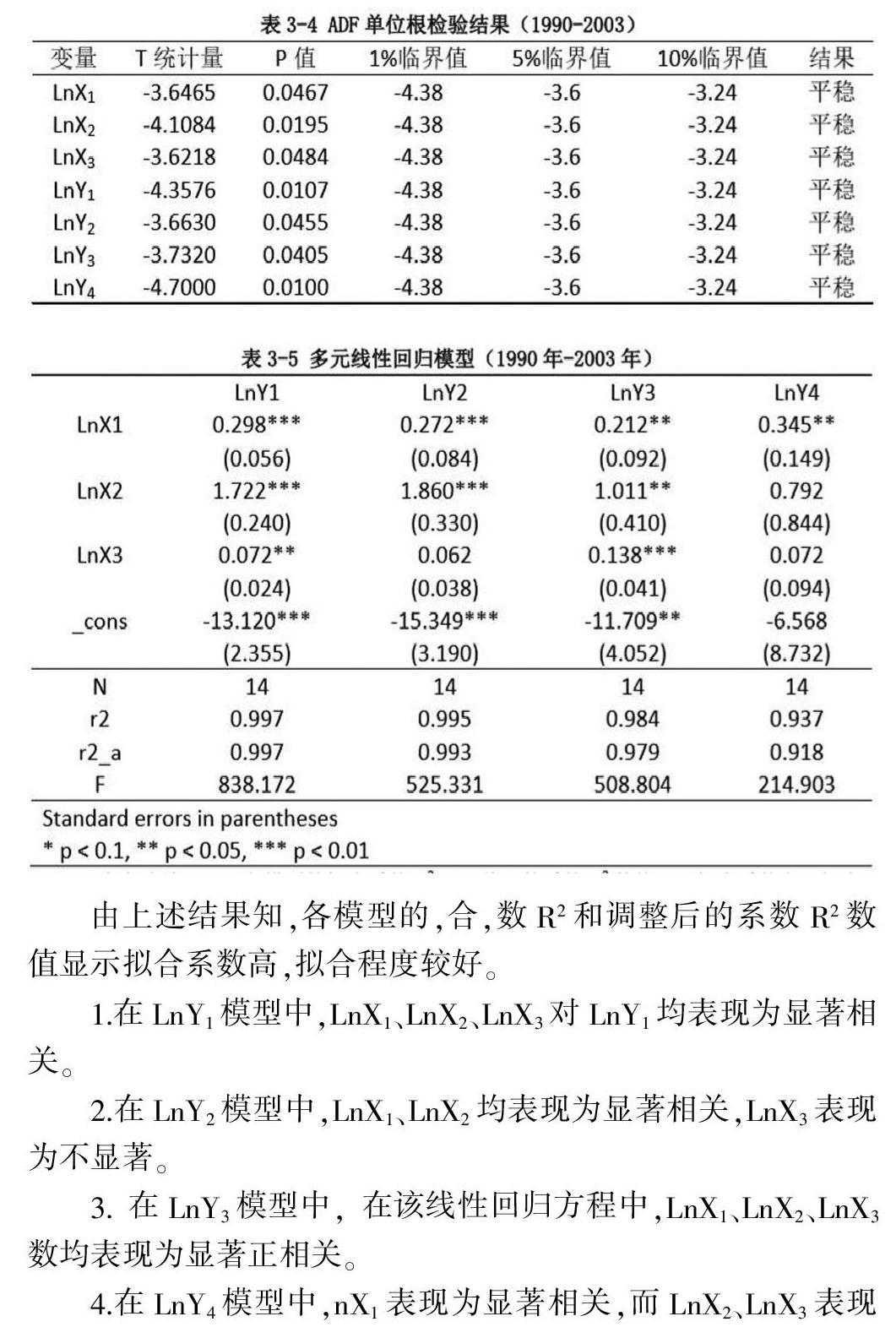
通過上述變量分析,首先進行ADF單位根檢驗,結果如表3-4所示,進而構建多元線性回歸模型為:
其中,c為常數項,α1,α2,α3為回歸系數,ε誤差項。
由上述結果知,各模型的,合,數R2和調整后的系數R2數值顯示擬合系數高,擬合程度較好。
1.在LnY1模型中,LnX1、LnX2、LnX3對LnY1均表現為顯著相關。
2.在LnY2模型中,LnX1、LnX2均表現為顯著相關,LnX3表現為不顯著。
3.在LnY3模型中,在該線性回歸方程中,LnX1、LnX2、LnX3數均表現為顯著正相關。
4.在LnY4模型中,nX1表現為顯著相關,而LnX2、LnX3表現為不顯著相關。
比較分析第二個時間序列區間,同樣地,首先進行ADF單位根檢驗,結果如表3-6所示,進而構建多元線性回歸模型:其中,c為常數項,α1,α2,α3,α4,α5為回歸系數,ε誤差項。

