觸發學生“高峰體驗”的教學策略

翟運勝

【摘? ?要】“高峰體驗”是人在學習中的一種內心體驗，它是激發學習者興趣的本原力量。教師要想觸發學生的“高峰體驗”，在數學課堂上可以通過運用“幫助學生樹立自信，制造認知沖突，引導學生自行解決問題，引領學生深度理解所學內容，讓學生專注思考”等教學策略，使學生感受數學學習的成功與幸福，樹立學習信心，形成品格。

【關鍵詞】高峰體驗;深度學習;教學策略

“高峰體驗”（peak experience）是美國心理學家馬斯洛“自我實現論”中的重要概念，是一種能夠讓人在一剎那之間覺得無所遺憾、一切美好圓滿的感覺。他發現人偶爾會出現“高峰體驗”，如經長時間冥思苦想的問題瞬間得到解決，或出現頓悟，會感受到一種發自心靈的顫栗、欣快、滿足、超然的情緒體驗，使心靈得到升華，達到最大程度的自我認同。學生在數學學習中的“高峰體驗”，是他們樹立學習信心，形成學習興趣，產生對數學親近感的重要力量之源，也是促進他們形成數學必備品格的重要方式。

數學學習中的“高峰體驗”是一種沉浸性的學習體驗，有助于學生擺脫功利性的學習目的，為探求新知攻克難題感覺“有意思”而愿意付出更多的辛勞與努力。數學學習的“高峰體驗”可滿足學生自我實現的心理需求，使學生的學習意志更加趨于穩定，從而沉淀成一種學習的必備品格。

數學教師應當琢磨如何讓學生經歷“高峰體驗”，以促進學生健康人格的形成，產生對數學的美好情感，從而對數學的未知世界產生好奇心理，形成和發展創造力。

一、幫助學生樹立自信

通過對學習積極主動、對未知充滿興趣、數學成績優秀的學生的觀察，發現他們身上出現學習“高峰體驗”的次數較多，頻次較高。那么，是不是只有成績優秀的學生身上才會出現這種學習的“高峰體驗”呢？不是的，各種學習水平的學生身上都有可能出現，只是有出現次數與頻率的差別而已。因為對于每個學生來講，“在他的內心深處，都有一種根深蒂固的需要，就是希望自己成為一個開發者、研究者、探索者”。 教師要引導學生相信自己的潛能，不斷地加以喚醒與激勵，使之形成一種成長的心態，奠定產生“高峰體驗”的基石。

二、設置認知沖突，激發學生的探究欲

認知沖突是指學生已有的認知結構與當前的學習情境之間存在的暫時性矛盾，通常表現為學生已有的知識經驗與新知之間存在某種差距而導致的心理失衡。學生的數學學習過程是一個不斷產生、化解和發展內心沖突的過程。認知沖突可以使學生處于“憤悱”的心理狀態，促進知識的重組與優化，在這種狀態下引導、點撥與教授學生，使學生經歷思維沖浪的過程，激發學生的探究欲，引起豁然開朗的“高峰體驗”。

如教學蘇教版五年級上冊“釘子板上的多邊形”，在規律的探求階段，可以通過制造如下認知沖突，觸發學生的“高峰體驗”。

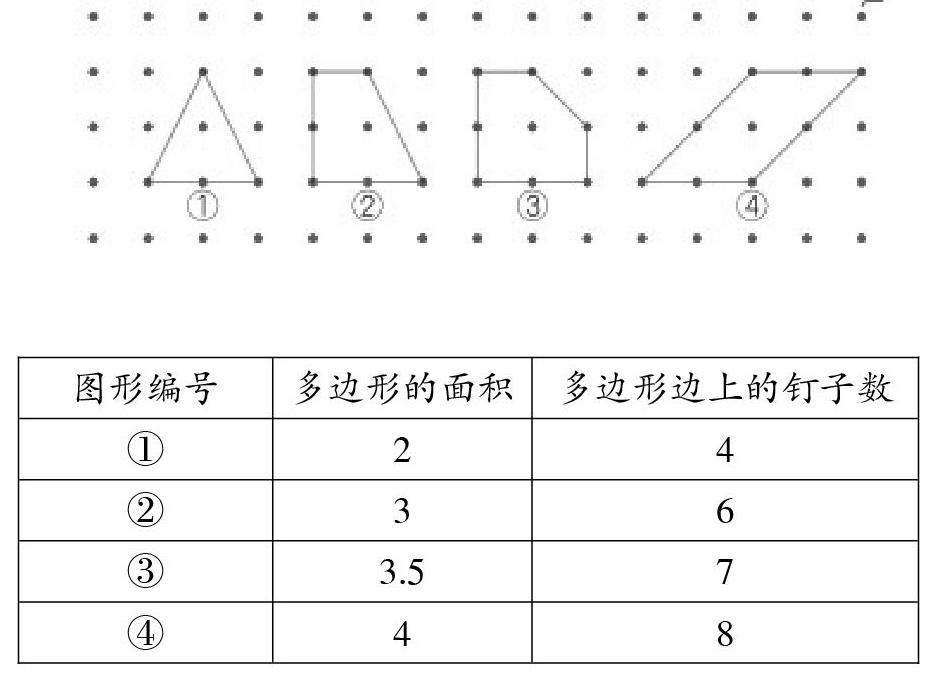
師：請同學們用算與數的方法把這四個多邊形的面積求出來，并把它們邊上的釘子數也數出來，填在下面的表格中。你有什么發現？

學生獨立填表后，然后匯報，教師出示結果。

師：觀察這四組數據，你們有什么發現？

生：多邊形的面積是多邊形邊上釘子數的一半。

師：如果我們用S表示多邊形的面積，n表示邊上的釘子數。S等于什么呢？

生：S=n÷2。

師：這四幅圖都是老師提供的，得出這個結論對不對呢？我們還要來驗證一下，請你在釘子板上任意畫一個多邊形，驗證一下這個結論對不對。

學生在嘗試畫圖后，議論紛紛，表示有不同的意見。師出示學生畫的多邊形。

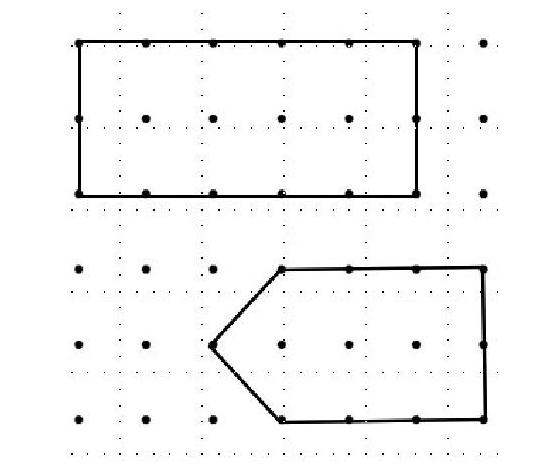
生：上面這個四邊形的面積是10，而它邊上的釘子數是14，邊上的釘子數不是它面積的2倍。

生：下面這個圖形的面積是7，而它邊上的釘子數是10，邊上的釘子數也不是它面積的2倍。

師：這是什么原因呢？難道是我們發現的規律有問題嗎？這兩個圖形與前面四個圖形有什么不同呢？

生：前面四幅圖中多邊形的內部都只有1枚釘子。

學生發現了規律，教師引導學生利用這個規律檢測自己畫的長方形，學生發現規律在此處“失效”了，于是急切地想知道：為什么自己畫出的圖形不存在這種規律？問題出在哪里？這是一個培養學生觀察與分析能力的好時機，教學中教師不能越位，應當舍得花時間，等待學生自己發現“這兩個圖形與前面的四個圖形有什么不同”，對于找到問題答案的學生要給予表揚與激勵。當學生暫時不能發現時，教師也不要忙于點撥引導、包辦代替。教學實踐表明，此處只要教師退一步慢一步，一般情況下學生都能發現自己畫出的平面圖形內部有2個及2個以上的釘子數。當學生自己發現問題所在，其喜悅之情溢于言表。從發現規律到否定規律再到重建規律，使學生經歷沖突、思維激蕩的過程，最終引發“高峰體驗”，享受峰回路轉的美妙之感。

三、引導學生自行解決問題

孩子是天生的學習者，但數學的抽象讓許多孩子產生畏難情緒，不愿意去接近，沒有興趣思考。數學教師要善于對教材進行適度改編，把“學術形態”的數學轉化為學習形態的數學，把“冰冷的美麗”轉變為“火熱的思考”。

蘇教版五年級下冊《因數與倍數》中的“你知道嗎”欄目提供了一個有關“完美數”的閱讀素材，教學時如果把完美數僅當成一個材料提供給學生，讓學生讀一讀，不會激起學生太多的興趣。教師可以這樣進行引導：

師：6的因數有哪些呢？ 6的因數有1，2，3，6。我們觀察這四個因數，你會有什么發現呢？

生：是的，1+2+3=6。

師：一個數的因數，去掉它本身，其余的數相加的和就等于這個數，這樣的數是十分完美的，我們稱之為完美數。有一位同學的學號，也是完美數，你能找到這個數嗎？

學生興趣盎然地開始嘗試尋找。有學生興奮地說：“我找到了！28是完美數！”

師：還有嗎？請大家繼續找。

教學中不在于學生能否找到，而在于學生是否愿意去找。找的過程其實是訓練找一個數因數的過程，而這訓練的過程是學生主動參與的。通過把閱讀材料變為嘗試尋找一個完美數，較容易激發學生產生“高峰體驗”。

四、引領學生深度理解所學內容

在深度學習的教學設計中，要重點體現對學科知識的深刻理解，適時延伸教材，將學生的思維引向深處。

如在教學2，5和3的倍數特征時，不要在總結出特征后就進入相應的判斷練習，而應組織學生進行對比思考：為什么2的倍數特征個位是0，2，4，6，8呢？為什么5的倍數特征個位是0，5呢？為什么只要看個位就可以了呢？十位、百位、千位為什么可以不看？對比3的倍數特征與2，5的倍數特征，你們有什么想問的嗎？為什么3的倍數要看數位上的數字之和呢？引導學生進行深度思考：2的倍數與5的倍數，學生加一加或者乘一乘就會發現2的倍數與5的倍數的個位只可能是這些數字，通過推理能夠得出幾個十、幾個百、幾個千一定是2和5的倍數，所以十位、百位、千位等數位上的數字可以“放棄”了。而幾個十、幾個百、幾個千去除以3以后，不能正好除盡，余下來的數要合在一起繼續再除以3，所以3的倍數特征要看各位上的數字之和。

再如教學量角時，應當讓學生理解量角的本質是“數角里面有多少個1°”，在量角器上就是求與角的兩條邊重合的刻度線的度數差，因此與邊重合的刻度線不一定要零刻度線。深度理解能夠讓學生經歷創造性解決問題的過程，引發學生的“高峰體驗”。

五、讓學生專注思考，漸入佳境

小學數學課堂中缺少較長時間的靜謐思考，這主要是由學生的年齡特點決定的，但是不代表教師不需要在教學中做這方面的努力。結合一些教學內容，讓學生靜下心來思考，想好了再回答，想好了再操作，想好了再討論，避免思維淺層化，避免片面追求速度效率，讓學生更加專注、有效、深入地學習。

專注是學習力中具有凝聚效力的品質。要讓學生專注數學學習，首先應從容易的入手，能很快地思考出來，其次是有點小難度。隨著思考的深入，不斷有新的挑戰吸引學生，使學生欲罷不能。學生經歷靜思默想，產生“原來如此”“我知道了”的頓悟與豁然，專注是觸發學生“高峰體驗”的重要策略。學生入迷了，距離觸發“高峰體驗”也就不遠了。

曲折的學習過程，是“高峰體驗”的前奏，“高峰體驗”是“風雨之后的彩虹”。尼采有這樣一句名言：誰終將聲震人間，必長久深自緘默;誰終將點燃閃電，必長久如云漂泊。“高峰體驗”是對一個人艱苦智力勞動的獎賞。

（江蘇省蘇州工業園區方洲小學 215028）